冀教版数学八年级上册 小专题(六)构造全等三角形的方法课件(共14张PPT)
文档属性
| 名称 | 冀教版数学八年级上册 小专题(六)构造全等三角形的方法课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 09:43:48 | ||
图片预览





文档简介
(共14张PPT)
人
①方法一:翻折法
1.如图,点C,E分别为△ABD的边BD,AB上两点,且
AE=AD,CE=CD,∠D=70°,∠ECD=150°,求∠B
的度数.
解:连接AC,
.AE=AD,CE=CD,AC=AC,
△ACE≌△ACD,
E
..∠AEC=∠D=70°,
B
/BCE=180°-∠ECD=30°,
∠B=∠AEC-∠BCE=40°.
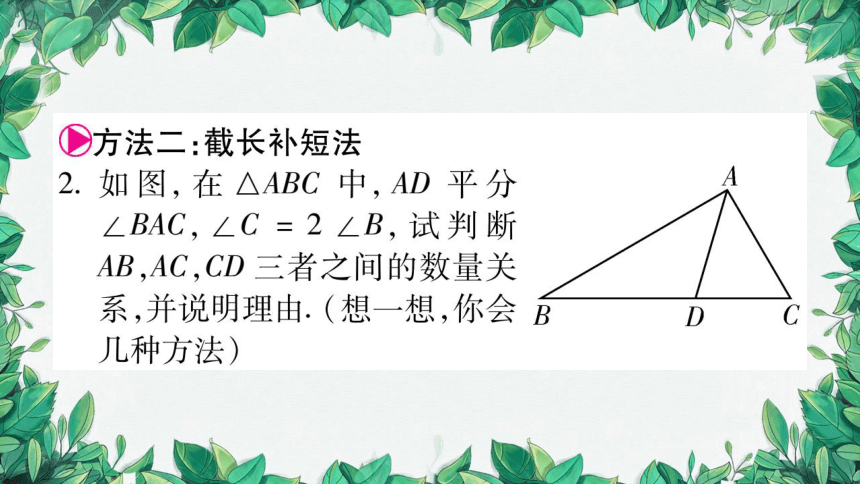
①方法二:截长补短法
2.如图,在△ABC中,AD平分
∠BAC,∠C=2∠B,试判断
AB,AC,CD三者之间的数量关
系,并说明理由.(想一想,你会B
D
几种方法)
解:AB=AC+CD.理由如下:
方法1:在AB上截取AE=AC,
连接DE,
A
易证△AED≌△ACD(SAS),
E
.ED=CD,AE=AC,
∠AED=∠C.
B
D
.·∠AED=∠B+∠EDB,
人C=∠AED=∠B+人EDB.
又.·∠C=2∠B,
.∠B=∠EDB.
BE=DE.
.AB=AE+BE=AC DE=AC+CD
方法2:延长AC到点F,使
CF=CD,连接DF.
CF=CD.
.∠CDF=∠F
B
D
∠ACB=∠CDF+∠F,
.∴.∠ACB=2∠F.
又.·∠ACB=2∠B,
..∠B=∠F
①方法三:倍长中线法
3.如图,AD是△ABC的中线,BE交AC于点E,交AD
于点F,且AE=EF.求证:AC=BF
证明:延长AD至点G,使DG=AD,连接BG,
在△BDG和△CDA中,
BD =CD
∠BDG=∠CDA,
LDG=DA、
△BDG≌△CDA(SAS),.BG
=AC,∠CAD=∠G,
又.·AE=EF,.∴.∠AD=∠AFE,
又.·BFG=∠AFE,.∠CAD
∠BFG,
∠G=∠BFG,∴.BG=BF,.AC
BF.
A
F
E
B
D
C
G
①方法四:构造法
4.已知:如图,△ABC中,AB=AC,∠BAC=90°,点D是
AC的中点,AF⊥BD交BC于点F,连接DF.求证:
∠ADB=∠CDF.
证明:作CG∥AB交AF的延
长线于点G,
则∠ABC=∠GCB,
E
人ACG=人BAC=90°,
B
.·AF⊥BD,
∴.∠CAG+∠ADB=∠ADB+
G
∠ABD=90°,
∴.∠CAG=∠ABD,
又AC=AB,∠BAD=∠ACG=90°,
·.△ABD≌△CAG(ASA),
∠ADB=∠G,AD=CG,
.点D为AC的中点,
..CD=AD=CG,
在△DFC与△GFC中,
DC=GC.
∠ACB=∠GCF=45°,
CF=CF.
人
①方法一:翻折法
1.如图,点C,E分别为△ABD的边BD,AB上两点,且
AE=AD,CE=CD,∠D=70°,∠ECD=150°,求∠B
的度数.
解:连接AC,
.AE=AD,CE=CD,AC=AC,
△ACE≌△ACD,
E
..∠AEC=∠D=70°,
B
/BCE=180°-∠ECD=30°,
∠B=∠AEC-∠BCE=40°.
①方法二:截长补短法
2.如图,在△ABC中,AD平分
∠BAC,∠C=2∠B,试判断
AB,AC,CD三者之间的数量关
系,并说明理由.(想一想,你会B
D
几种方法)
解:AB=AC+CD.理由如下:
方法1:在AB上截取AE=AC,
连接DE,
A
易证△AED≌△ACD(SAS),
E
.ED=CD,AE=AC,
∠AED=∠C.
B
D
.·∠AED=∠B+∠EDB,
人C=∠AED=∠B+人EDB.
又.·∠C=2∠B,
.∠B=∠EDB.
BE=DE.
.AB=AE+BE=AC DE=AC+CD
方法2:延长AC到点F,使
CF=CD,连接DF.
CF=CD.
.∠CDF=∠F
B
D
∠ACB=∠CDF+∠F,
.∴.∠ACB=2∠F.
又.·∠ACB=2∠B,
..∠B=∠F
①方法三:倍长中线法
3.如图,AD是△ABC的中线,BE交AC于点E,交AD
于点F,且AE=EF.求证:AC=BF
证明:延长AD至点G,使DG=AD,连接BG,
在△BDG和△CDA中,
BD =CD
∠BDG=∠CDA,
LDG=DA、
△BDG≌△CDA(SAS),.BG
=AC,∠CAD=∠G,
又.·AE=EF,.∴.∠AD=∠AFE,
又.·BFG=∠AFE,.∠CAD
∠BFG,
∠G=∠BFG,∴.BG=BF,.AC
BF.
A
F
E
B
D
C
G
①方法四:构造法
4.已知:如图,△ABC中,AB=AC,∠BAC=90°,点D是
AC的中点,AF⊥BD交BC于点F,连接DF.求证:
∠ADB=∠CDF.
证明:作CG∥AB交AF的延
长线于点G,
则∠ABC=∠GCB,
E
人ACG=人BAC=90°,
B
.·AF⊥BD,
∴.∠CAG+∠ADB=∠ADB+
G
∠ABD=90°,
∴.∠CAG=∠ABD,
又AC=AB,∠BAD=∠ACG=90°,
·.△ABD≌△CAG(ASA),
∠ADB=∠G,AD=CG,
.点D为AC的中点,
..CD=AD=CG,
在△DFC与△GFC中,
DC=GC.
∠ACB=∠GCF=45°,
CF=CF.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
