3.3 圆与圆的位置关系课件

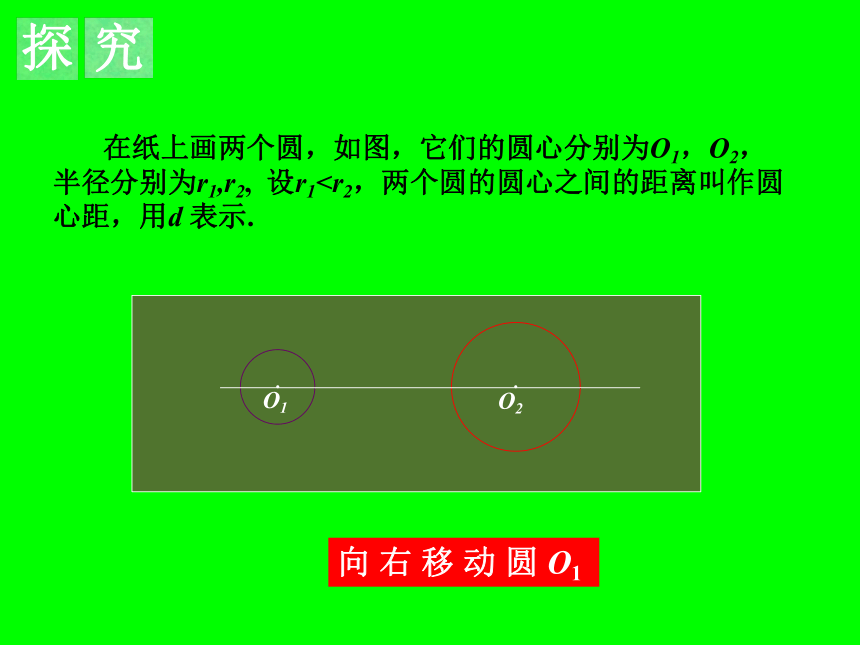
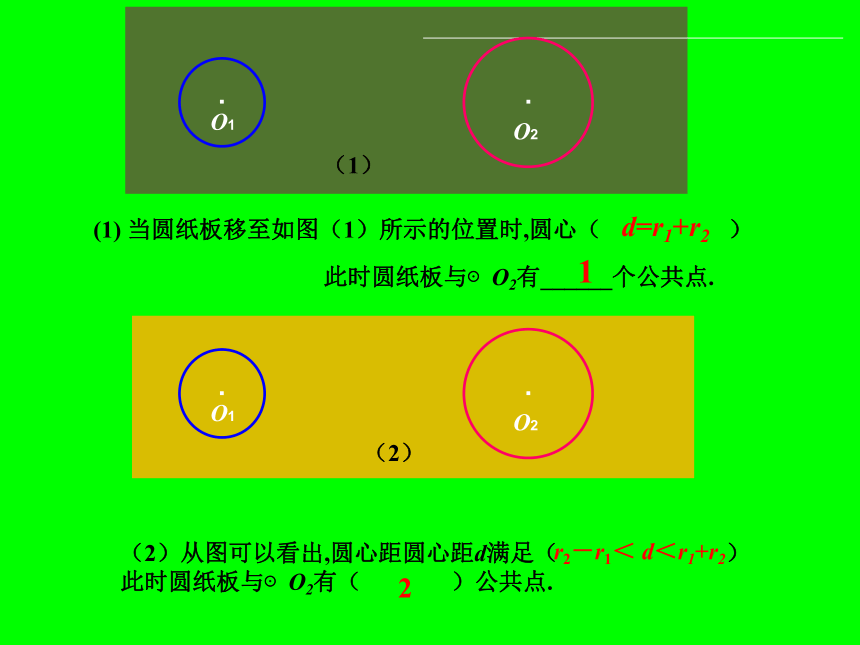
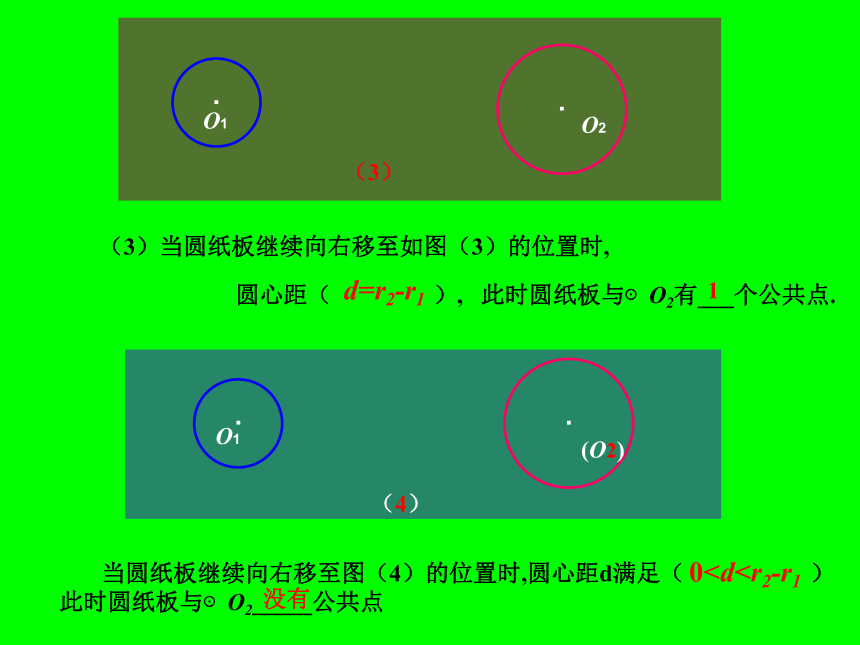
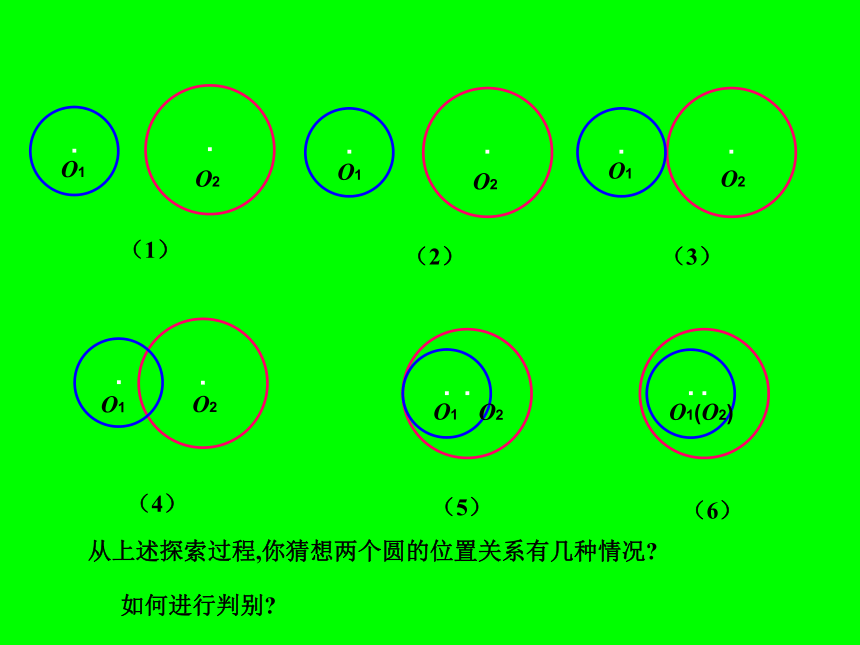
课件18张PPT。3.3 圆与圆的位置关系3.3圆与圆的位置关系 自行车两个轮胎的轮廓圆的位置关系如何？“奥运五环旗”中每两个圆的位置关系如何？举出日常生活中两个圆的位置关系的例子． 在纸上画两个圆，如图，它们的圆心分别为O1，O2，半径分别为r1,r2, 设r1此时圆纸板与⊙O2有（ ）公共点.(1) 当圆纸板移至如图（1）所示的位置时,圆心（ ）此时圆纸板与⊙O2有______个公共点.1（1）（2）2d=r1+r2r2－r1＜ d＜r1+r2圆心距（ ）, 此时圆纸板与⊙O2有___个公共点.（3）当圆纸板继续向右移至如图（3）的位置时,1· O2（3） 当圆纸板继续向右移至图（4）的位置时,圆心距d满足（ ）
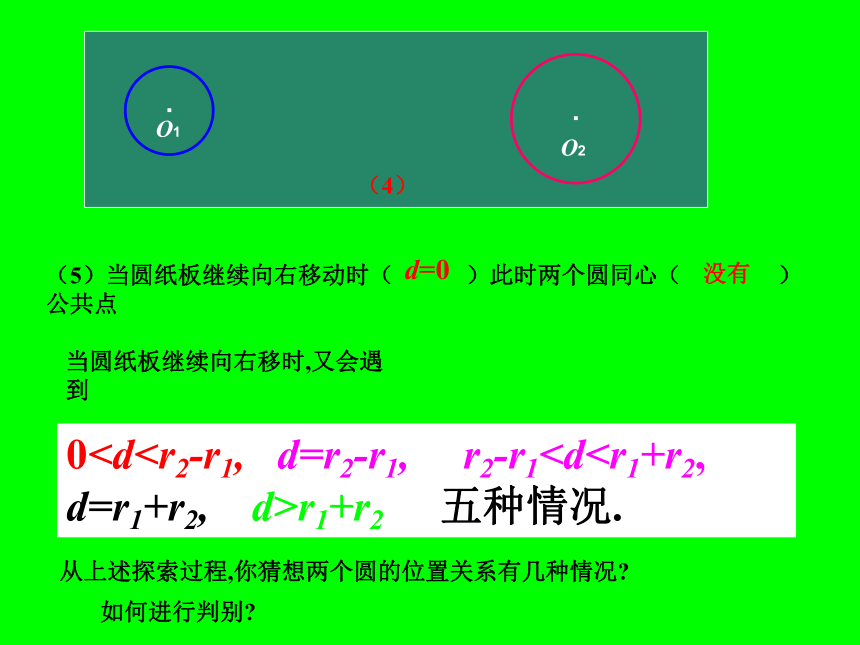
此时圆纸板与⊙O2_____公共点没有·（4）(O2)d=r2-r10r1+r2 五种情况.当圆纸板继续向右移时,又会遇到·O2·O2· O2··O1(O2)（1）（2）（3）（4）（5）（6）从上述探索过程,你猜想两个圆的位置关系有几种情况?如何进行判别? 可以证明:两个圆的位置关系有且只有7种情况: 并且每个圆上的点都在另一个圆的外部,称这两个圆外离当圆心距d>r1+r2时,两个圆没有公共点, 当d=r1+r2时,两个圆有唯一的公共点,并且除了这个公共点外,每个圆上的点都在另一个圆的外部,称这两个圆外切,如图,这个公共点叫作切点. 当r2-r1称这两个圆相交． 当d=r2-r1(设r1一个圆上的点都在另一个圆的内部,称这两个圆内切,如图,这个公共点叫作切点.当0并且一个圆上的点都在另一个圆的内部,两个圆的圆心重合,
称这两个圆内含且同心,简称它们为同心圆,
当 d=0 且 r1=r2时, 两个圆重合.·O2·O2· O2··O1(O2)如果两个圆没有公共点,那么就说这两个圆相离，如图（1）（5）（6）（4）叫做内切．如果两个圆有两个公共点，那么就说这两个圆相交，如图（3）所示 （1）（2）（3）（4）（5）（6）（6）中两圆同心是两圆内含的一种特殊其中（1）叫做外离，（5）（6）叫做内含 如果两个圆有一个公共点，那么就说这两个圆相切，如图（2）（4）其中（2）叫做外切如果两个圆没有公共点,那么就说这两个圆相离，如图（1）（5）（6）（4）叫做内切．如果两个圆有两个公共点，那么就说这两个圆相交，如图（3）所示 （6）中两圆同心是两圆内含的一种特殊其中（1）叫做外离，（5）（6）叫做内含 如果两个圆有一个公共点，那么就说这两个圆相切，如图（2）（4）其中（2）叫做外切已知圆O1和圆O2的半径分别为3cm,7cm,圆心距d=5cm,解 由于7--3=4,7+3=10,d=5, 因此4的位置关系: 练 习⑴ d=18cm; ⑵ d=17cm;⑶ d=10cm;⑷ d=5cm;d=18>r1+r2=6+17㎝∴⊙O1与⊙O2外离d=17㎝=r1+r2=17㎝∴⊙O1与⊙O2外切d= 10㎝ 求圆O2的半径.设O1的半径为r1圆O2的半径为r2，圆心距为d因为 O1 与 O2 外切所以 d = r1 + r2r2 = d－r1r2 = 15－4 = 11