黑龙江省双鸭山市重点中学2023-2024学年高二上学期开学考试数学试题(含答案)
文档属性
| 名称 | 黑龙江省双鸭山市重点中学2023-2024学年高二上学期开学考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 814.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 23:12:19 | ||
图片预览




文档简介
2022级高二学年上学期开学考试试题
数 学
(考试时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 如图为一平面图形的直观图,则此平面图形可能是选项中的( )
A. B. C. D.
2. 在中,若,,,则( )
A B. C. D.
3. 从装有两个红球和三个黑球的口袋里任取两个球,那么互斥而不对立的两个事件是( )
A. “恰好有一个黑球”与“恰好有两个黑球” B. “至少有一个黑球”与“都是红球”
C. “至少有一个黑球”与“至少有一个红球” D. “至少有一个黑球”与“都是黑球”
4. “治国之道,富民为始.”共同富裕是社会主义的本质要求,是中国式现代化的重要特征,是人民群众的共同期盼.共同富裕是全体人民通过辛勤劳动和相互帮助最终达到丰衣足食的生活水平,是消除两极分化和贫穷基础上的普遍富裕.请你运用数学学习中所学的统计知识加以分析,下列关于个人收入的统计量中,最能体现共同富裕要求的是( )
A. 平均数大,方差大 B. 平均数大,方差小
C. 平均数小,方差大 D. 平均数小,方差小
5. 已知事件A与B互斥,且,,则( )
A. B. C. D.
6. 一个正方体纸盒展开后如图所示,在关于原正方体纸盒的下列结论中正确的是( )
A. B. C. D.
7. 一组数据4.3,6.5,7.8,6.2,9.6,15.9,7.6,8.1,10,12.3,11,3,则它们的75%分位数是( )
A. 10.3 B. 10.4 C. 10.5 D. 10.6
8. 如图,生活中有很多球缺状的建筑.球被平面截下的部分叫做球缺,截面叫做球缺的底面,球缺的曲面部分叫做球冠,垂直于截面的直径被截后的线段叫做球缺的高.球冠面积公式为,球缺的体积公式为,其中R为球的半径,H为球缺的高.现有一个球被一平面所截形成两个球缺,若两个球冠的面积之比为,则这两个球缺的体积之比为( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知是虚数单位,z是复数,则下列叙述正确的是( )
A.
B. 若复数,则z为纯虚数的充要条件是
C. 若,则在复平面内z对应的点Z的集合确定的图形面积为
D. 是关于x的方程的一个根
10. 下列结论正确的是( )
A. 已知向量,,且与的夹角为锐角,则
B. 中,,,,则有两解
C. 向量,能作为所在平面内的一组基底
D. 已知平面内任意四点O,A,B,P满足,则A,B,P三点共线
11. 在中,内角A,B,C所对的边分别为a,b,c,则下列说法正确的是( )
A. 是的充要条件
B. 在中,若,,,则
C. 若,,则面积的最大值为
D. 若,则为钝角三角形
12. 如图,已知正方体的棱长为1,O为底面ABCD的中心,交平面于点E,点F为棱CD的中点,则( )
A. ,E,O三点共线 B. 异面直线BD与所成的角为
C. 点到平面的距离为 D. 过点,B,F的平面截该正方体所得截面的面积为
三、填空题:本题共4小题,每小题5分,共20分.
13. 若一个圆锥的轴截面是面积为的等边三角形,则该圆锥的侧面积为______.
14. 已知向量,满足,,,则______.
15. 数据,,的方差为,则数据,,的平均数为______.
16. 棱长为6的正方体内有一个棱长为x的正四面体,正四面体的中心(正四面体的中心就是该四面体外接球的球心)与正方体的中心重合,且该四面体可以在正方体内任意转动,则x的最大值为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
(1)已知,且,,求.
(2)已知向量,,求与的夹角值.
18.(本小题满分12分)
甲、乙、丙三人组成一组,参加一个闯关游戏团体赛.三人各自独立闯关,其中甲闯关成功的概率为,甲、乙都闯关成功的频率为,乙、丙都闯关成功的概率为,每人闯关成功记2分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;
(2)求团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加复赛,求该小组参加复赛的概率.
19.(本小题满分12分)
如图,四棱锥中,ABCD为正方形,E为PC的中点,平面平面ABCD,.
(1)证明:平面BDE;
(2)求三棱锥的体积.
20.(本小题满分12分)
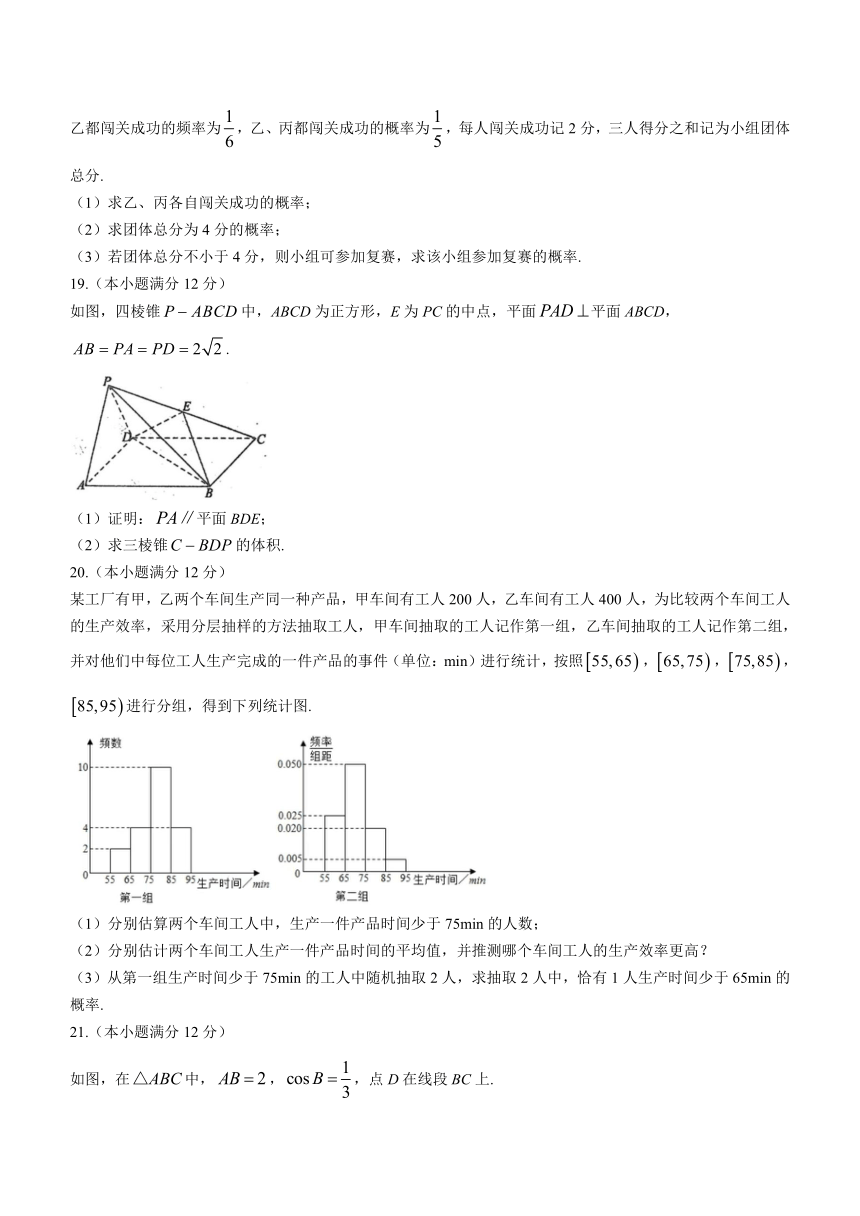
某工厂有甲,乙两个车间生产同一种产品,甲车间有工人200人,乙车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:min)进行统计,按照,,,进行分组,得到下列统计图.
(1)分别估算两个车间工人中,生产一件产品时间少于75min的人数;
(2)分别估计两个车间工人生产一件产品时间的平均值,并推测哪个车间工人的生产效率更高?
(3)从第一组生产时间少于75min的工人中随机抽取2人,求抽取2人中,恰有1人生产时间少于65min的概率.
21.(本小题满分12分)
如图,在中,,,点D在线段BC上.
(1)若,求AD的长;
(2)若,的面积为,求的值.
22.(本小题满分12分)
如图,四边形与四边形是全等的矩形,.
(1)若P是棱的中点,求证:平面平面;
(2)若P是棱上的点,直线BP与平面所成角的正切值为,求二面角的正弦值.
高二(上)数学开学考试答案
1 2 3 4 5 6 7 8 9 10 11 12
C D A B B A C D AD CD ACD ABD
13. 14. 1 15. 7或-5 16.
四、解答题: 本大题共 6小题, 其中第17题10分,其余小题每题 12分,共70分.
17. 解:(1)20或-20
(2)
18. 解:(1)三人各自独立闯关,其中甲闯关成功的概率为,
甲、乙都闯关成功的概率为,乙、丙都闯关成功的概率为,
设乙闯关成功的概率为,丙闯关成功的概率为,
∵乙丙独立闯关,
根据独立事件同时发生的概率公式得:.
解得,.
即乙闯关成功的概率为,丙闯关成功的概率为.
(2)团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一人没过关.
设“团体总分为4分”为事件A,
则,
即团体总分为4分的概率为.
(3)团体总分不小于4分,即团体总分为4分或6分,设“团体总分不小于4分”为事件B,
由(2)知团体总分为4分的概率为,
团体总分为6分,即3人都闯关成功的概率为.
所以参加复赛的概率为.
即该小组参加复赛的概率为.
19.(1)证明:连接AC交BD于点O,连接OE,
因为四边形ABCD为正方形,所以点O为AC的中点,
又E为PC的中点,所以,
又因为平面BDE,平面BDE,所以平面BDE.
(2)解:∵四边形ABCD为正方形,则,
因为,
所以.
20.(本小题满分 12分)
(Ⅰ)第一组工人20人,其中在75min内(不含75min)生产完成一件产品的有6人,
∴甲车间工人中生产一件产品时间少于75min的人数为(人),
第二组工人40人.其中在75min内(不含75min)生产完成一件产品的有
人,
∴乙车间工人中生产一件产品时间少于75min的人数为(人).
(Ⅱ)第一组平均时间为:,
第二组平均时间为:,
∵,∴乙车间工人生产效率更高.
(Ⅲ)由题意得,第一组生产时间少于75min的工人有6人,
其中生产时间少于65min的有2人,分别用,代表,
生产时间不少于65min的工人用,,,代表,
抽取2人基本事件空间为:
,共15个基本事件.
设事件A:恰有1人生产时间少于65min,
则.
21.(本小题满分 12分)
(1)∵中,,
∴,
∵,∴,
在中,由正弦定理得,
∴,
综上所述,结论是:AD的长为.
(2)设,则,∴,
∴,的面积为,
∴,
∴,,
中,由余弦定理得
,
在中,由正弦定理,
即,∴,
中,由正弦定理得,
即,
∴,
∵,
∴,
综上所述,结论是:.
22. 证明:(1)由题意知 ,所以,
又因为,且,平面,平面,
所以平面,
又平面,所以. ……2分
,即,所以,所以,
同理,所以,即. ……4分
又由于,所以,且,
又平面,平面,
所以平面,
又因为面,所以平面平面. ……5分
解:(2)由(1)知,平面,所以CP是直线BP在平面内的射影,
所以就是直线BP与平面所成的角,即,
所以,所以由勾股定理得, ……7分
又由(1)知,,,两两垂直,以,,所在直线分别为x,y,z轴建立空间直角坐标系.
设,则,,,
,,
设平面的一个法向量为,
由于,所以,即,
令,则,,即, ……9分
易知平面的一个法向量为, ……10分
设二面角的大小为,可知为锐角,所以. …11分
故二面角的正弦值为. ……12分
数 学
(考试时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 如图为一平面图形的直观图,则此平面图形可能是选项中的( )
A. B. C. D.
2. 在中,若,,,则( )
A B. C. D.
3. 从装有两个红球和三个黑球的口袋里任取两个球,那么互斥而不对立的两个事件是( )
A. “恰好有一个黑球”与“恰好有两个黑球” B. “至少有一个黑球”与“都是红球”
C. “至少有一个黑球”与“至少有一个红球” D. “至少有一个黑球”与“都是黑球”
4. “治国之道,富民为始.”共同富裕是社会主义的本质要求,是中国式现代化的重要特征,是人民群众的共同期盼.共同富裕是全体人民通过辛勤劳动和相互帮助最终达到丰衣足食的生活水平,是消除两极分化和贫穷基础上的普遍富裕.请你运用数学学习中所学的统计知识加以分析,下列关于个人收入的统计量中,最能体现共同富裕要求的是( )
A. 平均数大,方差大 B. 平均数大,方差小
C. 平均数小,方差大 D. 平均数小,方差小
5. 已知事件A与B互斥,且,,则( )
A. B. C. D.
6. 一个正方体纸盒展开后如图所示,在关于原正方体纸盒的下列结论中正确的是( )
A. B. C. D.
7. 一组数据4.3,6.5,7.8,6.2,9.6,15.9,7.6,8.1,10,12.3,11,3,则它们的75%分位数是( )
A. 10.3 B. 10.4 C. 10.5 D. 10.6
8. 如图,生活中有很多球缺状的建筑.球被平面截下的部分叫做球缺,截面叫做球缺的底面,球缺的曲面部分叫做球冠,垂直于截面的直径被截后的线段叫做球缺的高.球冠面积公式为,球缺的体积公式为,其中R为球的半径,H为球缺的高.现有一个球被一平面所截形成两个球缺,若两个球冠的面积之比为,则这两个球缺的体积之比为( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知是虚数单位,z是复数,则下列叙述正确的是( )
A.
B. 若复数,则z为纯虚数的充要条件是
C. 若,则在复平面内z对应的点Z的集合确定的图形面积为
D. 是关于x的方程的一个根
10. 下列结论正确的是( )
A. 已知向量,,且与的夹角为锐角,则
B. 中,,,,则有两解
C. 向量,能作为所在平面内的一组基底
D. 已知平面内任意四点O,A,B,P满足,则A,B,P三点共线
11. 在中,内角A,B,C所对的边分别为a,b,c,则下列说法正确的是( )
A. 是的充要条件
B. 在中,若,,,则
C. 若,,则面积的最大值为
D. 若,则为钝角三角形
12. 如图,已知正方体的棱长为1,O为底面ABCD的中心,交平面于点E,点F为棱CD的中点,则( )
A. ,E,O三点共线 B. 异面直线BD与所成的角为
C. 点到平面的距离为 D. 过点,B,F的平面截该正方体所得截面的面积为
三、填空题:本题共4小题,每小题5分,共20分.
13. 若一个圆锥的轴截面是面积为的等边三角形,则该圆锥的侧面积为______.
14. 已知向量,满足,,,则______.
15. 数据,,的方差为,则数据,,的平均数为______.
16. 棱长为6的正方体内有一个棱长为x的正四面体,正四面体的中心(正四面体的中心就是该四面体外接球的球心)与正方体的中心重合,且该四面体可以在正方体内任意转动,则x的最大值为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
(1)已知,且,,求.
(2)已知向量,,求与的夹角值.
18.(本小题满分12分)
甲、乙、丙三人组成一组,参加一个闯关游戏团体赛.三人各自独立闯关,其中甲闯关成功的概率为,甲、乙都闯关成功的频率为,乙、丙都闯关成功的概率为,每人闯关成功记2分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;
(2)求团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加复赛,求该小组参加复赛的概率.
19.(本小题满分12分)
如图,四棱锥中,ABCD为正方形,E为PC的中点,平面平面ABCD,.
(1)证明:平面BDE;
(2)求三棱锥的体积.
20.(本小题满分12分)
某工厂有甲,乙两个车间生产同一种产品,甲车间有工人200人,乙车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:min)进行统计,按照,,,进行分组,得到下列统计图.
(1)分别估算两个车间工人中,生产一件产品时间少于75min的人数;
(2)分别估计两个车间工人生产一件产品时间的平均值,并推测哪个车间工人的生产效率更高?
(3)从第一组生产时间少于75min的工人中随机抽取2人,求抽取2人中,恰有1人生产时间少于65min的概率.
21.(本小题满分12分)
如图,在中,,,点D在线段BC上.
(1)若,求AD的长;
(2)若,的面积为,求的值.
22.(本小题满分12分)
如图,四边形与四边形是全等的矩形,.
(1)若P是棱的中点,求证:平面平面;
(2)若P是棱上的点,直线BP与平面所成角的正切值为,求二面角的正弦值.
高二(上)数学开学考试答案
1 2 3 4 5 6 7 8 9 10 11 12
C D A B B A C D AD CD ACD ABD
13. 14. 1 15. 7或-5 16.
四、解答题: 本大题共 6小题, 其中第17题10分,其余小题每题 12分,共70分.
17. 解:(1)20或-20
(2)
18. 解:(1)三人各自独立闯关,其中甲闯关成功的概率为,
甲、乙都闯关成功的概率为,乙、丙都闯关成功的概率为,
设乙闯关成功的概率为,丙闯关成功的概率为,
∵乙丙独立闯关,
根据独立事件同时发生的概率公式得:.
解得,.
即乙闯关成功的概率为,丙闯关成功的概率为.
(2)团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一人没过关.
设“团体总分为4分”为事件A,
则,
即团体总分为4分的概率为.
(3)团体总分不小于4分,即团体总分为4分或6分,设“团体总分不小于4分”为事件B,
由(2)知团体总分为4分的概率为,
团体总分为6分,即3人都闯关成功的概率为.
所以参加复赛的概率为.
即该小组参加复赛的概率为.
19.(1)证明:连接AC交BD于点O,连接OE,
因为四边形ABCD为正方形,所以点O为AC的中点,
又E为PC的中点,所以,
又因为平面BDE,平面BDE,所以平面BDE.
(2)解:∵四边形ABCD为正方形,则,
因为,
所以.
20.(本小题满分 12分)
(Ⅰ)第一组工人20人,其中在75min内(不含75min)生产完成一件产品的有6人,
∴甲车间工人中生产一件产品时间少于75min的人数为(人),
第二组工人40人.其中在75min内(不含75min)生产完成一件产品的有
人,
∴乙车间工人中生产一件产品时间少于75min的人数为(人).
(Ⅱ)第一组平均时间为:,
第二组平均时间为:,
∵,∴乙车间工人生产效率更高.
(Ⅲ)由题意得,第一组生产时间少于75min的工人有6人,
其中生产时间少于65min的有2人,分别用,代表,
生产时间不少于65min的工人用,,,代表,
抽取2人基本事件空间为:
,共15个基本事件.
设事件A:恰有1人生产时间少于65min,
则.
21.(本小题满分 12分)
(1)∵中,,
∴,
∵,∴,
在中,由正弦定理得,
∴,
综上所述,结论是:AD的长为.
(2)设,则,∴,
∴,的面积为,
∴,
∴,,
中,由余弦定理得
,
在中,由正弦定理,
即,∴,
中,由正弦定理得,
即,
∴,
∵,
∴,
综上所述,结论是:.
22. 证明:(1)由题意知 ,所以,
又因为,且,平面,平面,
所以平面,
又平面,所以. ……2分
,即,所以,所以,
同理,所以,即. ……4分
又由于,所以,且,
又平面,平面,
所以平面,
又因为面,所以平面平面. ……5分
解:(2)由(1)知,平面,所以CP是直线BP在平面内的射影,
所以就是直线BP与平面所成的角,即,
所以,所以由勾股定理得, ……7分
又由(1)知,,,两两垂直,以,,所在直线分别为x,y,z轴建立空间直角坐标系.
设,则,,,
,,
设平面的一个法向量为,
由于,所以,即,
令,则,,即, ……9分
易知平面的一个法向量为, ……10分
设二面角的大小为,可知为锐角,所以. …11分
故二面角的正弦值为. ……12分
同课章节目录
