第四章:图形的认识导学案
图片预览



文档简介
第一课时《几何图形》
任教者:高新球 王文昭 黄喜华 王安元
学习目标:知道几何图形、立体图形、平面图形的意义,学会从不同方向看立体图形得到不同形状的平面图形,认识基本的立体图形及其展开图并会相互转化。
课 前 预 习 单
1、看课本P114多姿多彩的图形世界,各种各样的物体除了具有颜色、质量、材质等性质外,还具有 (如方的、圆的), (如长度、面积、体积等)和 (如相交、垂直、平行等),物体的 、 和 是几何中研究的内容。
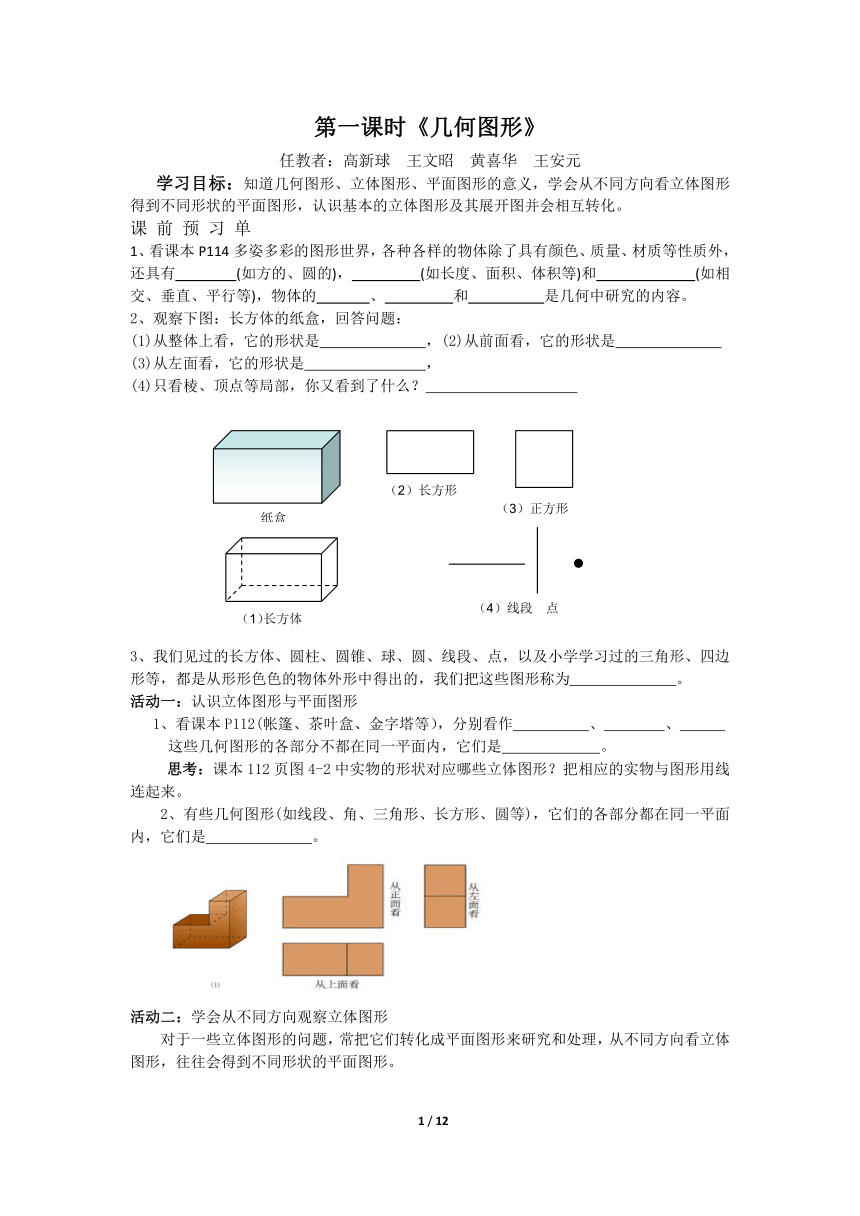
2、观察下图:长方体的纸盒,回答问题:
(1)从整体上看,它的形状是 ,(2)从前面看,它的形状是
(3)从左面看,它的形状是 ,
(4)只看棱、顶点等局部,你又看到了什么?
3、我们见过的长方体、圆柱、圆锥、球、圆、线段、点,以及小学学习过的三角形、四边形等,都是从形形色色的物体外形中得出的,我们把这些图形称为 。
活动一:认识立体图形与平面图形
1、看课本P112(帐篷、茶叶盒、金字塔等),分别看作 、 、
这些几何图形的各部分不都在同一平面内,它们是 。
思考:课本112页图4-2中实物的形状对应哪些立体图形?把相应的实物与图形用线连起来。
2、有些几何图形(如线段、角、三角形、长方形、圆等),它们的各部分都在同一平面内,它们是 。
活动二:学会从不同方向观察立体图形
对于一些立体图形的问题,常把它们转化成平面图形来研究和处理,从不同方向看立体图形,往往会得到不同形状的平面图形。
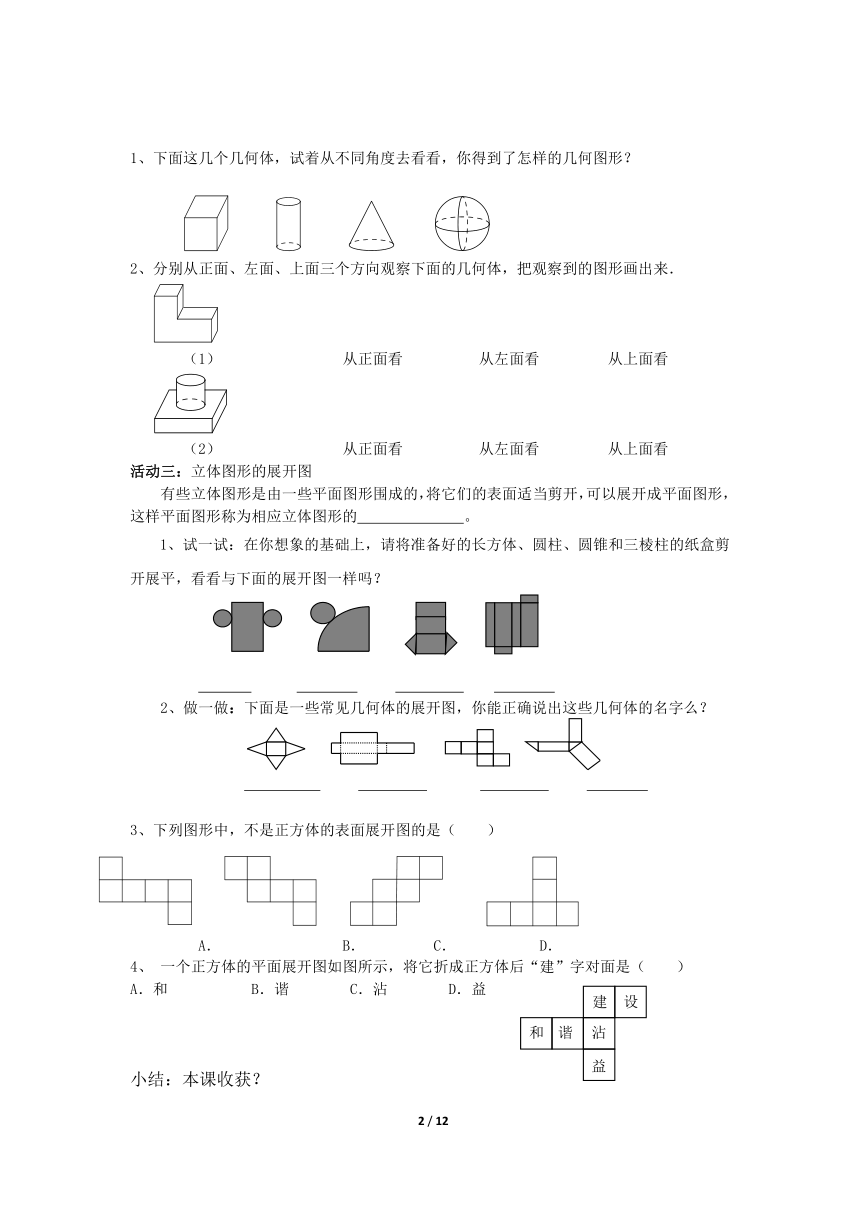
1、下面这几个几何体,试着从不同角度去看看,你得到了怎样的几何图形?
HYPERLINK "http://http://www.xkb1.com" HYPERLINK "http://http://www.xkb1.com" HYPERLINK "http://http://www.xkb1.com" HYPERLINK "http://http://www.xkb1.com"
2、分别从正面、左面、上面三个方向观察下面的几何体,把观察到的图形画出来.
HYPERLINK "http://http://www.xkb1.com"
(1) 从正面看 从左面看 从上面看
HYPERLINK "http://http://www.xkb1.com"
(2) 从正面看 从左面看 从上面看
活动三:立体图形的展开图
有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形,这样平面图形称为相应立体图形的 。
1、试一试:在你想象的基础上,请将准备好的长方体、圆柱、圆锥和三棱柱的纸盒剪开展平,看看与下面的展开图一样吗?
2、做一做:下面是一些常见几何体的展开图,你能正确说出这些几何体的名字么?
3、下列图形中,不是正方体的表面展开图的是( )
A. B. C. D.
4、 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )
A.和 B.谐 C.沾 D.益
小结:本课收获?
第2课时 直线、射线、线段(1)
任教者:高新球 王文昭 黄喜华 王安元
学习目标:
1、认识直线、射线和线段。
2、能正确区分直线、射线和线段;掌握它们的联系和区别。
3、掌握点与直线的两种位置关系及直线的基本性质。
一、自主预习
1.在小学已经学过了直线、射线、线段.请你画出一条直线、一条射线、一条线段?
直线 射线 线段
2.填写下列表格:
端点个数 延伸方向 能否度量
线段
射线
直线
二、合作探究
1、直线的性质
(1)如果你想将一根细木条固定在墙上,至少需要几个钉子?操作一下,试试看。
答:
(2)经过一个已知点的直线,可以画多少条直线?请画图说明。
答: O ·
(3)经过两个已知点画直线,可以画多少条直线?请画图试试。
· ·
答: A B
猜想:如果将细木条抽象成直线,将钉子抽象为点,你可以得到什么结论?
直线的基本性质:
经过两点有 条直线,并且 条直线;
简述为:
举例说明直线的性质在日常生活中的应用:
(1) 在挂窗帘时,只要在两边钉两颗钉子扯上线即可,这是因为
(2)建筑工人在砌墙时拉参照线,木工师傅锯木板时,用墨盒弹墨线,都是根据
(3)你还能从生活中举出应用直线的基本性质的例子吗?试试看:
2、直线有两种表示方法:①用一个小写字母表示;②用两个大写字母表示。
平面上一个点与一条直线的位置有什么关系?
①点在直线上;②点在直线外。
当两条直线有一个共公点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
3、射线和线段的表示方法:
如图。显然,射线和线段都是直线的一部分。
图①中的线段记作线段AB或线段a;图②中的射线记作射线OA或射线m。
注意:用两个大写字母表示射线时,表示端点的字母一定要写在前面。
思考:直线、射线和线段有什么联系和区别?
三.巩固提高
1.下列给线段取名正确的是 ( )
A.线段M B.线段m C.线段Mm D.线段mn
2.如图,若射线AB上有一点C,下列与射线AB是同一条射线的是 ( )
A.射线BA B.射线AC
C.射线BC D.射线CB
3.下列语句中正确的个数有 ( )
①直线MN与直线NM是同一条直线 ②射线AB与射线BA是同一条射线
③线段PQ与线段QP是同一条线段
④直线上一点把这条直线分成的两部分都是射线.
A.1个 B.2个 C.3个 D.4个
4.课本119页练习
四.反思升华
1.如图,线段AB上有两点C、D,则共有 条线段。
2.变形题:往返于甲、乙两地的客车中途要停靠三个车站,有多少种不同的票价?要准备多少种不同的车票?
第3课时 直线、射线、线段(2)
任教者:高新球 王文昭 黄喜华 王安元
学习目的:
学会作一条线段等于已知线段
会比较两条线段的长短。
识记线段的中点、会用线段的中点进行简单的计算
一、自主预习
1、过A、B、C三点作直线,小明说有三条,小颖说有一条,小林说不是一条就是三条,你认为 的说法是对的。
二、合作探究
问题:现有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根木棒的长?
上面的实际问题可以转化为下面的数学问题:已知线段a,画一条线段等于已知线段。
1.作一条线段等于已知线段
现在我们来解决这个问题。
作法:
(1)作射线AM
(2)在AM上截取AB= a。
则线段AB为所求。
应用:已知线段a、b,求作线段AB=a+b。
解:(1)作射线AM;
(2)在AM上顺次截取AC=a,CB= b。
则AB= a+b为所求。
做一做:作线段AB=a-b。
2、比较两条线段的长短
两条线段可能相等,也可能不相等,那么怎样比较两条线段的长短呢?
我们先来回答下面的问题。
怎样比较两个同学的身高?
一是用尺子测量;二是站在一起比(脚在同一高度)。
如果把两个同学看成两条线段,那么比较两条线段就有两种方法。
(1)度量法:用刻度尺分别量出两条线段的长度从而进行比较。
( 2)把一条线段移到另一条线段上,使一端对齐,从而进行比较,我们称为叠合法。(如图)
AB<CD AB>CD AB=CD
3、线段的中点及等分点
如图(1),点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点;
记作AM=MB或AM=MB=1/2AB或2AM=2MB=AB。
如图(2),点M、N把线段AB分成相等的三段AM、MN、NB,点M、N叫做线段AB的三等分点。类似地,还有四等分点,等等。4、线段的性质
请同学们思考课本131页的思考?
结论:
两点所连的线中,
简单地说成:___________________________________
你能举出这条性质在生活中的一些应用吗?
两点间的距离的定义:___________________________________
注意:距离是用“数”来度量的,它是线段的长度,而不是线段本身。
三、巩固提高
1、课本131页练习1、2
2、在直线上顺次取A、B、C三点,使 AB=4㎝,BC=3㎝,点O是线段AC的中点,则线段OB的长是〔 〕
A、2㎝ B、1.5㎝ C、0.5㎝ D、3.5㎝
3、已知线段AB=5㎝,C是直线AB上一点,若BC=2㎝,则线段AC的长为
四.、反思升华
1、把弯曲的河道改直后,缩短了河道的长度,这是因为 ;
2、已知,如图,AB=16㎝,C是BC的中点,且AC=10㎝,D是AC的中点,E是BC的中点,求线段DE的长。
第4课时 角与角的大小比较
任教者:高新球 王文昭 黄喜华 王安元
[学习目标]:
1.理解角、平角、周角的定义
2.能正确地表示角、会比较角的大小
3.认识角的平分线
重点:角的表示方法与大小比较
难点:角的表示方法
[学法指导]
自主学习 小组合作探究
[课前预习]
1、角的定义(1): 角是由有_________________的两条射线组成的图形,
这个公共端点是角的__________,这两条射线是角的_________________。
2、角的定义(2): 一条射线绕着它的_________从一个位置_________到另一位置时所成的图形叫做角。
3、角的大小由角的始边绕顶点旋转至终边时________________决定。
4、当射线绕着端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做_______角。
5、当射线绕着端点旋转一周,又重新回到原来的位置时,所成的角叫做______角。
[合作探究]
[活动一]:角的表示方法
1、如下图中的角,你能用几种方法把它表示出来?
[活动二]:角的大小比较方法
下面的三组图形,每组中都有两个角,你能判断它们的大小吗?说说你的方法.
[拓展延伸]:请同学们将手中的角对折,你发现了什么?
角的平分线:
如图,射线OP是∠AOB的角平分线,那么图这几个角
有怎样的大小关系?
2、如图,已知OB、OC是∠AOB的三等分线,试说出几个你能得到的正确结论:
第5课时 角的度量
任教者:高新球 王文昭 黄喜华 王安元
教学目的
1.理解1度的角的概念及角的分类。
2、理解余角及补角的概念及性质。
3、掌握角的大小的计算。
一、 自学自测
1、1度的角怎样定义: 。
2、角的换算单位:1°= ′= ″ 1″= ′= °
3、角的.分类
二、余角及补角的定义和性质:
1、互为余角和互为补角的概念
两角之和等于 度,这样的两个角叫做互为余角。
两角之和等于 度,这样的两个角叫做互为补角。
1)若∠1 + ∠2 =180 °, 则
2)若∠1和∠2互补,则 .
3)若∠3 + ∠4 =90 °,则 .
4)若∠3和∠4互余,则 .
2、互为余角及互为补角的性质
同角或等角的余角 ;同角或等角的补角 。
应用举例:∵∠1=∠2, ∠1+∠3=90°,∠ 2+∠4=90°(已知)
∴∠3=∠4(等角的余角相等)
填理由:∵∠1+∠2=180°,∠ 1+∠3=180°( )
∴∠3=∠4( )
3.如图,已知∠AOB与∠BOD互为余角,OC是∠BOD的角平分线,
∠AOB=29.66°,求∠COD的度数。
三、角的大小的计算:
1、70°39′的余角是 ,补角是 。
2、如果一个角的补角是150 ° ;那么这个角的余角是 。
3.根据图形填空:(1)∠DOB=∠DOC+∠
(2)∠AOD=∠DOB-∠ = -∠AOC
(3)∠DOC+∠BOA-∠DOB=
5.如图,若∠ABC=90 °,BP平分∠ ABD,
(1)若 ∠CBD=30° ,求∠ABP的度数。
(2)若∠CBD=x°,求∠ ABP的度数。
四 讨论更正 合作探究
五 小结:你学会了什么?
六 达标训练
1.∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.1)根据图形填空:
①∠DBA=∠DBC+
②∠DBC=∠DBP- =∠DBA-
③∠DBP+∠ABC-∠ABD=
2)变式:如图若∠ABC=90 ,∠CBD=30 ,你能求出哪些角的度数
第6课时 图形的认识总复习学案
任教者:高新球 王文昭 黄喜华 王安元
一、学习目标:(1)认识一些简单的几何体及其平面展开图。
(2)掌握“直线、射线、线段、角”这些基本图形的概念、性质、表示方法和画法。
(3)掌握线段中点、角平分线、互余(或互补)等概念,并会进行相关的推理和计算;
二、学习探索:
(一)平面图形与立体图形
1.下列物体:①圆筒形的易拉罐;②地球;③数学课本;④足球;⑤火柴盒;⑥文具盒中,形状类似于棱柱的有 (填写序号)
2.小亮为即将参加考试的好友小杰制作了一个正方体礼品盒(如图所示),六个面上各有一个字,连起来就是“预祝考试成功”,其中“预”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是( )
3埃及金字塔是世界奇迹之一,它充满了神秘与梦幻,请观察
如图所示的金字塔图片,试判断其形状类似于( )
A.圆柱 B.球 C.圆锥 D.棱锥
答案:(1)③⑤⑥;(2)C;(3)D;
(二)直线、射线、线段
1.下列说法:①射线MN与射线MP表示同一条射线;②平角是一条直线;③连接两点的线段长叫做这两点之间的距离;④若,则、和互为余角,其中错误的有( ) A.1个 B.2个 C.3个 D.4个
2.下列语句正确的是( ) A.画直线 B.角平分线是一条线段
C.画射线 D.延长线段AB到点C,使得
3.已知直线上有两点M、N,且,再找一点P,使,则P点的位置在( )。
A.直线上; B.直线外; C.直线上或直线外; D.不存在这一点P;
4.石匠师傅在用大理石铺地时,总是先在一侧的两头将两口根木棒插入地中,同时在中间拉上一根细线,铺地时沿着细线铺设,理由是 。
5.下列说法正确的是( )
A.直线的一半是射线; B.线段AB的长度就是A、B两间的距离;
C.直线上两点间的部分叫射线; D.若点P使,则点P是线段AB的中点;
6.如图,已知线段,点M为AB的中点,点P在MB上,点N为PB的中点,且。求PM的长。
7.在自来水主水管道AB的两旁有两个住宅小区C、D,现要在主水管道上开一个接水口P,往C、D两个小区铺设水管。为了节省铺水管的用料,
接口P应开在水管AB的什么位置?在图中画出来,
并说明依据的数学原理。
(三)角的度量与比较:
【基本知识点】
1.角的定义1:有 端点的两条 组成的图形叫角。其中公共端点叫角的 ,两条射线叫角的 .角的两条边是 线。
角的定义2:角也可以看作 而形成的图形;
2.角的度量单位之间的换算关系是: ;
3.从一个角的顶点出发,把这个角分成相等的两个角的射线,
叫做这个角的 。类似的还可以将角分成三等分、四等分。
几何语言表达: ∵如图,OC是∠AOB的平分线
∴= = ∠AOB 或 = =
4.如果两个角的和等于90°(直角),就说这两个角互为 ,通常记的余角是:
(用数学式表示);如果两个角的和等于180°(平角),就收这两个角互为 ,通常记:的补角是 (用数学式表示)。
补角性质:同角或等角的补角 ;余角性质:同角或等角的余角 。
纸盒
(1)长方体
(2)长方形
(3)正方形
(4)线段 点
建
设
和
谐
沾益
益
B BB
A
直线AB
·
·
a
直线a
O
b
a
点B在直线外
·
B BB
·
点A在直线上
A
·
a
·
B BB
A
O
A
m
·
②
①
A B C
A C D B
M
B
·
·
A
a
b
C
M
B
·
·
A
A(C)
B
(D)
A(C)
(D)
B
A(C)
B(D)
A
B
M
A
B
M
N
(1)
(2)
()
A
B
C
D
E
·
·
·
A
B
O
C
D
A
B
D
C
P
A
B
D
C
P
1 / 12
任教者:高新球 王文昭 黄喜华 王安元
学习目标:知道几何图形、立体图形、平面图形的意义,学会从不同方向看立体图形得到不同形状的平面图形,认识基本的立体图形及其展开图并会相互转化。
课 前 预 习 单
1、看课本P114多姿多彩的图形世界,各种各样的物体除了具有颜色、质量、材质等性质外,还具有 (如方的、圆的), (如长度、面积、体积等)和 (如相交、垂直、平行等),物体的 、 和 是几何中研究的内容。
2、观察下图:长方体的纸盒,回答问题:
(1)从整体上看,它的形状是 ,(2)从前面看,它的形状是
(3)从左面看,它的形状是 ,
(4)只看棱、顶点等局部,你又看到了什么?
3、我们见过的长方体、圆柱、圆锥、球、圆、线段、点,以及小学学习过的三角形、四边形等,都是从形形色色的物体外形中得出的,我们把这些图形称为 。
活动一:认识立体图形与平面图形
1、看课本P112(帐篷、茶叶盒、金字塔等),分别看作 、 、
这些几何图形的各部分不都在同一平面内,它们是 。
思考:课本112页图4-2中实物的形状对应哪些立体图形?把相应的实物与图形用线连起来。
2、有些几何图形(如线段、角、三角形、长方形、圆等),它们的各部分都在同一平面内,它们是 。
活动二:学会从不同方向观察立体图形
对于一些立体图形的问题,常把它们转化成平面图形来研究和处理,从不同方向看立体图形,往往会得到不同形状的平面图形。
1、下面这几个几何体,试着从不同角度去看看,你得到了怎样的几何图形?
HYPERLINK "http://http://www.xkb1.com" HYPERLINK "http://http://www.xkb1.com" HYPERLINK "http://http://www.xkb1.com" HYPERLINK "http://http://www.xkb1.com"
2、分别从正面、左面、上面三个方向观察下面的几何体,把观察到的图形画出来.
HYPERLINK "http://http://www.xkb1.com"
(1) 从正面看 从左面看 从上面看
HYPERLINK "http://http://www.xkb1.com"
(2) 从正面看 从左面看 从上面看
活动三:立体图形的展开图
有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形,这样平面图形称为相应立体图形的 。
1、试一试:在你想象的基础上,请将准备好的长方体、圆柱、圆锥和三棱柱的纸盒剪开展平,看看与下面的展开图一样吗?
2、做一做:下面是一些常见几何体的展开图,你能正确说出这些几何体的名字么?
3、下列图形中,不是正方体的表面展开图的是( )
A. B. C. D.
4、 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )
A.和 B.谐 C.沾 D.益
小结:本课收获?
第2课时 直线、射线、线段(1)
任教者:高新球 王文昭 黄喜华 王安元
学习目标:
1、认识直线、射线和线段。
2、能正确区分直线、射线和线段;掌握它们的联系和区别。
3、掌握点与直线的两种位置关系及直线的基本性质。
一、自主预习
1.在小学已经学过了直线、射线、线段.请你画出一条直线、一条射线、一条线段?
直线 射线 线段
2.填写下列表格:
端点个数 延伸方向 能否度量
线段
射线
直线
二、合作探究
1、直线的性质
(1)如果你想将一根细木条固定在墙上,至少需要几个钉子?操作一下,试试看。
答:
(2)经过一个已知点的直线,可以画多少条直线?请画图说明。
答: O ·
(3)经过两个已知点画直线,可以画多少条直线?请画图试试。
· ·
答: A B
猜想:如果将细木条抽象成直线,将钉子抽象为点,你可以得到什么结论?
直线的基本性质:
经过两点有 条直线,并且 条直线;
简述为:
举例说明直线的性质在日常生活中的应用:
(1) 在挂窗帘时,只要在两边钉两颗钉子扯上线即可,这是因为
(2)建筑工人在砌墙时拉参照线,木工师傅锯木板时,用墨盒弹墨线,都是根据
(3)你还能从生活中举出应用直线的基本性质的例子吗?试试看:
2、直线有两种表示方法:①用一个小写字母表示;②用两个大写字母表示。
平面上一个点与一条直线的位置有什么关系?
①点在直线上;②点在直线外。
当两条直线有一个共公点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
3、射线和线段的表示方法:
如图。显然,射线和线段都是直线的一部分。
图①中的线段记作线段AB或线段a;图②中的射线记作射线OA或射线m。
注意:用两个大写字母表示射线时,表示端点的字母一定要写在前面。
思考:直线、射线和线段有什么联系和区别?
三.巩固提高
1.下列给线段取名正确的是 ( )
A.线段M B.线段m C.线段Mm D.线段mn
2.如图,若射线AB上有一点C,下列与射线AB是同一条射线的是 ( )
A.射线BA B.射线AC
C.射线BC D.射线CB
3.下列语句中正确的个数有 ( )
①直线MN与直线NM是同一条直线 ②射线AB与射线BA是同一条射线
③线段PQ与线段QP是同一条线段
④直线上一点把这条直线分成的两部分都是射线.
A.1个 B.2个 C.3个 D.4个
4.课本119页练习
四.反思升华
1.如图,线段AB上有两点C、D,则共有 条线段。
2.变形题:往返于甲、乙两地的客车中途要停靠三个车站,有多少种不同的票价?要准备多少种不同的车票?
第3课时 直线、射线、线段(2)
任教者:高新球 王文昭 黄喜华 王安元
学习目的:
学会作一条线段等于已知线段
会比较两条线段的长短。
识记线段的中点、会用线段的中点进行简单的计算
一、自主预习
1、过A、B、C三点作直线,小明说有三条,小颖说有一条,小林说不是一条就是三条,你认为 的说法是对的。
二、合作探究
问题:现有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根木棒的长?
上面的实际问题可以转化为下面的数学问题:已知线段a,画一条线段等于已知线段。
1.作一条线段等于已知线段
现在我们来解决这个问题。
作法:
(1)作射线AM
(2)在AM上截取AB= a。
则线段AB为所求。
应用:已知线段a、b,求作线段AB=a+b。
解:(1)作射线AM;
(2)在AM上顺次截取AC=a,CB= b。
则AB= a+b为所求。
做一做:作线段AB=a-b。
2、比较两条线段的长短
两条线段可能相等,也可能不相等,那么怎样比较两条线段的长短呢?
我们先来回答下面的问题。
怎样比较两个同学的身高?
一是用尺子测量;二是站在一起比(脚在同一高度)。
如果把两个同学看成两条线段,那么比较两条线段就有两种方法。
(1)度量法:用刻度尺分别量出两条线段的长度从而进行比较。
( 2)把一条线段移到另一条线段上,使一端对齐,从而进行比较,我们称为叠合法。(如图)
AB<CD AB>CD AB=CD
3、线段的中点及等分点
如图(1),点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点;
记作AM=MB或AM=MB=1/2AB或2AM=2MB=AB。
如图(2),点M、N把线段AB分成相等的三段AM、MN、NB,点M、N叫做线段AB的三等分点。类似地,还有四等分点,等等。4、线段的性质
请同学们思考课本131页的思考?
结论:
两点所连的线中,
简单地说成:___________________________________
你能举出这条性质在生活中的一些应用吗?
两点间的距离的定义:___________________________________
注意:距离是用“数”来度量的,它是线段的长度,而不是线段本身。
三、巩固提高
1、课本131页练习1、2
2、在直线上顺次取A、B、C三点,使 AB=4㎝,BC=3㎝,点O是线段AC的中点,则线段OB的长是〔 〕
A、2㎝ B、1.5㎝ C、0.5㎝ D、3.5㎝
3、已知线段AB=5㎝,C是直线AB上一点,若BC=2㎝,则线段AC的长为
四.、反思升华
1、把弯曲的河道改直后,缩短了河道的长度,这是因为 ;
2、已知,如图,AB=16㎝,C是BC的中点,且AC=10㎝,D是AC的中点,E是BC的中点,求线段DE的长。
第4课时 角与角的大小比较
任教者:高新球 王文昭 黄喜华 王安元
[学习目标]:
1.理解角、平角、周角的定义
2.能正确地表示角、会比较角的大小
3.认识角的平分线
重点:角的表示方法与大小比较
难点:角的表示方法
[学法指导]
自主学习 小组合作探究
[课前预习]
1、角的定义(1): 角是由有_________________的两条射线组成的图形,
这个公共端点是角的__________,这两条射线是角的_________________。
2、角的定义(2): 一条射线绕着它的_________从一个位置_________到另一位置时所成的图形叫做角。
3、角的大小由角的始边绕顶点旋转至终边时________________决定。
4、当射线绕着端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做_______角。
5、当射线绕着端点旋转一周,又重新回到原来的位置时,所成的角叫做______角。
[合作探究]
[活动一]:角的表示方法
1、如下图中的角,你能用几种方法把它表示出来?
[活动二]:角的大小比较方法
下面的三组图形,每组中都有两个角,你能判断它们的大小吗?说说你的方法.
[拓展延伸]:请同学们将手中的角对折,你发现了什么?
角的平分线:
如图,射线OP是∠AOB的角平分线,那么图这几个角
有怎样的大小关系?
2、如图,已知OB、OC是∠AOB的三等分线,试说出几个你能得到的正确结论:
第5课时 角的度量
任教者:高新球 王文昭 黄喜华 王安元
教学目的
1.理解1度的角的概念及角的分类。
2、理解余角及补角的概念及性质。
3、掌握角的大小的计算。
一、 自学自测
1、1度的角怎样定义: 。
2、角的换算单位:1°= ′= ″ 1″= ′= °
3、角的.分类
二、余角及补角的定义和性质:
1、互为余角和互为补角的概念
两角之和等于 度,这样的两个角叫做互为余角。
两角之和等于 度,这样的两个角叫做互为补角。
1)若∠1 + ∠2 =180 °, 则
2)若∠1和∠2互补,则 .
3)若∠3 + ∠4 =90 °,则 .
4)若∠3和∠4互余,则 .
2、互为余角及互为补角的性质
同角或等角的余角 ;同角或等角的补角 。
应用举例:∵∠1=∠2, ∠1+∠3=90°,∠ 2+∠4=90°(已知)
∴∠3=∠4(等角的余角相等)
填理由:∵∠1+∠2=180°,∠ 1+∠3=180°( )
∴∠3=∠4( )
3.如图,已知∠AOB与∠BOD互为余角,OC是∠BOD的角平分线,
∠AOB=29.66°,求∠COD的度数。
三、角的大小的计算:
1、70°39′的余角是 ,补角是 。
2、如果一个角的补角是150 ° ;那么这个角的余角是 。
3.根据图形填空:(1)∠DOB=∠DOC+∠
(2)∠AOD=∠DOB-∠ = -∠AOC
(3)∠DOC+∠BOA-∠DOB=
5.如图,若∠ABC=90 °,BP平分∠ ABD,
(1)若 ∠CBD=30° ,求∠ABP的度数。
(2)若∠CBD=x°,求∠ ABP的度数。
四 讨论更正 合作探究
五 小结:你学会了什么?
六 达标训练
1.∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.1)根据图形填空:
①∠DBA=∠DBC+
②∠DBC=∠DBP- =∠DBA-
③∠DBP+∠ABC-∠ABD=
2)变式:如图若∠ABC=90 ,∠CBD=30 ,你能求出哪些角的度数
第6课时 图形的认识总复习学案
任教者:高新球 王文昭 黄喜华 王安元
一、学习目标:(1)认识一些简单的几何体及其平面展开图。
(2)掌握“直线、射线、线段、角”这些基本图形的概念、性质、表示方法和画法。
(3)掌握线段中点、角平分线、互余(或互补)等概念,并会进行相关的推理和计算;
二、学习探索:
(一)平面图形与立体图形
1.下列物体:①圆筒形的易拉罐;②地球;③数学课本;④足球;⑤火柴盒;⑥文具盒中,形状类似于棱柱的有 (填写序号)
2.小亮为即将参加考试的好友小杰制作了一个正方体礼品盒(如图所示),六个面上各有一个字,连起来就是“预祝考试成功”,其中“预”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是( )
3埃及金字塔是世界奇迹之一,它充满了神秘与梦幻,请观察
如图所示的金字塔图片,试判断其形状类似于( )
A.圆柱 B.球 C.圆锥 D.棱锥
答案:(1)③⑤⑥;(2)C;(3)D;
(二)直线、射线、线段
1.下列说法:①射线MN与射线MP表示同一条射线;②平角是一条直线;③连接两点的线段长叫做这两点之间的距离;④若,则、和互为余角,其中错误的有( ) A.1个 B.2个 C.3个 D.4个
2.下列语句正确的是( ) A.画直线 B.角平分线是一条线段
C.画射线 D.延长线段AB到点C,使得
3.已知直线上有两点M、N,且,再找一点P,使,则P点的位置在( )。
A.直线上; B.直线外; C.直线上或直线外; D.不存在这一点P;
4.石匠师傅在用大理石铺地时,总是先在一侧的两头将两口根木棒插入地中,同时在中间拉上一根细线,铺地时沿着细线铺设,理由是 。
5.下列说法正确的是( )
A.直线的一半是射线; B.线段AB的长度就是A、B两间的距离;
C.直线上两点间的部分叫射线; D.若点P使,则点P是线段AB的中点;
6.如图,已知线段,点M为AB的中点,点P在MB上,点N为PB的中点,且。求PM的长。
7.在自来水主水管道AB的两旁有两个住宅小区C、D,现要在主水管道上开一个接水口P,往C、D两个小区铺设水管。为了节省铺水管的用料,
接口P应开在水管AB的什么位置?在图中画出来,
并说明依据的数学原理。
(三)角的度量与比较:
【基本知识点】
1.角的定义1:有 端点的两条 组成的图形叫角。其中公共端点叫角的 ,两条射线叫角的 .角的两条边是 线。
角的定义2:角也可以看作 而形成的图形;
2.角的度量单位之间的换算关系是: ;
3.从一个角的顶点出发,把这个角分成相等的两个角的射线,
叫做这个角的 。类似的还可以将角分成三等分、四等分。
几何语言表达: ∵如图,OC是∠AOB的平分线
∴= = ∠AOB 或 = =
4.如果两个角的和等于90°(直角),就说这两个角互为 ,通常记的余角是:
(用数学式表示);如果两个角的和等于180°(平角),就收这两个角互为 ,通常记:的补角是 (用数学式表示)。
补角性质:同角或等角的补角 ;余角性质:同角或等角的余角 。
纸盒
(1)长方体
(2)长方形
(3)正方形
(4)线段 点
建
设
和
谐
沾益
益
B BB
A
直线AB
·
·
a
直线a
O
b
a
点B在直线外
·
B BB
·
点A在直线上
A
·
a
·
B BB
A
O
A
m
·
②
①
A B C
A C D B
M
B
·
·
A
a
b
C
M
B
·
·
A
A(C)
B
(D)
A(C)
(D)
B
A(C)
B(D)
A
B
M
A
B
M
N
(1)
(2)
()
A
B
C
D
E
·
·
·
A
B
O
C
D
A
B
D
C
P
A
B
D
C
P
1 / 12
同课章节目录
