青岛版数学八年级下册6.3矩形的性质 教学设计(表格式)
文档属性
| 名称 | 青岛版数学八年级下册6.3矩形的性质 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 80.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 17:20:03 | ||
图片预览

文档简介
课题名称 矩形的性质 学科 数学
教师姓名 学生年级 八年级下 课时 1
教学目标 通过类比菱形的性质,探索、证明矩形的相关性质 能够利用矩形的性质,通过分析问题来解决简单的几何问题 通过探索矩形的性质,培养几何直观、逻辑分析等数学核心素养
教学重点 探究并掌握矩形的性质,能灵活运用解决实际问题
教学难点 矩形性质的探索及性质的灵活运用
教学策略的选择与设计 在菱形的性质探索的基础上,学生已经具备了自主学习的能力,所以本节课采用类比的方法从边、角、对角线及对称性的角度继续探究矩形的基本性质,让学生自主探究、合作探究,提升学生分析问题、解决问题的能力。 在设计上,将第一课时与第三课时性质部分题目相结合,提高学生的思维能力,提高课堂效率。
教学准备 PPT课件、几何画板、希沃授课助手
教学过程
学习目标 评价 任务 评价 标准 教 学 活 动
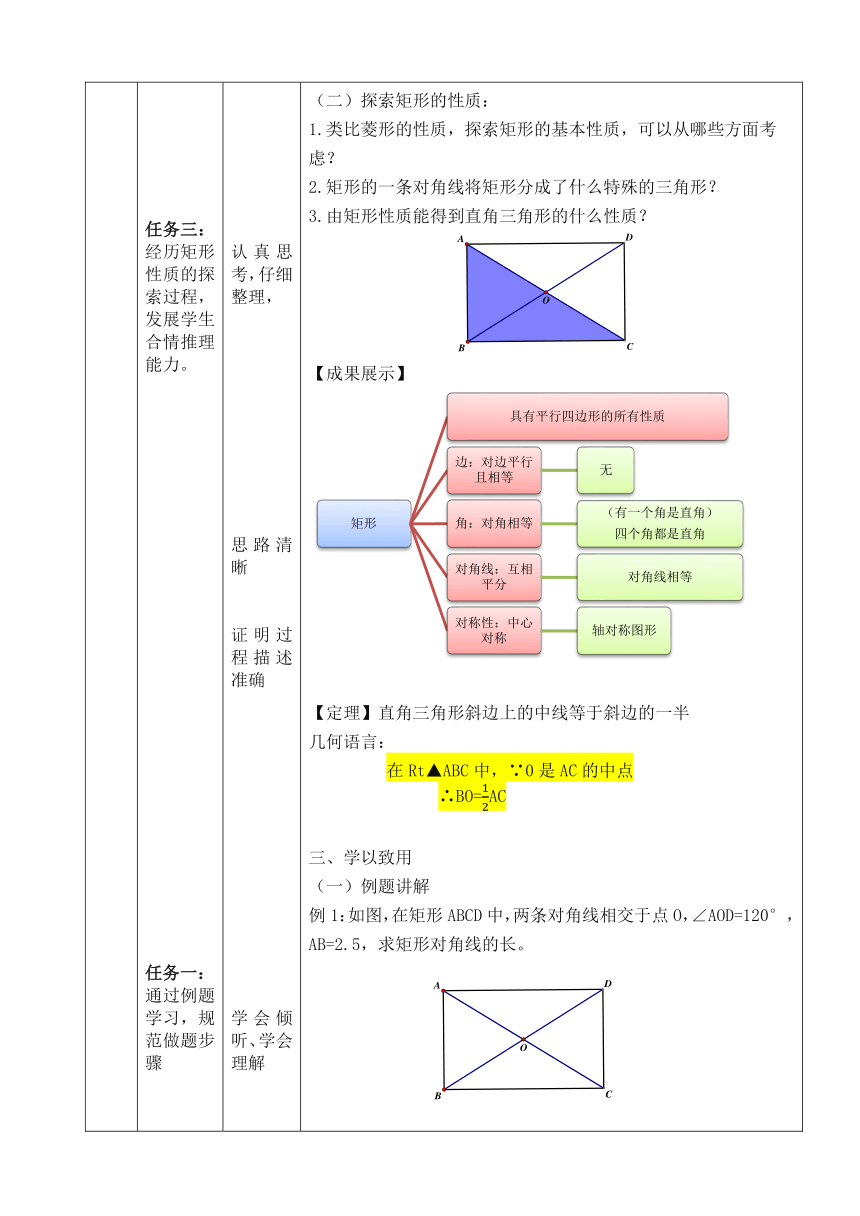
目标一:探索并掌握矩形的性质 目标二: 能准确应用菱形的性质解决简单的几何问题 任务一: 复习回顾平行四边形及菱形的基本性质 任务二: 掌握矩形的定义 任务三:经历矩形性质的探索过程,发展学生合情推理能力。 任务一: 通过例题学习,规范做题步骤 任务二: 能够直接利用矩形的性质解决问题 任务三: 能力提升 提升综合应用能力及分析分析问题解决问题的能力 从四个维度回答问题,回答准确、流畅 仔细观察,积极思考 认真思考,仔细整理, 思路清晰 证明过程描述准确 学会倾听、学会理解 书写规范、逻辑清晰,能够灵活准确表述所运用的知识 逻辑推理准确,几何语言规范 学生认真聆听 全身心投入,积极思考,认真钻研 积极参与小组活动,会倾听,懂分享 学会整理与反思 一、知识回顾 1.平行四边形的性质: 2.菱形的基本性质: 二、探索新知 平行四边形动态演示: 问题:从角的角度研究图形的变化,当改变∠1的大小时,你有什么发现? 结论: 矩形的定义:有一个角是直角的平行四边形是菱形 (二)探索矩形的性质: 1.类比菱形的性质,探索矩形的基本性质,可以从哪些方面考虑? 2.矩形的一条对角线将矩形分成了什么特殊的三角形? 3.由矩形性质能得到直角三角形的什么性质? 【成果展示】 【定理】直角三角形斜边上的中线等于斜边的一半 几何语言: 在Rt▲ABC中,∵0是AC的中点 ∴BO=AC 三、学以致用 (一)例题讲解 例1:如图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,求矩形对角线的长。 规范解题步骤: ∵四边形ABCD是矩形 ∴AC=BD ∵AO=CO=AC,BO=DO=BD ∴AO=BO=CO=DO 自主探究 1.如图,在矩形ABCD中,对角线AC与BD相交于点0.已知AB=6cm,AO=5cm,求BD与AD的长。 2.如图,在Rt▲ABC中,∠ACB=90°,D为AB的中点,AE//CD,CE//AB,试判断四边形ADCE的形状,并证明你的结论。 3【数学理解】: 已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,E,F分别是AC,BD的中点, 求证:EF⊥BD 【方法引领】 直角三角形,遇中点,构造斜边上的中线 (三)能力提升 例3 如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为点E,ED=3BE,求AE的长 【分析】由矩形的性质可得AO=BO=CO=DO,可得AE是BO的垂直平分线,故AB=AO,故▲ABO是等边三角形。在Rt▲AED中,应用30°所对直角边等于斜边的一半。 4.联系拓广 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为点E,F,求PE+PF的值 【方法点拨】 连接PO,在▲AOD中,利用等面积法求解
小结 1.矩形的定义 2.矩形的性质 3.直角三角形斜边上中线的性质
检测反馈 一个矩形的两条对角线的一个夹角为60°,对角线长为15,求矩形较短边的长
课后作业 1.必做(巩固类)《伴你学》第一课时 2.选做(动手操作类)用不同方法,利用直尺圆规做出一个菱形
教师姓名 学生年级 八年级下 课时 1
教学目标 通过类比菱形的性质,探索、证明矩形的相关性质 能够利用矩形的性质,通过分析问题来解决简单的几何问题 通过探索矩形的性质,培养几何直观、逻辑分析等数学核心素养
教学重点 探究并掌握矩形的性质,能灵活运用解决实际问题
教学难点 矩形性质的探索及性质的灵活运用
教学策略的选择与设计 在菱形的性质探索的基础上,学生已经具备了自主学习的能力,所以本节课采用类比的方法从边、角、对角线及对称性的角度继续探究矩形的基本性质,让学生自主探究、合作探究,提升学生分析问题、解决问题的能力。 在设计上,将第一课时与第三课时性质部分题目相结合,提高学生的思维能力,提高课堂效率。
教学准备 PPT课件、几何画板、希沃授课助手
教学过程
学习目标 评价 任务 评价 标准 教 学 活 动
目标一:探索并掌握矩形的性质 目标二: 能准确应用菱形的性质解决简单的几何问题 任务一: 复习回顾平行四边形及菱形的基本性质 任务二: 掌握矩形的定义 任务三:经历矩形性质的探索过程,发展学生合情推理能力。 任务一: 通过例题学习,规范做题步骤 任务二: 能够直接利用矩形的性质解决问题 任务三: 能力提升 提升综合应用能力及分析分析问题解决问题的能力 从四个维度回答问题,回答准确、流畅 仔细观察,积极思考 认真思考,仔细整理, 思路清晰 证明过程描述准确 学会倾听、学会理解 书写规范、逻辑清晰,能够灵活准确表述所运用的知识 逻辑推理准确,几何语言规范 学生认真聆听 全身心投入,积极思考,认真钻研 积极参与小组活动,会倾听,懂分享 学会整理与反思 一、知识回顾 1.平行四边形的性质: 2.菱形的基本性质: 二、探索新知 平行四边形动态演示: 问题:从角的角度研究图形的变化,当改变∠1的大小时,你有什么发现? 结论: 矩形的定义:有一个角是直角的平行四边形是菱形 (二)探索矩形的性质: 1.类比菱形的性质,探索矩形的基本性质,可以从哪些方面考虑? 2.矩形的一条对角线将矩形分成了什么特殊的三角形? 3.由矩形性质能得到直角三角形的什么性质? 【成果展示】 【定理】直角三角形斜边上的中线等于斜边的一半 几何语言: 在Rt▲ABC中,∵0是AC的中点 ∴BO=AC 三、学以致用 (一)例题讲解 例1:如图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,求矩形对角线的长。 规范解题步骤: ∵四边形ABCD是矩形 ∴AC=BD ∵AO=CO=AC,BO=DO=BD ∴AO=BO=CO=DO 自主探究 1.如图,在矩形ABCD中,对角线AC与BD相交于点0.已知AB=6cm,AO=5cm,求BD与AD的长。 2.如图,在Rt▲ABC中,∠ACB=90°,D为AB的中点,AE//CD,CE//AB,试判断四边形ADCE的形状,并证明你的结论。 3【数学理解】: 已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,E,F分别是AC,BD的中点, 求证:EF⊥BD 【方法引领】 直角三角形,遇中点,构造斜边上的中线 (三)能力提升 例3 如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为点E,ED=3BE,求AE的长 【分析】由矩形的性质可得AO=BO=CO=DO,可得AE是BO的垂直平分线,故AB=AO,故▲ABO是等边三角形。在Rt▲AED中,应用30°所对直角边等于斜边的一半。 4.联系拓广 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为点E,F,求PE+PF的值 【方法点拨】 连接PO,在▲AOD中,利用等面积法求解
小结 1.矩形的定义 2.矩形的性质 3.直角三角形斜边上中线的性质
检测反馈 一个矩形的两条对角线的一个夹角为60°,对角线长为15,求矩形较短边的长
课后作业 1.必做(巩固类)《伴你学》第一课时 2.选做(动手操作类)用不同方法,利用直尺圆规做出一个菱形
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
