12.2全等三角形的判定(1) 教案(表格式) 2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 12.2全等三角形的判定(1) 教案(表格式) 2023-2024学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 105.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 00:00:00 | ||
图片预览

文档简介
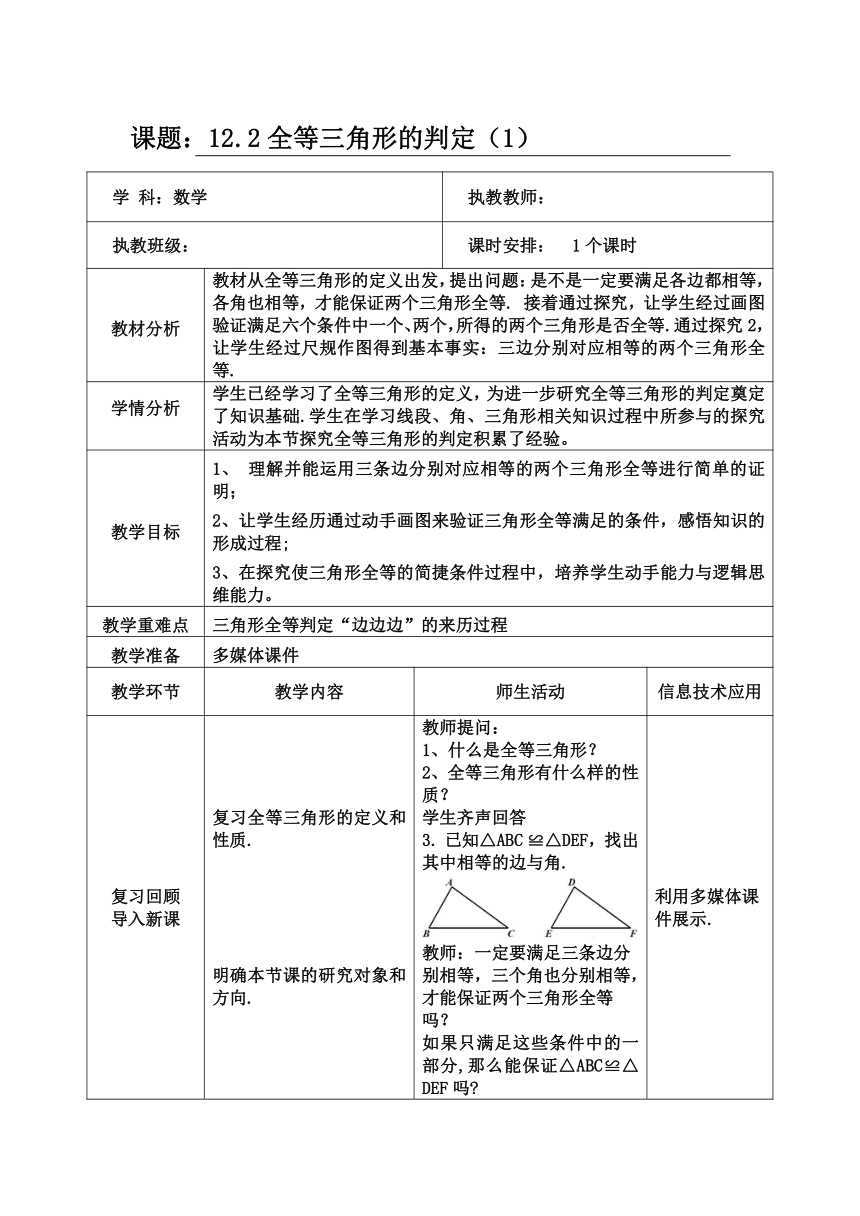
课题:12.2全等三角形的判定(1)
学 科:数学 执教教师:
执教班级: 课时安排: 1个课时
教材分析 教材从全等三角形的定义出发,提出问题:是不是一定要满足各边都相等,各角也相等,才能保证两个三角形全等. 接着通过探究,让学生经过画图验证满足六个条件中一个、两个,所得的两个三角形是否全等.通过探究2,让学生经过尺规作图得到基本事实:三边分别对应相等的两个三角形全等.
学情分析 学生已经学习了全等三角形的定义,为进一步研究全等三角形的判定奠定了知识基础.学生在学习线段、角、三角形相关知识过程中所参与的探究活动为本节探究全等三角形的判定积累了经验。
教学目标 1、 理解并能运用三条边分别对应相等的两个三角形全等进行简单的证明; 2、让学生经历通过动手画图来验证三角形全等满足的条件,感悟知识的形成过程; 3、在探究使三角形全等的简捷条件过程中,培养学生动手能力与逻辑思维能力。
教学重难点 三角形全等判定“边边边”的来历过程
教学准备 多媒体课件
教学环节 教学内容 师生活动 信息技术应用
复习回顾 导入新课 复习全等三角形的定义和性质. 明确本节课的研究对象和方向. 教师提问: 1、什么是全等三角形? 2、全等三角形有什么样的性质? 学生齐声回答 已知△ABC ≌△DEF,找出其中相等的边与角. 教师:一定要满足三条边分别相等,三个角也分别相等,才能保证两个三角形全等吗? 如果只满足这些条件中的一部分,那么能保证△ABC≌△DEF吗 利用多媒体课件展示.
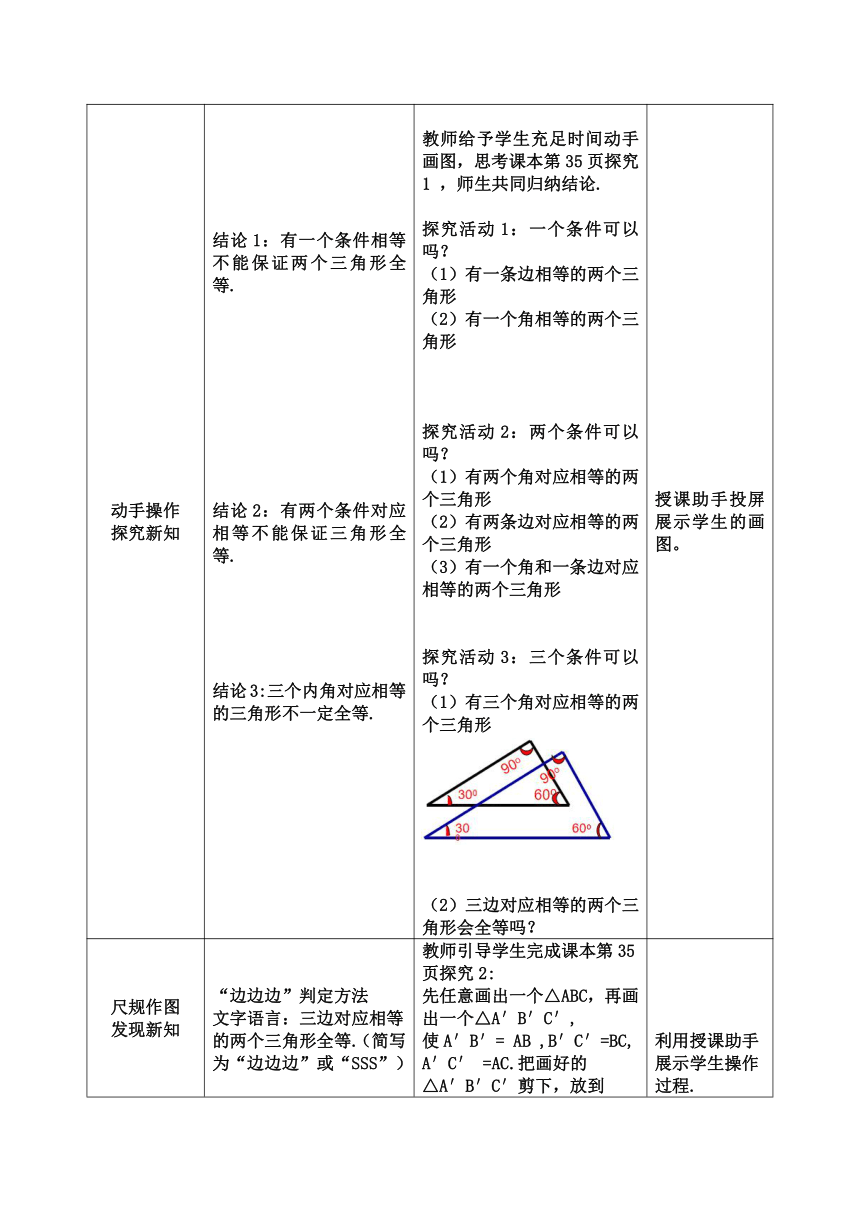
动手操作 探究新知 结论1:有一个条件相等不能保证两个三角形全等. 结论2:有两个条件对应相等不能保证三角形全等. 结论3:三个内角对应相等的三角形不一定全等. 教师给予学生充足时间动手画图,思考课本第35页探究1 ,师生共同归纳结论. 探究活动1:一个条件可以吗? (1)有一条边相等的两个三角形 (2)有一个角相等的两个三角形 探究活动2:两个条件可以吗? (1)有两个角对应相等的两个三角形 (2)有两条边对应相等的两个三角形 (3)有一个角和一条边对应相等的两个三角形 探究活动3:三个条件可以吗? (1)有三个角对应相等的两个三角形 (2)三边对应相等的两个三角形会全等吗? 授课助手投屏展示学生的画图。
尺规作图 发现新知 “边边边”判定方法 文字语言:三边对应相等的两个三角形全等.(简写为“边边边”或“SSS”) 几何语言: 教师引导学生完成课本第35页探究2: 先任意画出一个△ABC,再画出一个△A′B′C′, 使A′B′= AB ,B′C′=BC, A′C′ =AC.把画好的 △A′B′C′剪下,放到 △ABC上,他们全等吗? 教师在黑板上画图,并说出作法: (1)画B′C′=BC; (2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A'; (3)连接线段A'B',A 'C '. 想一想:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗? 利用授课助手展示学生操作过程. 使用班级优化大师抽选与点评.
典例讲解 应用所学 例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.求证:(1)△ABD ≌△ACD ;(2)∠BAD = ∠CAD. 证明的书写步骤: ①准备条件:证全等时要用的条件要先证好; ②指明范围:写出在哪两个三角形中; ③摆齐根据:摆出三个条件用大括号括起来; ④写出结论:写出全等结论. 例2 用尺规作一个角等于已知角. 已知:∠AOB.求作:∠A′O′B′=∠AOB. 教师给予学生充足时间思考 ,当部分学生解题有困难时,教师给出本题的解题思路. 师生共同完成解答. 教师指导学生完成作图. 作法: (1)以点O 为圆心,任意长为半径画弧,分别交OA, OB 于点C、D; (2)画一条射线O′A′,以点O′为圆心,OC 长为半 径画弧,交O′A′于点C′; (3)以点C′为圆心,CD 长为半径画弧,与第2 步中 所画的弧交于点D′; (4)过点D′画射线O′B′,则∠A′O′B′=∠AOB. 授课助手投屏展示 使用课件中动画演示.
课堂练习 巩固新知 1.如图, C是BF的中点,AB =DC,AC=DF. 求证:△ABC ≌ △DCF. 2、课本练习2 教师给予学生充足时间思考并在稿纸上写出过程,挑选优秀作业投屏展示. 教师抽选学生回答,并说明理由. 班级优化大师随机抽选、小组点评.
反思回顾 归纳总结 ①本节课,我学到了哪些知识? ②本节课,给我感受最深的是什么? ③课后你准备对哪方面进行进一步研究? 还有哪些困惑?此外我还知道了…… 教师让学生通过问题回忆课堂内容,找出不足,为进一步研究提供契机. 课件展示
学情反馈 布置作业 1.课堂作业: 课本 第43页第1、2题; 2.家庭作业: 完成基训本课时练习. 学生课后完成,教师批改、讲评.
学 科:数学 执教教师:
执教班级: 课时安排: 1个课时
教材分析 教材从全等三角形的定义出发,提出问题:是不是一定要满足各边都相等,各角也相等,才能保证两个三角形全等. 接着通过探究,让学生经过画图验证满足六个条件中一个、两个,所得的两个三角形是否全等.通过探究2,让学生经过尺规作图得到基本事实:三边分别对应相等的两个三角形全等.
学情分析 学生已经学习了全等三角形的定义,为进一步研究全等三角形的判定奠定了知识基础.学生在学习线段、角、三角形相关知识过程中所参与的探究活动为本节探究全等三角形的判定积累了经验。
教学目标 1、 理解并能运用三条边分别对应相等的两个三角形全等进行简单的证明; 2、让学生经历通过动手画图来验证三角形全等满足的条件,感悟知识的形成过程; 3、在探究使三角形全等的简捷条件过程中,培养学生动手能力与逻辑思维能力。
教学重难点 三角形全等判定“边边边”的来历过程
教学准备 多媒体课件
教学环节 教学内容 师生活动 信息技术应用
复习回顾 导入新课 复习全等三角形的定义和性质. 明确本节课的研究对象和方向. 教师提问: 1、什么是全等三角形? 2、全等三角形有什么样的性质? 学生齐声回答 已知△ABC ≌△DEF,找出其中相等的边与角. 教师:一定要满足三条边分别相等,三个角也分别相等,才能保证两个三角形全等吗? 如果只满足这些条件中的一部分,那么能保证△ABC≌△DEF吗 利用多媒体课件展示.
动手操作 探究新知 结论1:有一个条件相等不能保证两个三角形全等. 结论2:有两个条件对应相等不能保证三角形全等. 结论3:三个内角对应相等的三角形不一定全等. 教师给予学生充足时间动手画图,思考课本第35页探究1 ,师生共同归纳结论. 探究活动1:一个条件可以吗? (1)有一条边相等的两个三角形 (2)有一个角相等的两个三角形 探究活动2:两个条件可以吗? (1)有两个角对应相等的两个三角形 (2)有两条边对应相等的两个三角形 (3)有一个角和一条边对应相等的两个三角形 探究活动3:三个条件可以吗? (1)有三个角对应相等的两个三角形 (2)三边对应相等的两个三角形会全等吗? 授课助手投屏展示学生的画图。
尺规作图 发现新知 “边边边”判定方法 文字语言:三边对应相等的两个三角形全等.(简写为“边边边”或“SSS”) 几何语言: 教师引导学生完成课本第35页探究2: 先任意画出一个△ABC,再画出一个△A′B′C′, 使A′B′= AB ,B′C′=BC, A′C′ =AC.把画好的 △A′B′C′剪下,放到 △ABC上,他们全等吗? 教师在黑板上画图,并说出作法: (1)画B′C′=BC; (2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A'; (3)连接线段A'B',A 'C '. 想一想:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗? 利用授课助手展示学生操作过程. 使用班级优化大师抽选与点评.
典例讲解 应用所学 例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.求证:(1)△ABD ≌△ACD ;(2)∠BAD = ∠CAD. 证明的书写步骤: ①准备条件:证全等时要用的条件要先证好; ②指明范围:写出在哪两个三角形中; ③摆齐根据:摆出三个条件用大括号括起来; ④写出结论:写出全等结论. 例2 用尺规作一个角等于已知角. 已知:∠AOB.求作:∠A′O′B′=∠AOB. 教师给予学生充足时间思考 ,当部分学生解题有困难时,教师给出本题的解题思路. 师生共同完成解答. 教师指导学生完成作图. 作法: (1)以点O 为圆心,任意长为半径画弧,分别交OA, OB 于点C、D; (2)画一条射线O′A′,以点O′为圆心,OC 长为半 径画弧,交O′A′于点C′; (3)以点C′为圆心,CD 长为半径画弧,与第2 步中 所画的弧交于点D′; (4)过点D′画射线O′B′,则∠A′O′B′=∠AOB. 授课助手投屏展示 使用课件中动画演示.
课堂练习 巩固新知 1.如图, C是BF的中点,AB =DC,AC=DF. 求证:△ABC ≌ △DCF. 2、课本练习2 教师给予学生充足时间思考并在稿纸上写出过程,挑选优秀作业投屏展示. 教师抽选学生回答,并说明理由. 班级优化大师随机抽选、小组点评.
反思回顾 归纳总结 ①本节课,我学到了哪些知识? ②本节课,给我感受最深的是什么? ③课后你准备对哪方面进行进一步研究? 还有哪些困惑?此外我还知道了…… 教师让学生通过问题回忆课堂内容,找出不足,为进一步研究提供契机. 课件展示
学情反馈 布置作业 1.课堂作业: 课本 第43页第1、2题; 2.家庭作业: 完成基训本课时练习. 学生课后完成,教师批改、讲评.
