12.2全等三角形的判定(3) 教案(表格式) 2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 12.2全等三角形的判定(3) 教案(表格式) 2023-2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 185.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 00:00:00 | ||
图片预览

文档简介
课题:12.2全等三角形的判定(3)
学 科:数学 执教教师:
执教班级: 课时安排: 1个课时
教材分析 教材对“角边角”判定方法的处理与“边边边”“边角边”判定方法类似,即先通过探究4中的作图实验操作,让学生经历探究过程,然后在让学生总结探究出的规律后,直接以基本事实的方式给出“角边角”判定方法.
学情分析 学生在学习“边边边”“边角边”判定方法时,经历了作图实验操作、总结探究规律的学习过程,为本节课探究“角边角”的学习积累了经验。
教学目标 1、 理解并能运用“角边角”“角角边”的全等三角形判定方法并能进行简单的证明; 2、让学生经历通过动手画图来验证三角形全等满足的条件,感悟知识的形成过程; 3、在探究三角形全等判定方法的过程中,培养学生动手能力与逻辑思维能力。
教学重难点 理解并能运用“角边角”“角角边”
教学准备 多媒体课件
教学环节 教学内容 师生活动 信息技术应用
课前练习 复习引入 复习已经学过的全等三角形判定方法“边边边”“边角边”. 提出本节课的研究对象 教师出示问题: 1、已知BD=CD,要判定△ABD ≌ △ACD,则还需要添加的条件是_____________。 2、要判定△ABD ≌ △ACD, (1)请你给出合适的条件______ 、_______; (2)除(1)中给出的条件外,还可以给其他的条件吗?(比如给的都是角) 利用多媒体课件展示.
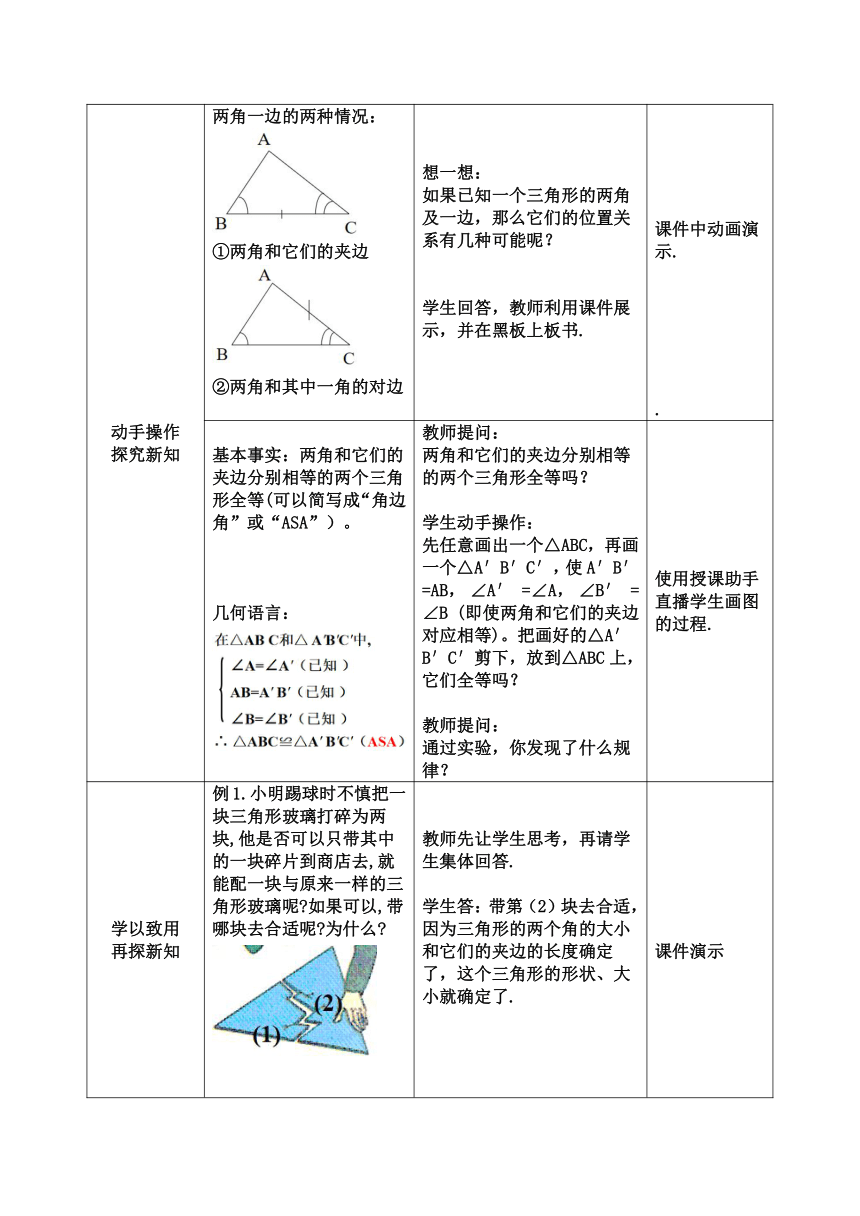
动手操作 探究新知 两角一边的两种情况: ①两角和它们的夹边 ②两角和其中一角的对边 想一想: 如果已知一个三角形的两角及一边,那么它们的位置关系有几种可能呢? 学生回答,教师利用课件展示,并在黑板上板书. 课件中动画演示. .
基本事实:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”)。 几何语言: 教师提问: 两角和它们的夹边分别相等的两个三角形全等吗? 学生动手操作: 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB, ∠A′ =∠A, ∠B′ =∠B (即使两角和它们的夹边对应相等)。把画好的△A′B′C′剪下,放到△ABC上,它们全等吗? 教师提问: 通过实验,你发现了什么规律? 使用授课助手直播学生画图的过程.
学以致用 再探新知 例1.小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢 如果可以,带哪块去合适呢 为什么 例2.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:AD=AE. 教师先让学生思考,再请学生集体回答. 学生答:带第(2)块去合适, 因为三角形的两个角的大小和它们的夹边的长度确定了,这个三角形的形状、大小就确定了. 教师给予学生充足时间在草稿纸上完成解答. 教师给出正确的解答过程: 教师点拨: 在两个三角形中要证明边相等、角相等,我们通常是证明两个三角形全等; 2、当题目中显性条件不够时,我们要注意观察图形,找出其中的隐含条件。 课件演示 使用授课助手投屏展示.
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”). 几何语言: 教师提问: 两角和其中一角的对边分别相等的两个三角形全等吗? 如下图,在△ABC和△DEF中,∠A =∠D, ∠ B=∠E, BC=EF, 求证△ABC与△DEF全等。 教师让学思考,并完成解答, 投屏展示学生的证明. 课件中动画演示.
课堂练习 巩固新知 如图,已知∠1=∠2, ∠3=∠4,BD=CE. 求证:AB=AC 要判定△ABD ≌ △ACD ,请你给出合适的条件_____、 ____ 。(不再加边) 教师给予学生充足时间在稿纸上完成解答,然后投屏展示学生的解答,并作评析. 教师让学生自由思考、小组讨论,鼓励学生说出不同的答案,并说明理由. 使用授课助手投屏展示. 班级优化大师随机抽选、小组点评.
反思回顾 归纳总结 ①本节课,我学到了哪些知识? ②本节课,给我感受最深的是什么? ③课后你准备对哪方面进行进一步研究? 还有哪些困惑?此外我还知道了…… 教师让学生通过问题回忆课堂内容,找出不足,为进一步研究提供契机. 课件展示
学情反馈 布置作业 1.课堂作业: 课本 第44页第4、5题; 2.家庭作业: 完成基训本课时习题 学生课后完成,教师批改、讲评.
学 科:数学 执教教师:
执教班级: 课时安排: 1个课时
教材分析 教材对“角边角”判定方法的处理与“边边边”“边角边”判定方法类似,即先通过探究4中的作图实验操作,让学生经历探究过程,然后在让学生总结探究出的规律后,直接以基本事实的方式给出“角边角”判定方法.
学情分析 学生在学习“边边边”“边角边”判定方法时,经历了作图实验操作、总结探究规律的学习过程,为本节课探究“角边角”的学习积累了经验。
教学目标 1、 理解并能运用“角边角”“角角边”的全等三角形判定方法并能进行简单的证明; 2、让学生经历通过动手画图来验证三角形全等满足的条件,感悟知识的形成过程; 3、在探究三角形全等判定方法的过程中,培养学生动手能力与逻辑思维能力。
教学重难点 理解并能运用“角边角”“角角边”
教学准备 多媒体课件
教学环节 教学内容 师生活动 信息技术应用
课前练习 复习引入 复习已经学过的全等三角形判定方法“边边边”“边角边”. 提出本节课的研究对象 教师出示问题: 1、已知BD=CD,要判定△ABD ≌ △ACD,则还需要添加的条件是_____________。 2、要判定△ABD ≌ △ACD, (1)请你给出合适的条件______ 、_______; (2)除(1)中给出的条件外,还可以给其他的条件吗?(比如给的都是角) 利用多媒体课件展示.
动手操作 探究新知 两角一边的两种情况: ①两角和它们的夹边 ②两角和其中一角的对边 想一想: 如果已知一个三角形的两角及一边,那么它们的位置关系有几种可能呢? 学生回答,教师利用课件展示,并在黑板上板书. 课件中动画演示. .
基本事实:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”)。 几何语言: 教师提问: 两角和它们的夹边分别相等的两个三角形全等吗? 学生动手操作: 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB, ∠A′ =∠A, ∠B′ =∠B (即使两角和它们的夹边对应相等)。把画好的△A′B′C′剪下,放到△ABC上,它们全等吗? 教师提问: 通过实验,你发现了什么规律? 使用授课助手直播学生画图的过程.
学以致用 再探新知 例1.小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢 如果可以,带哪块去合适呢 为什么 例2.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:AD=AE. 教师先让学生思考,再请学生集体回答. 学生答:带第(2)块去合适, 因为三角形的两个角的大小和它们的夹边的长度确定了,这个三角形的形状、大小就确定了. 教师给予学生充足时间在草稿纸上完成解答. 教师给出正确的解答过程: 教师点拨: 在两个三角形中要证明边相等、角相等,我们通常是证明两个三角形全等; 2、当题目中显性条件不够时,我们要注意观察图形,找出其中的隐含条件。 课件演示 使用授课助手投屏展示.
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”). 几何语言: 教师提问: 两角和其中一角的对边分别相等的两个三角形全等吗? 如下图,在△ABC和△DEF中,∠A =∠D, ∠ B=∠E, BC=EF, 求证△ABC与△DEF全等。 教师让学思考,并完成解答, 投屏展示学生的证明. 课件中动画演示.
课堂练习 巩固新知 如图,已知∠1=∠2, ∠3=∠4,BD=CE. 求证:AB=AC 要判定△ABD ≌ △ACD ,请你给出合适的条件_____、 ____ 。(不再加边) 教师给予学生充足时间在稿纸上完成解答,然后投屏展示学生的解答,并作评析. 教师让学生自由思考、小组讨论,鼓励学生说出不同的答案,并说明理由. 使用授课助手投屏展示. 班级优化大师随机抽选、小组点评.
反思回顾 归纳总结 ①本节课,我学到了哪些知识? ②本节课,给我感受最深的是什么? ③课后你准备对哪方面进行进一步研究? 还有哪些困惑?此外我还知道了…… 教师让学生通过问题回忆课堂内容,找出不足,为进一步研究提供契机. 课件展示
学情反馈 布置作业 1.课堂作业: 课本 第44页第4、5题; 2.家庭作业: 完成基训本课时习题 学生课后完成,教师批改、讲评.
