第11章 课题学习《数学活动:平面镶嵌》 教案(表格式) 2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 第11章 课题学习《数学活动:平面镶嵌》 教案(表格式) 2023-2024学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 180.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 18:09:55 | ||
图片预览

文档简介
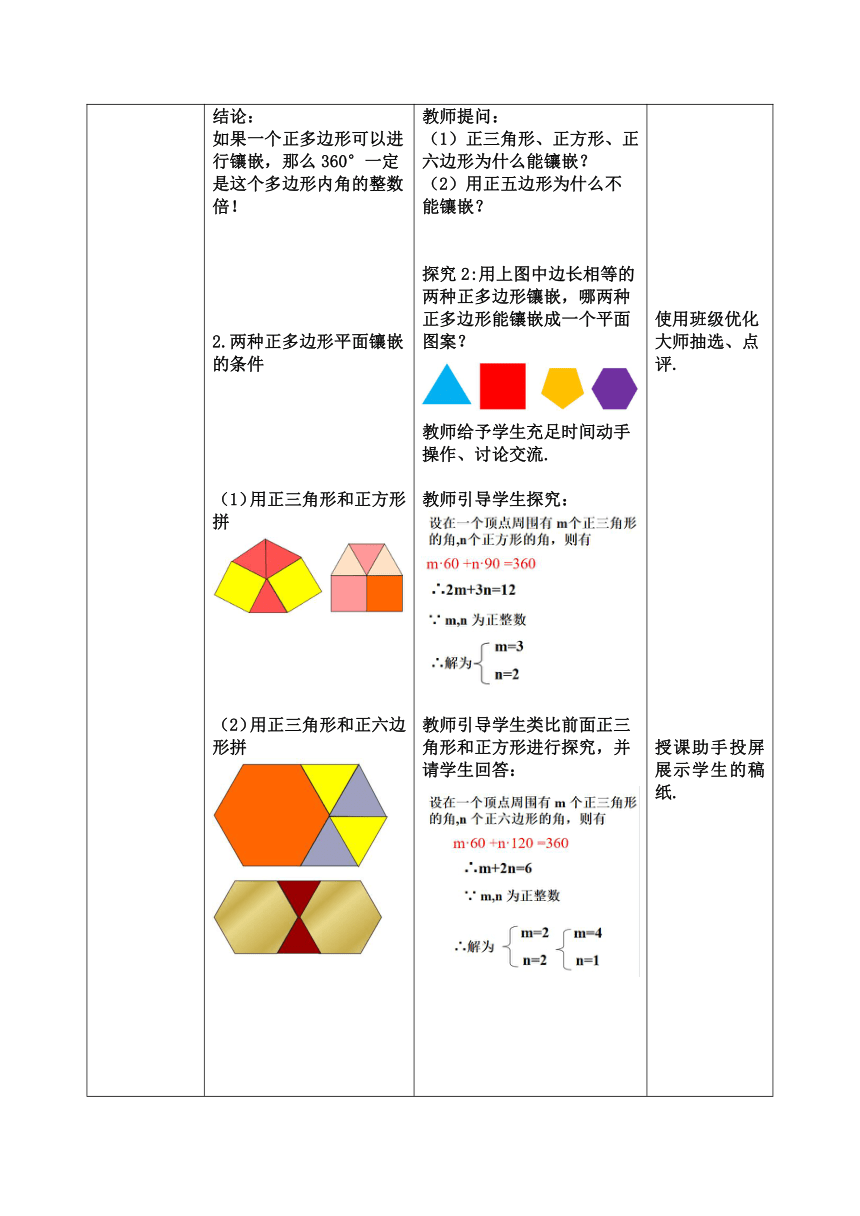
课题:实验、猜想、证明
学 科:数学 执教教师:
执教班级: 课时安排: 1个课时
教学目标 1.了解平面镶嵌的概念,弄清平面镶嵌的条件. 2.通过探究多边形镶嵌的过程,发展学生的动手能力,合情推理能力,合作能力等.
教学重难点 通过构建方程归纳两种正多边形镶嵌的条件.
教学准备 多媒体课件
教学环节 教学内容 师生活动 信息技术应用
图片欣赏 发现新知 欣赏生活中的平面镶嵌图片 从数学角度看,用一些不重叠摆放的图形把平面的一部分完全覆盖,通常把这类问题叫做覆盖平面(或平面镶嵌)的问题 教师提问:通过观察下面的图片,你发现它们有哪些共同特征? 教师引导,学生回答: 不重叠 2.完全覆盖 教师呈现平面镶嵌的概念. 利用课件动画呈现图片.
小组研学 探究新知 1.一种正多边形平面镶嵌的条件 结论: 如果一个正多边形可以进行镶嵌,那么360°一定是这个多边形内角的整数倍! 2.两种正多边形平面镶嵌的条件 (1)用正三角形和正方形拼 (2)用正三角形和正六边形拼 (3)用正方形和正六边形拼 (4)其他情况 用两种正多边形镶嵌的规律: 拼接在同一个点的各个角的和恰好等于360°(周角)。 3.任意相同三角形或四边形的平面镶嵌 多边形镶嵌的条件: 拼接在同一个顶点处的各个多边形的内角之和等于360° 探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案? 教师给予学生时间思考. 教师利用动画演示拼图. 教师提问: 正三角形、正方形、正六边形为什么能镶嵌? 用正五边形为什么不能镶嵌? 探究2:用上图中边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案? 教师给予学生充足时间动手操作、讨论交流. 教师引导学生探究: 教师引导学生类比前面正三角形和正方形进行探究,并请学生回答: 师生合作完成: 设在一个顶点周围有 m 个正方形的角,n 个正六边形的角,则有: m·90 +n·120 =360 ∴3m+4n=12 ∵ m,n 为正整数 ∴无解 ∴用正方形和正六边形不可以平面镶嵌 探究3:用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢? 教师给予学生时间思考,待学生作答后,教师利用ppt动画演示拼图。 授课助手投屏展示. 使用班级优化大师抽选、点评. 授课助手投屏展示学生的稿纸. PPT课件动画演示.
反思回顾 归纳总结 ①本节课,我学到了哪些知识? ②本节课,给我感受最深的是什么? ③课后你准备对哪方面进行进一步研究? 还有哪些困惑?此外我还知道了…… 教师让学生通过问题回忆课堂内容,找出不足,为进一步研究提供契机.
布置作业 学情反馈 先让学生们欣赏一组美丽的图片,然后布置作业: 课下设计一幅多边形镶嵌的美丽图案 ,看谁的设计最有新意 ! 学生课后完成,教师将优秀作品投屏展示.
学 科:数学 执教教师:
执教班级: 课时安排: 1个课时
教学目标 1.了解平面镶嵌的概念,弄清平面镶嵌的条件. 2.通过探究多边形镶嵌的过程,发展学生的动手能力,合情推理能力,合作能力等.
教学重难点 通过构建方程归纳两种正多边形镶嵌的条件.
教学准备 多媒体课件
教学环节 教学内容 师生活动 信息技术应用
图片欣赏 发现新知 欣赏生活中的平面镶嵌图片 从数学角度看,用一些不重叠摆放的图形把平面的一部分完全覆盖,通常把这类问题叫做覆盖平面(或平面镶嵌)的问题 教师提问:通过观察下面的图片,你发现它们有哪些共同特征? 教师引导,学生回答: 不重叠 2.完全覆盖 教师呈现平面镶嵌的概念. 利用课件动画呈现图片.
小组研学 探究新知 1.一种正多边形平面镶嵌的条件 结论: 如果一个正多边形可以进行镶嵌,那么360°一定是这个多边形内角的整数倍! 2.两种正多边形平面镶嵌的条件 (1)用正三角形和正方形拼 (2)用正三角形和正六边形拼 (3)用正方形和正六边形拼 (4)其他情况 用两种正多边形镶嵌的规律: 拼接在同一个点的各个角的和恰好等于360°(周角)。 3.任意相同三角形或四边形的平面镶嵌 多边形镶嵌的条件: 拼接在同一个顶点处的各个多边形的内角之和等于360° 探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案? 教师给予学生时间思考. 教师利用动画演示拼图. 教师提问: 正三角形、正方形、正六边形为什么能镶嵌? 用正五边形为什么不能镶嵌? 探究2:用上图中边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案? 教师给予学生充足时间动手操作、讨论交流. 教师引导学生探究: 教师引导学生类比前面正三角形和正方形进行探究,并请学生回答: 师生合作完成: 设在一个顶点周围有 m 个正方形的角,n 个正六边形的角,则有: m·90 +n·120 =360 ∴3m+4n=12 ∵ m,n 为正整数 ∴无解 ∴用正方形和正六边形不可以平面镶嵌 探究3:用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢? 教师给予学生时间思考,待学生作答后,教师利用ppt动画演示拼图。 授课助手投屏展示. 使用班级优化大师抽选、点评. 授课助手投屏展示学生的稿纸. PPT课件动画演示.
反思回顾 归纳总结 ①本节课,我学到了哪些知识? ②本节课,给我感受最深的是什么? ③课后你准备对哪方面进行进一步研究? 还有哪些困惑?此外我还知道了…… 教师让学生通过问题回忆课堂内容,找出不足,为进一步研究提供契机.
布置作业 学情反馈 先让学生们欣赏一组美丽的图片,然后布置作业: 课下设计一幅多边形镶嵌的美丽图案 ,看谁的设计最有新意 ! 学生课后完成,教师将优秀作品投屏展示.
