人教版小学数学六年级上册 3 .5《解决实际问题》教案+任务单+练习(无答案)
文档属性
| 名称 | 人教版小学数学六年级上册 3 .5《解决实际问题》教案+任务单+练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-25 19:34:58 | ||
图片预览



文档简介
教学设计
课程基本信息
学科 数学 年级 六年级 学期 秋季
课题 解决实际问题(第5课时)
教科书 书 名:义务教育教科书数学 出版社:人民教育出版社 出版日期:2022年8月
教学目标
1.进一步理解分数除法解决问题的几种类型,能根据题目的特点,选择合适的方法解决问题。 2.通过辨析比较,寻找知识之间的内在联系,进一步体会方程思想在数学中的应用,在解决问题的过程中建立数学模型,提高学生解决问题的能力。 3.感受数学与生活的联系,体会探究数学的乐趣。
教学内容
教学重点: 沟通知识间的联系,体会方程思想的优势,建立数学模型。 教学难点: 体会方程思想的优势,建立数学模型。
教学过程
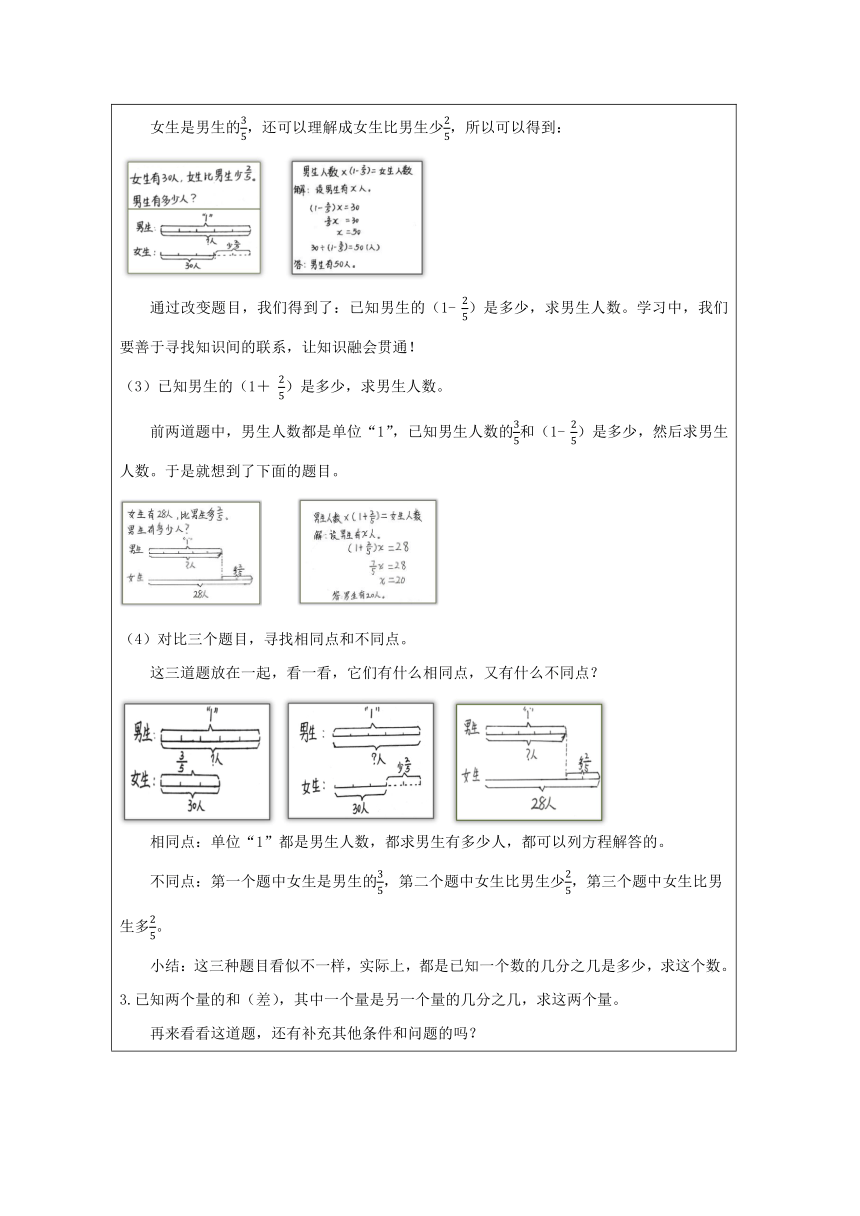
一、谈话引入 在前几节课的学习中,同学们利用方程解决了一些有关分数除法的实际问题,今天我们来上一节练习课。 二、学习交流中,深入理解知识 (一)分析关键信息 1.出示信息:女生人数是男生人数的。 从这句话中,你能分析出什么信息? 2.学生分析信息。 如:男生人数是单位“1”,把男生人数平均分成5份,女生人数是这样的3份。男生人数比女生人数多2份,男女生人数一共可以有8份;女生人数是所有人数的,男生人数是所有人数的 等等。 (二)补充条件,形成实际问题 1.学生讨论可以补充什么条件。 如果让同学们补充一个条件,把它变成学过的数学问题,想一想,可以补充什么条件? 学生思考,说一说可以补充什么条件。 比如:补充男生或女生的人数、男生和女生的总人数、男生和女生的人数差。在补充条件的过程中,引导学生观察数据的特点,选择合适的数据。 2.学生补充条件和问题,尝试解答。 听了前面几位同学的发言,相信大家都有了自己的想法。请你也补充上合适的条件和问题,并尝试解答。 (三)对比、辨析中,加深对知识的理解 1.已知单位“1”的数量,求单位“1”的几分之几是多少。 通过补充条件,把这道题变成了用分数乘法解决的实际问题。 2.已知单位“1”的几分之几是多少,求单位“1”的数量。 (1)已知男生的是多少,求男生人数。 (2)已知男生的(1- )是多少,求男生人数。 女生是男生的,还可以理解成女生比男生少,所以可以得到: 通过改变题目,我们得到了:已知男生的(1-)是多少,求男生人数。学习中,我们要善于寻找知识间的联系,让知识融会贯通! (3)已知男生的(1+ )是多少,求男生人数。 前两道题中,男生人数都是单位“1”,已知男生人数的和(1-)是多少,然后求男生人数。于是就想到了下面的题目。 (4)对比三个题目,寻找相同点和不同点。 这三道题放在一起,看一看,它们有什么相同点,又有什么不同点? 相同点:单位“1”都是男生人数,都求男生有多少人,都可以列方程解答的。 不同点:第一个题中女生是男生的,第二个题中女生比男生少,第三个题中女生比男生多。 小结:这三种题目看似不一样,实际上,都是已知一个数的几分之几是多少,求这个数。 3.已知两个量的和(差),其中一个量是另一个量的几分之几,求这两个量。 再来看看这道题,还有补充其他条件和问题的吗? (1)补充男女生人数的和。 上面这种方法特别好!我补充的也是男女生人数的和,但列的方程不一样。 对比这两种做法,使学生明白,列方程解决问题的时候,可以根据题目的特点设未知数。 份数的方法: (2)补充男女生人数的差。 学习时,我们就要学以致用。不同方法间还可以做到互相检验。 (3)对比两个题目,寻找相同点和不同点。 我们来回顾一下,这两道题有什么相同点,又有什么不同点呢? 不同点:第一个题给的是男女生人数的和,第二个题给的是男女人数的差。 相同点:女生人数是男生人数的。 这种题就是给了两个量的和或差,其中一个量是另一个量的几分之几,求这两个量。像这样的题都可以用方程解答。 三、巩固应用,深化理解 (一)看图列方程 第一题的方程是x+x=28 或(1+)x=28。 第二题的方程是x+x=330,(1+)x=330。 (二)修路问题 甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发,几小时后相遇? 学生讨论后明确:在解决问题的过程中,如果题目没有给出明确的总量,我们就都可以把它看成单位“1”。 四、全课总结 回顾今天的学习过程,说一说,你有什么收获? 生:在解决问题的过程中,分析题目的数量关系,找准单位“1”特别重要。 生:顺着题目的意思,根据分数乘法的意义,通过列方程解决单位“1”未知的问题非常好想! 生:无论是修路问题,还是相遇问题,都可以把题目中的总数量看成是“1”。 小结:你们通画图、对比等方法,不仅找到了题目之间的联系,还掌握了解决问题的方法。希望在以后的学习中,你们也能用到这些方法。 五、课后练习 1.完成数学书第42页第4题,第45页第4题。 2.用自己喜欢的方式梳理第三单元学习内容。
学习任务单
课程基本信息
学科 数学 年级 六年级 学期 秋季
课题 解决实际问题(第5课时)
教科书 书 名:义务教育教科书数学 出版社:人民教育出版社 出版日期:2022年8月
学生信息
姓名 学校 班级 学号
学习目标
1.进一步理解分数除法解决问题的几种类型,能根据题目的特点,选择合适的方法解决问题。 2.通过辨析比较,寻找知识之间的内在联系,进一步体会方程思想在数学中的应用,在解决问题的过程中建立数学模型,提高学生解决问题的能力。 3.感受数学与生活的联系,体会探究数学的乐趣。
课前学习任务
课上学习任务
【学习任务一】 补充合适的条件和问题,并尝试解答。 ,女生人数是男生人数的。 ? 【学习任务二】 【学习任务三】 甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发,几小时后相遇?
推荐的学习资源
课后练习
课程基本信息
学科 数学 年级 六年级 学期 秋季
课题 解决实际问题(第5课时)
教科书 书 名:义务教育教科书数学 出版社:人民教育出版社 出版日期:2022年8月
学生信息
姓名 学校 班级 学号
课后练习题目
1.数学书第42页第4题。 2.数学书第45页第4题。 3.用自己喜欢的方式梳理第三单元知识点、学习方法和学习经验等内容。
课后练习答案
参考答案: 1.正桥长度+引桥长度=1670 解:设这座大桥的正桥长x米,则引桥长x米。 x+x=1670 x=1670 x=1156 引桥:1670-1156=514(m) 答:这座大桥的正桥长1156m,则引桥长514m。 2.解法一:猎豹的速度×(1-)=狮子的速度 解:设猎豹奔跑时的最高时速为x千米/时。 (1-)x =60 x =60 x =110 答:猎豹奔跑时的最高时速为110千米/时。 解法二:猎豹的速度 - 猎豹速度× =狮子的速度 解:设猎豹奔跑时的最高时速为x千米/时。 x- x =60 x =60 x =110 答:猎豹奔跑时的最高时速为110千米/时。
课程基本信息
学科 数学 年级 六年级 学期 秋季
课题 解决实际问题(第5课时)
教科书 书 名:义务教育教科书数学 出版社:人民教育出版社 出版日期:2022年8月
教学目标
1.进一步理解分数除法解决问题的几种类型,能根据题目的特点,选择合适的方法解决问题。 2.通过辨析比较,寻找知识之间的内在联系,进一步体会方程思想在数学中的应用,在解决问题的过程中建立数学模型,提高学生解决问题的能力。 3.感受数学与生活的联系,体会探究数学的乐趣。
教学内容
教学重点: 沟通知识间的联系,体会方程思想的优势,建立数学模型。 教学难点: 体会方程思想的优势,建立数学模型。
教学过程
一、谈话引入 在前几节课的学习中,同学们利用方程解决了一些有关分数除法的实际问题,今天我们来上一节练习课。 二、学习交流中,深入理解知识 (一)分析关键信息 1.出示信息:女生人数是男生人数的。 从这句话中,你能分析出什么信息? 2.学生分析信息。 如:男生人数是单位“1”,把男生人数平均分成5份,女生人数是这样的3份。男生人数比女生人数多2份,男女生人数一共可以有8份;女生人数是所有人数的,男生人数是所有人数的 等等。 (二)补充条件,形成实际问题 1.学生讨论可以补充什么条件。 如果让同学们补充一个条件,把它变成学过的数学问题,想一想,可以补充什么条件? 学生思考,说一说可以补充什么条件。 比如:补充男生或女生的人数、男生和女生的总人数、男生和女生的人数差。在补充条件的过程中,引导学生观察数据的特点,选择合适的数据。 2.学生补充条件和问题,尝试解答。 听了前面几位同学的发言,相信大家都有了自己的想法。请你也补充上合适的条件和问题,并尝试解答。 (三)对比、辨析中,加深对知识的理解 1.已知单位“1”的数量,求单位“1”的几分之几是多少。 通过补充条件,把这道题变成了用分数乘法解决的实际问题。 2.已知单位“1”的几分之几是多少,求单位“1”的数量。 (1)已知男生的是多少,求男生人数。 (2)已知男生的(1- )是多少,求男生人数。 女生是男生的,还可以理解成女生比男生少,所以可以得到: 通过改变题目,我们得到了:已知男生的(1-)是多少,求男生人数。学习中,我们要善于寻找知识间的联系,让知识融会贯通! (3)已知男生的(1+ )是多少,求男生人数。 前两道题中,男生人数都是单位“1”,已知男生人数的和(1-)是多少,然后求男生人数。于是就想到了下面的题目。 (4)对比三个题目,寻找相同点和不同点。 这三道题放在一起,看一看,它们有什么相同点,又有什么不同点? 相同点:单位“1”都是男生人数,都求男生有多少人,都可以列方程解答的。 不同点:第一个题中女生是男生的,第二个题中女生比男生少,第三个题中女生比男生多。 小结:这三种题目看似不一样,实际上,都是已知一个数的几分之几是多少,求这个数。 3.已知两个量的和(差),其中一个量是另一个量的几分之几,求这两个量。 再来看看这道题,还有补充其他条件和问题的吗? (1)补充男女生人数的和。 上面这种方法特别好!我补充的也是男女生人数的和,但列的方程不一样。 对比这两种做法,使学生明白,列方程解决问题的时候,可以根据题目的特点设未知数。 份数的方法: (2)补充男女生人数的差。 学习时,我们就要学以致用。不同方法间还可以做到互相检验。 (3)对比两个题目,寻找相同点和不同点。 我们来回顾一下,这两道题有什么相同点,又有什么不同点呢? 不同点:第一个题给的是男女生人数的和,第二个题给的是男女人数的差。 相同点:女生人数是男生人数的。 这种题就是给了两个量的和或差,其中一个量是另一个量的几分之几,求这两个量。像这样的题都可以用方程解答。 三、巩固应用,深化理解 (一)看图列方程 第一题的方程是x+x=28 或(1+)x=28。 第二题的方程是x+x=330,(1+)x=330。 (二)修路问题 甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发,几小时后相遇? 学生讨论后明确:在解决问题的过程中,如果题目没有给出明确的总量,我们就都可以把它看成单位“1”。 四、全课总结 回顾今天的学习过程,说一说,你有什么收获? 生:在解决问题的过程中,分析题目的数量关系,找准单位“1”特别重要。 生:顺着题目的意思,根据分数乘法的意义,通过列方程解决单位“1”未知的问题非常好想! 生:无论是修路问题,还是相遇问题,都可以把题目中的总数量看成是“1”。 小结:你们通画图、对比等方法,不仅找到了题目之间的联系,还掌握了解决问题的方法。希望在以后的学习中,你们也能用到这些方法。 五、课后练习 1.完成数学书第42页第4题,第45页第4题。 2.用自己喜欢的方式梳理第三单元学习内容。
学习任务单
课程基本信息
学科 数学 年级 六年级 学期 秋季
课题 解决实际问题(第5课时)
教科书 书 名:义务教育教科书数学 出版社:人民教育出版社 出版日期:2022年8月
学生信息
姓名 学校 班级 学号
学习目标
1.进一步理解分数除法解决问题的几种类型,能根据题目的特点,选择合适的方法解决问题。 2.通过辨析比较,寻找知识之间的内在联系,进一步体会方程思想在数学中的应用,在解决问题的过程中建立数学模型,提高学生解决问题的能力。 3.感受数学与生活的联系,体会探究数学的乐趣。
课前学习任务
课上学习任务
【学习任务一】 补充合适的条件和问题,并尝试解答。 ,女生人数是男生人数的。 ? 【学习任务二】 【学习任务三】 甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发,几小时后相遇?
推荐的学习资源
课后练习
课程基本信息
学科 数学 年级 六年级 学期 秋季
课题 解决实际问题(第5课时)
教科书 书 名:义务教育教科书数学 出版社:人民教育出版社 出版日期:2022年8月
学生信息
姓名 学校 班级 学号
课后练习题目
1.数学书第42页第4题。 2.数学书第45页第4题。 3.用自己喜欢的方式梳理第三单元知识点、学习方法和学习经验等内容。
课后练习答案
参考答案: 1.正桥长度+引桥长度=1670 解:设这座大桥的正桥长x米,则引桥长x米。 x+x=1670 x=1670 x=1156 引桥:1670-1156=514(m) 答:这座大桥的正桥长1156m,则引桥长514m。 2.解法一:猎豹的速度×(1-)=狮子的速度 解:设猎豹奔跑时的最高时速为x千米/时。 (1-)x =60 x =60 x =110 答:猎豹奔跑时的最高时速为110千米/时。 解法二:猎豹的速度 - 猎豹速度× =狮子的速度 解:设猎豹奔跑时的最高时速为x千米/时。 x- x =60 x =60 x =110 答:猎豹奔跑时的最高时速为110千米/时。
