菱形、矩形、正方形(2,3,4)课时
图片预览





文档简介
课件58张PPT。矩形、菱形、正方形主讲教师:周咏梅 我们生活中充满了几何图形,教室里的黑板,门窗,课桌的桌面,信封明信片等都是矩形、菱形或正方形的形状,而你是否了解这两种几何图形的性质呢?
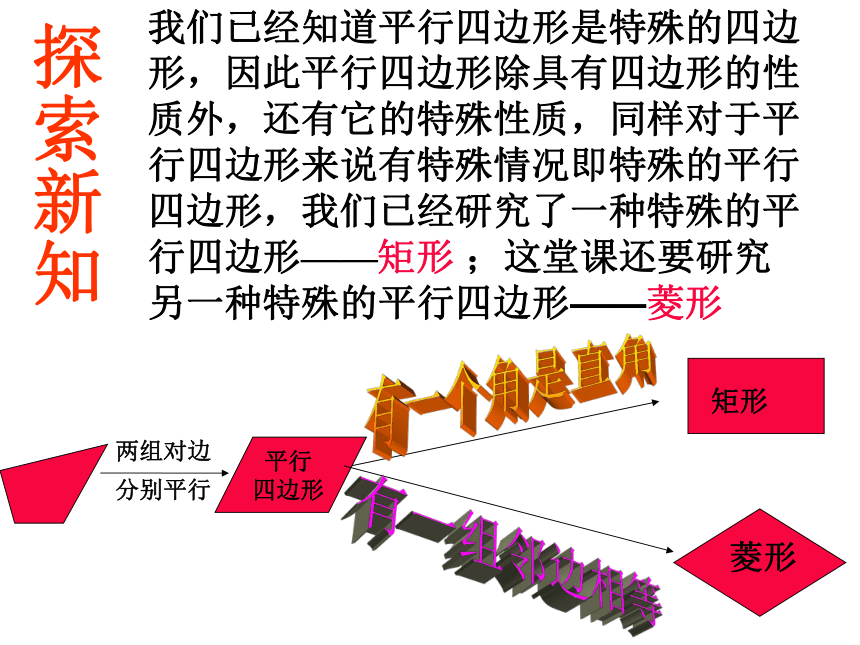
这一节我们继续研究特殊的四边形,我们先研究它们的性质,再研究它们的判定.菱形的性质两组对边
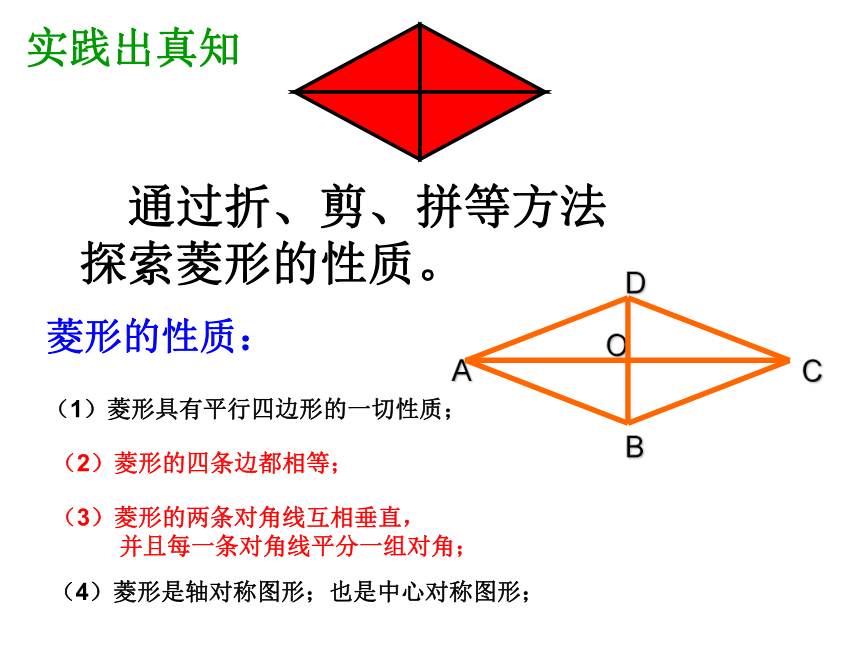
分别平行矩形我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,我们已经研究了一种特殊的平行四边形——矩形 ;这堂课还要研究另一种特殊的平行四边形——菱形有一个角是直角菱形有一组邻边相等探索新知有一组邻边相等的平行四边形叫做菱形;菱形的定义:AB=BC◇ABCD四边形ABCD是菱形 通过折、剪、拼等方法探索菱形的性质。实践出真知菱形的性质:(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直,
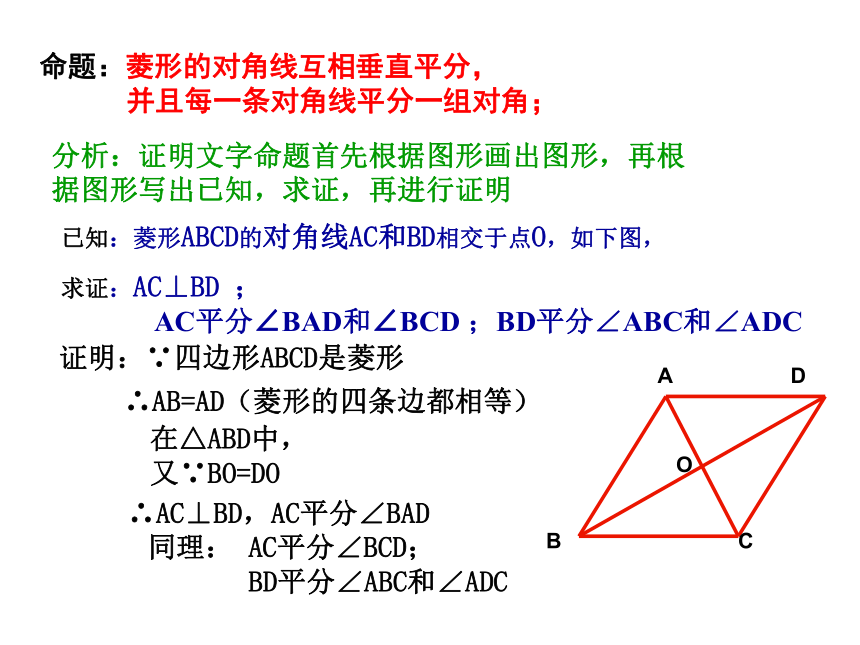
并且每一条对角线平分一组对角;(4)菱形是轴对称图形;也是中心对称图形;已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形在△ABD中,
又∵BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
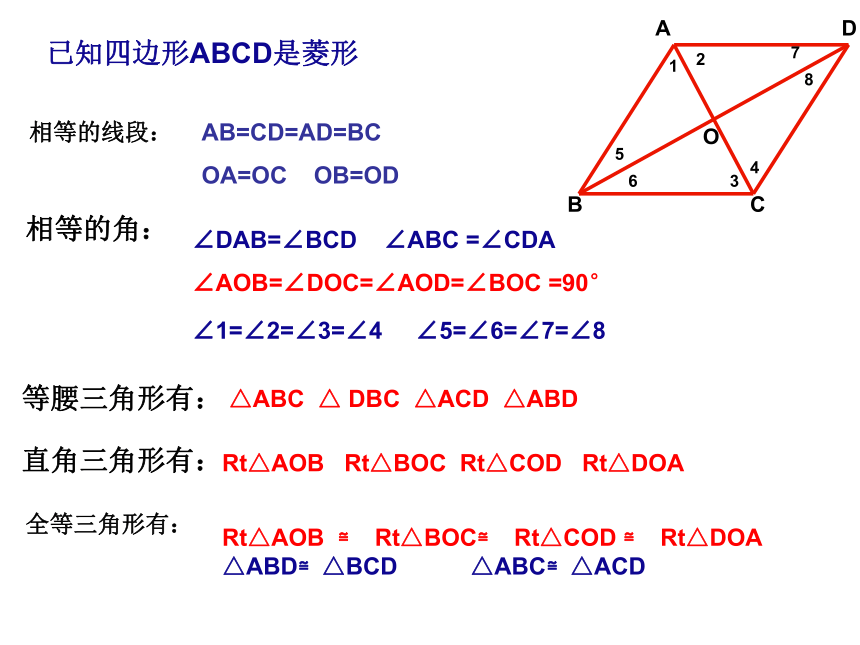
并且每一条对角线平分一组对角;分析:证明文字命题首先根据图形画出图形,再根据图形写出已知,求证,再进行证明相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678【菱形的面积公式】OES菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 菱形的面积=底×高=对角线乘积的一半1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.3cm60度例题教学分析:这两题是菱形性质的简单应用4.已知:菱形ABCD中,对角线AC与BD相交于点O,且 AC=12,BD=16,则菱形ABCD的面积为 ,边长为 ,周长为 。3.在菱形ABCD中,∠BAD=2∠B,则∠B= , △ABC是 三角形,∠ABD的度数为_____ 。等边30 °96104060 °5.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
解:∵四边形ABCD是菱形,
∴AB=CD(菱形的定义)
AC平分∠BAD(菱形的每条对角线平分一组对角)
∵∠BAC=30°
∴∠BAD=60°又∵OB=OD=3(平行四边形的对角线互相平分)
AC⊥BD(菱形的对角线互相垂直)
由勾股定理,得AO=
AC=2AO=∴ABD是等边三角形.
AB=BD=6例题教学注意解题过程的完整性,格式的规范性。6、如图,菱形ABCD的边长为4cm,∠BAD=1200。对角线AC、BD相交于点O,求这个菱形的对角线长和面积。。解:∵ ∠BAD=1200例题教学变式:已知菱形ABCD中,E是BC的中点,且AE⊥BC,AB=4.
求:⑴∠ABC的度数
⑵对角线AC的长
⑶菱形ABCD的面积解: ∵菱形ABCD
∴ AB=BC
∵ E是中点, AE⊥BC
∴AF是线段BC的垂直平分线
∴AB=AC
∴ △ BAC是等边三角形
∴∠ABC=600
余下部分与上题相同矩形的判定想一想1.矩形是平行四边形吗?2.怎样的平行四边形是矩形?矩形的定义:有一个角是直角的平行四边形是矩形。你还有其它的判定方法吗?∠A=900四边形ABCD是矩形你知道如何判定一个平行四边形是矩形吗?有一个角是直角的平行四边形是矩形矩形的判定矩形判定方法1有三个角是直角的四边形是矩形。矩形判定方法2对角线相等的平行四边形是矩形。矩形判定方法3证明:∵ ∠A=∠B=∠C=900
∴ ∠A+∠B=1800 , ∠B+∠C=1800
∴AD∥BC, AB∥CD
∴四边形ABCD是平行四边形。
∴四边形ABCD是矩形。ABDC定理1:有三个角是直角的四边形是矩形。已知:∠A=∠B=∠C=900
求证:四边形ABCD是矩形。证明:∵在 ABCD中,
AB=DC,AC=BD,BC=CB
∴△ABC≌△DCB
∴∠ABC=∠DCB
又∵AB∥DC
∴∠ABC+∠DCB=1800
∴∠ABC=∠DCB=900
∴ ABCD是矩形。
ABCD两条对角线相等的平行四边形是矩形。已知: ABCD中,AC=BD求证: ABCD是矩形。
练习:下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;XXXX 一位很有名望的木工师傅,招收了两名徒弟。一天,师傅有事外出,两徒弟就自已在家练习用两块四边形的废料各做了一扇矩形式的门,完事之后,两人都说对方的门不是矩形,而自已的是矩形。
甲的理由是:“我用角尺量我的门任意三个角,发现它们都是直角。所以我这个四边形门就是矩形”
乙的理由是:“我用直尺量这个门的两条对角线,发现它们的长度相等,所以我这个四边形门就是矩形”。
根据它们的对话,你能肯定谁的门一定是矩形。例2、谁正确?解:甲是正确的,因为有三个角是直角的四边形是矩形。
已不正确,因为对角线相等的四边形不一定是矩形,比如等腰梯形的对角线也相等。若要判断还要看四边形是否是平行四边形。例3:平行四边形ABCD,E是CD的中点, △ABE是等边三角形,
求证:四边形ABCD是矩形。证明:∵ △ABE是等边三角形
∴AE=BE
∵平行四边形ABCD
∴ AD=BC
又∵ E是CD的中点
∴DE=EC
∴△ADE≌△BC
∴ ∠ D =∠C
∴ ∠ D =∠C =1800∴ ∠ D =∠C =900
∴平行四边形ABCD是矩形例4 、已知:矩形的对角线ABCD的对角线AC、BD相交于点O,如E、F、G、H分别是AO、BO、CO、DO的中点.
求证:四边形EFGH是矩形.证明:∵矩形ABCD
∴AC=BD,
AO=CO=1/2AC
BO=DO=1/2BD
∴ AO=CO= BO=DO
又∵ EO=GO=1/2EG
FO=HO=1/2FH
∴EO=GO=FO=HO
∴四边形EFGH是矩形变式:已知:矩形的对角线ABCD的对角线AC、BD相交于点O,点E、F、G、H分别在OA、OB、OC、OD上,且AE=BF=CG=DH.
求证:四边形EFGH是矩形解:结论仍成立例4: 如果平行四边形四个内角的平分线能够围成一个四边形,那么这个四边形是矩形.变式:已知:AD∥BC,ME、NE、MF、NF分别为角平分线。
求证:(1)四边形ABCD为矩形(2)猜想EF和MN间的关系.分析:与上一题证明方法相同.思考:平行四边形ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P。
求证:四边形ABCD为矩形.证明:∵ PA⊥PC,PB⊥PD
∴ ∠APC= ∠BPD= 90°
又∵平行四边形ABCD
∴O是AC,BD的中点
∴PO=1/2BD, PO=1/2AC
∴ BD=AC
∴平行四边形ABCD是矩形菱形的判定 复习与回顾:1.菱形的定义:2.菱形的性质:有一组邻边相等的平行四边形叫做菱形。?
?
?对边平行
四边相等对角相等对角线互相平分、互相垂直且平分一组对角
菱形的判定1.菱形判定方法1:
有一组邻边相等的平行四边形叫做菱形。平行四边形符号语言:∵四边形ABCD是 平行四边形
AB=AD菱形的判定2.四条边相等的四边形是菱形吗?
已知:四边形ABCD中, AB=BC=CD=DA 求证:四边形ABCD是菱形。
菱形判定方法2:四条边相等的四边形是菱形∵AB=BC=CD=DA ∴四边形ABCD是菱形。
符号语言:已知:在 ABCD 中,对角线AC⊥BD
求证: ABCD是菱形。证明:∵四边形ABCD是平行四边形,
∴OB=OD又∵AC⊥BD∴AB=AD菱形判定方法3: 对角线互相垂直的平行四边形是菱形。符号语言:O练习巩固例1、选择: (一) 的平行四边形是菱形。( ) (二) 的四边形是菱形。 ( )1.一组邻边相等 2.四条边相等 3.对角线相等
4.对角线相等且互相平分 5.对角线互相垂直
6.对角线互相垂直且平分1526例题解析:例题解析:例3、已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F 求证:四边形AFCE是菱形。分析: (1)利用定义判定 (2) 由已知可知
OA=OC,EF⊥AC.(3)利用四边相等,你会吗? 分析:四边形AFCE是菱形AE=EC=CF=FAAE=ECAF=CFAE=AFEF 垂直平分AC∠1= ∠2∠1= ∠3∠2= ∠3AE∥FC四边形ABCD 是平行四边形AF=CF EF ⊥AC123 解:四边形CODP是菱形
∵ DP∥OC, DP=OC
∴ 四边形CODP是平行四边形 ∵四边形ABCD是矩形
∴CO=DO
∴四边形CODP是菱形 (2) PO与CD有怎样的关系?(2)PO与CD互相垂直且平分. 例5、 如图,两张等宽的纸条交重叠在一起,重叠的部分ABCD是菱形吗?为什么?EF分析: 此题只有利用面积进行解决.解: 过点A作AE⊥BC, AF⊥CD
∵两张等宽的纸条
∴AD∥BC, AB ∥ CD
∵ 四边形ABCD为平行四边形
又∵等宽
∴AE=AF
又∵S四边形ABCD=AE BC=AF CD
∴ BC=CD
∵ 四边形ABCD为菱形正方形的性质小结: 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。?正方形的性质= 正方形性质:
边: 对边平行
四边相等
角 :四个角都是直角对角线:相等
互相垂直平分
每条对角线平分一组对角。范例精讲求证: △ABO ≌ △BCO ≌ △CDO ≌△ADO 例1、求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。证明:∵正方形ABCD
∴AC=BD,
AO=CO=1/2AC
BO=DO=1/2BD
∴ AO=CO= BO=DO
又∵AC⊥ BD
∴ ∠AOB = ∠BOC=90 °∴ △ABO ≌ △BCO
同理可得:
△BCO ≌ △CDO ≌△ADO
已知:如图正方形ABCD对角线AC、BD,相交于点O。 例2.如图(3),正方形ABCD中,AC、BD相交于O, 分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
△ABM≌△BCNMN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 你能完成证明吗??? AB=BC,∠1=∠2=45 °条件够吗? 还需要的条件是 AM=BN你所要证明的两个三角形已经满足
了哪些条件?由正方形可以得到的条件有: 例2.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN下面大家自己完成证明例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等? △CMD≌△ADF变式:已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°证明:∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
例4.如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG 正方形的判定 你觉得什么样的四边形是正方形呢?正方形的判定1 定义法: 2、 对角线法: 两条对角线互相垂直平分且相等的四边形是正方形。有一组邻边相等的矩形是正方形。或有一个角是直角的菱形是正方形。3、矩形菱形法:既是矩形又是菱形的四边形是正方形。判断对错1. 四边相等的四边形是正方形 ( )
2.四角相等的四边形是正方形 ( )
3.对角线垂直的平行四边形是正方形( )
4.对角线互相垂直平分且相等的四 ( )
边形是正方形
5.四条边相等且有一个角是直角的四边形是正方形 ( )错错对对错例1.已知:如图,△ABC中.∠ABC=90°,BD是角平分线,DE⊥AB,DF⊥BC,垂足分别是E、F.求证:四边形DEBF是正方形.证明:∵ DF⊥BC,DE⊥AB,
∴ ∠DEB= ∠DFB=90°, 而∠ABC=90°, ∴四边形DEBF是矩形( ), ∵ BD平分∠ABC, DF⊥BC , DE⊥AB, ∴ DE= DF( ), ∴四边形DEBF是正方形( ). 矩形的判定定理角平分线的定理正方形的判定定理例2:在正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.四边形A`B`C`D`是正方形吗?为什么?123证明:∵正方形ABCD
∠A= ∠D=90°,
AB=BC=CA=AD
∵AA`=BB`=CC`=DD`
A`B=B`C=C`D=AD`
∴△AA`D` ≌△DD`C`
∴A`D` =D`C`
同理可得:A`B` =B`C`=D`C`
∵ ∠2= ∠3, ∠2+∠1= 90°
∴ ∠3+∠1= 90°
∴ ∠A`D`C` = 90°
∴四边形A`B`C`D`是正方形
有一组邻边相等有一个角是直角有一组邻边相等有一个角是直角平行四边形有一个角是直角有一组邻边相等
这一节我们继续研究特殊的四边形,我们先研究它们的性质,再研究它们的判定.菱形的性质两组对边
分别平行矩形我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,我们已经研究了一种特殊的平行四边形——矩形 ;这堂课还要研究另一种特殊的平行四边形——菱形有一个角是直角菱形有一组邻边相等探索新知有一组邻边相等的平行四边形叫做菱形;菱形的定义:AB=BC◇ABCD四边形ABCD是菱形 通过折、剪、拼等方法探索菱形的性质。实践出真知菱形的性质:(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;(4)菱形是轴对称图形;也是中心对称图形;已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形在△ABD中,
又∵BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
并且每一条对角线平分一组对角;分析:证明文字命题首先根据图形画出图形,再根据图形写出已知,求证,再进行证明相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
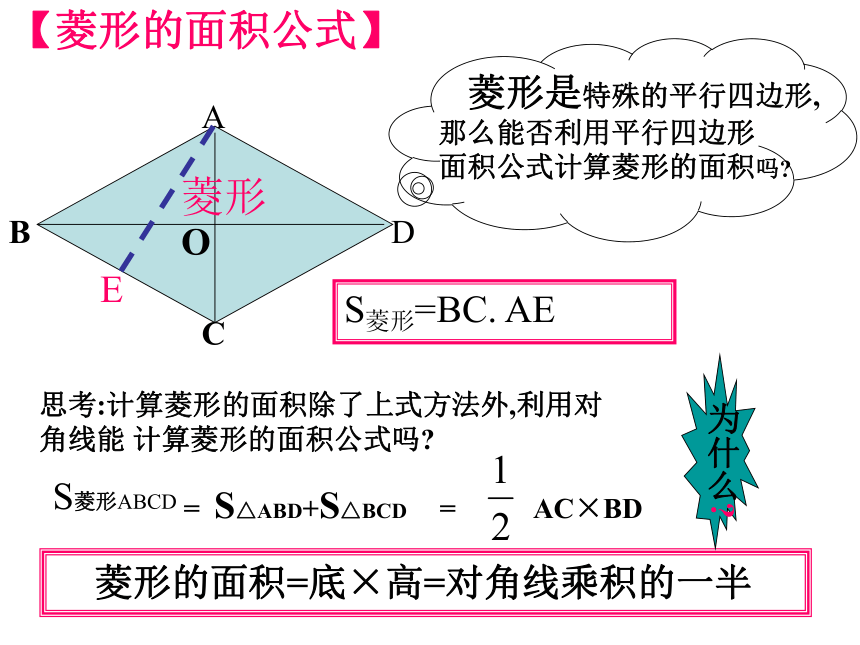
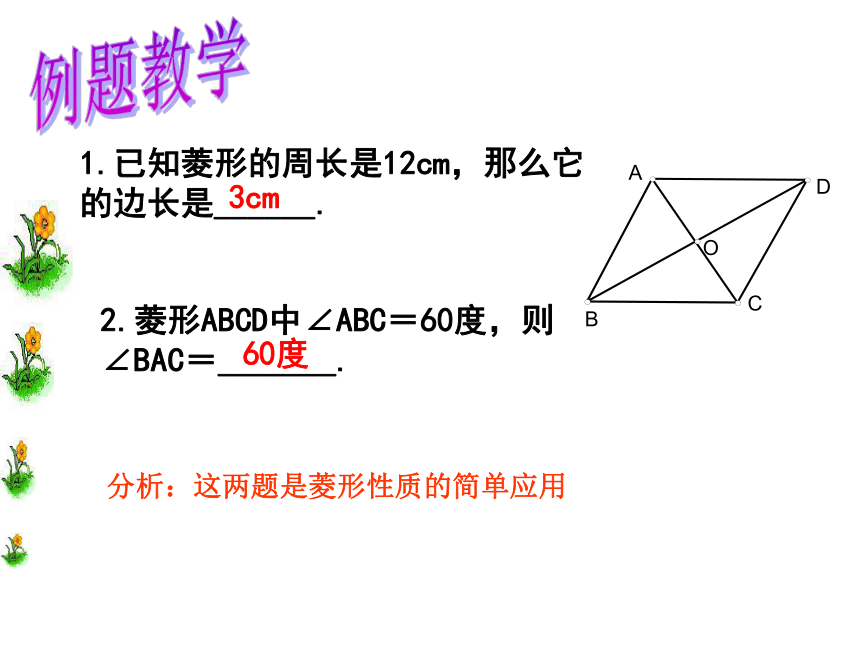
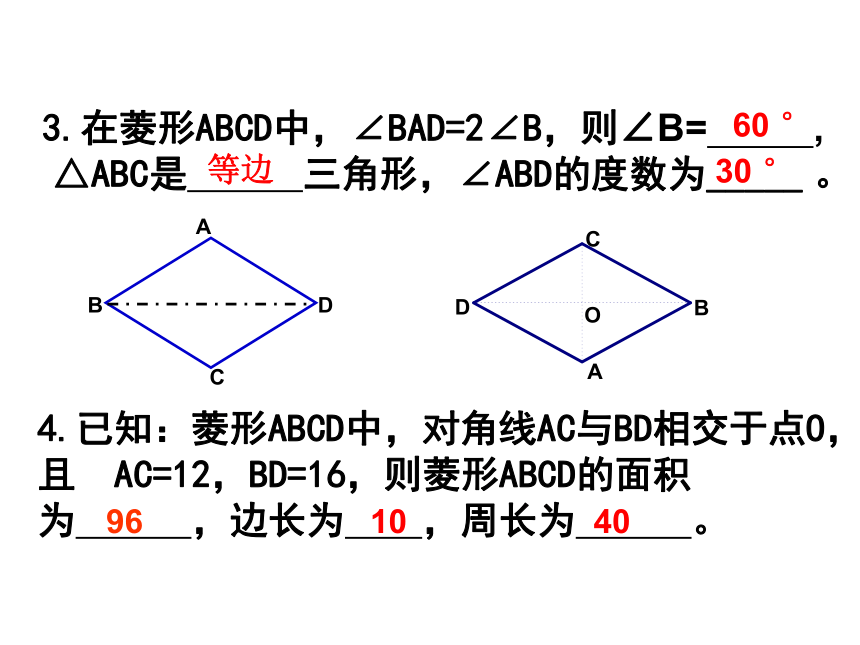
△ABD≌△BCD △ABC≌△ACDABCDO12345678【菱形的面积公式】OES菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 菱形的面积=底×高=对角线乘积的一半1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.3cm60度例题教学分析:这两题是菱形性质的简单应用4.已知:菱形ABCD中,对角线AC与BD相交于点O,且 AC=12,BD=16,则菱形ABCD的面积为 ,边长为 ,周长为 。3.在菱形ABCD中,∠BAD=2∠B,则∠B= , △ABC是 三角形,∠ABD的度数为_____ 。等边30 °96104060 °5.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
解:∵四边形ABCD是菱形,
∴AB=CD(菱形的定义)
AC平分∠BAD(菱形的每条对角线平分一组对角)
∵∠BAC=30°
∴∠BAD=60°又∵OB=OD=3(平行四边形的对角线互相平分)
AC⊥BD(菱形的对角线互相垂直)
由勾股定理,得AO=
AC=2AO=∴ABD是等边三角形.
AB=BD=6例题教学注意解题过程的完整性,格式的规范性。6、如图,菱形ABCD的边长为4cm,∠BAD=1200。对角线AC、BD相交于点O,求这个菱形的对角线长和面积。。解:∵ ∠BAD=1200例题教学变式:已知菱形ABCD中,E是BC的中点,且AE⊥BC,AB=4.
求:⑴∠ABC的度数
⑵对角线AC的长
⑶菱形ABCD的面积解: ∵菱形ABCD
∴ AB=BC
∵ E是中点, AE⊥BC
∴AF是线段BC的垂直平分线
∴AB=AC
∴ △ BAC是等边三角形
∴∠ABC=600
余下部分与上题相同矩形的判定想一想1.矩形是平行四边形吗?2.怎样的平行四边形是矩形?矩形的定义:有一个角是直角的平行四边形是矩形。你还有其它的判定方法吗?∠A=900四边形ABCD是矩形你知道如何判定一个平行四边形是矩形吗?有一个角是直角的平行四边形是矩形矩形的判定矩形判定方法1有三个角是直角的四边形是矩形。矩形判定方法2对角线相等的平行四边形是矩形。矩形判定方法3证明:∵ ∠A=∠B=∠C=900
∴ ∠A+∠B=1800 , ∠B+∠C=1800
∴AD∥BC, AB∥CD
∴四边形ABCD是平行四边形。
∴四边形ABCD是矩形。ABDC定理1:有三个角是直角的四边形是矩形。已知:∠A=∠B=∠C=900
求证:四边形ABCD是矩形。证明:∵在 ABCD中,
AB=DC,AC=BD,BC=CB
∴△ABC≌△DCB
∴∠ABC=∠DCB
又∵AB∥DC
∴∠ABC+∠DCB=1800
∴∠ABC=∠DCB=900
∴ ABCD是矩形。
ABCD两条对角线相等的平行四边形是矩形。已知: ABCD中,AC=BD求证: ABCD是矩形。
练习:下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;XXXX 一位很有名望的木工师傅,招收了两名徒弟。一天,师傅有事外出,两徒弟就自已在家练习用两块四边形的废料各做了一扇矩形式的门,完事之后,两人都说对方的门不是矩形,而自已的是矩形。
甲的理由是:“我用角尺量我的门任意三个角,发现它们都是直角。所以我这个四边形门就是矩形”
乙的理由是:“我用直尺量这个门的两条对角线,发现它们的长度相等,所以我这个四边形门就是矩形”。
根据它们的对话,你能肯定谁的门一定是矩形。例2、谁正确?解:甲是正确的,因为有三个角是直角的四边形是矩形。
已不正确,因为对角线相等的四边形不一定是矩形,比如等腰梯形的对角线也相等。若要判断还要看四边形是否是平行四边形。例3:平行四边形ABCD,E是CD的中点, △ABE是等边三角形,
求证:四边形ABCD是矩形。证明:∵ △ABE是等边三角形
∴AE=BE
∵平行四边形ABCD
∴ AD=BC
又∵ E是CD的中点
∴DE=EC
∴△ADE≌△BC
∴ ∠ D =∠C
∴ ∠ D =∠C =1800∴ ∠ D =∠C =900
∴平行四边形ABCD是矩形例4 、已知:矩形的对角线ABCD的对角线AC、BD相交于点O,如E、F、G、H分别是AO、BO、CO、DO的中点.
求证:四边形EFGH是矩形.证明:∵矩形ABCD
∴AC=BD,
AO=CO=1/2AC
BO=DO=1/2BD
∴ AO=CO= BO=DO
又∵ EO=GO=1/2EG
FO=HO=1/2FH
∴EO=GO=FO=HO
∴四边形EFGH是矩形变式:已知:矩形的对角线ABCD的对角线AC、BD相交于点O,点E、F、G、H分别在OA、OB、OC、OD上,且AE=BF=CG=DH.
求证:四边形EFGH是矩形解:结论仍成立例4: 如果平行四边形四个内角的平分线能够围成一个四边形,那么这个四边形是矩形.变式:已知:AD∥BC,ME、NE、MF、NF分别为角平分线。
求证:(1)四边形ABCD为矩形(2)猜想EF和MN间的关系.分析:与上一题证明方法相同.思考:平行四边形ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P。
求证:四边形ABCD为矩形.证明:∵ PA⊥PC,PB⊥PD
∴ ∠APC= ∠BPD= 90°
又∵平行四边形ABCD
∴O是AC,BD的中点
∴PO=1/2BD, PO=1/2AC
∴ BD=AC
∴平行四边形ABCD是矩形菱形的判定 复习与回顾:1.菱形的定义:2.菱形的性质:有一组邻边相等的平行四边形叫做菱形。?
?
?对边平行
四边相等对角相等对角线互相平分、互相垂直且平分一组对角
菱形的判定1.菱形判定方法1:
有一组邻边相等的平行四边形叫做菱形。平行四边形符号语言:∵四边形ABCD是 平行四边形
AB=AD菱形的判定2.四条边相等的四边形是菱形吗?
已知:四边形ABCD中, AB=BC=CD=DA 求证:四边形ABCD是菱形。
菱形判定方法2:四条边相等的四边形是菱形∵AB=BC=CD=DA ∴四边形ABCD是菱形。
符号语言:已知:在 ABCD 中,对角线AC⊥BD
求证: ABCD是菱形。证明:∵四边形ABCD是平行四边形,
∴OB=OD又∵AC⊥BD∴AB=AD菱形判定方法3: 对角线互相垂直的平行四边形是菱形。符号语言:O练习巩固例1、选择: (一) 的平行四边形是菱形。( ) (二) 的四边形是菱形。 ( )1.一组邻边相等 2.四条边相等 3.对角线相等
4.对角线相等且互相平分 5.对角线互相垂直
6.对角线互相垂直且平分1526例题解析:例题解析:例3、已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F 求证:四边形AFCE是菱形。分析: (1)利用定义判定 (2) 由已知可知
OA=OC,EF⊥AC.(3)利用四边相等,你会吗? 分析:四边形AFCE是菱形AE=EC=CF=FAAE=ECAF=CFAE=AFEF 垂直平分AC∠1= ∠2∠1= ∠3∠2= ∠3AE∥FC四边形ABCD 是平行四边形AF=CF EF ⊥AC123 解:四边形CODP是菱形
∵ DP∥OC, DP=OC
∴ 四边形CODP是平行四边形 ∵四边形ABCD是矩形
∴CO=DO
∴四边形CODP是菱形 (2) PO与CD有怎样的关系?(2)PO与CD互相垂直且平分. 例5、 如图,两张等宽的纸条交重叠在一起,重叠的部分ABCD是菱形吗?为什么?EF分析: 此题只有利用面积进行解决.解: 过点A作AE⊥BC, AF⊥CD
∵两张等宽的纸条
∴AD∥BC, AB ∥ CD
∵ 四边形ABCD为平行四边形
又∵等宽
∴AE=AF
又∵S四边形ABCD=AE BC=AF CD
∴ BC=CD
∵ 四边形ABCD为菱形正方形的性质小结: 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。?正方形的性质= 正方形性质:
边: 对边平行
四边相等
角 :四个角都是直角对角线:相等
互相垂直平分
每条对角线平分一组对角。范例精讲求证: △ABO ≌ △BCO ≌ △CDO ≌△ADO 例1、求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。证明:∵正方形ABCD
∴AC=BD,
AO=CO=1/2AC
BO=DO=1/2BD
∴ AO=CO= BO=DO
又∵AC⊥ BD
∴ ∠AOB = ∠BOC=90 °∴ △ABO ≌ △BCO
同理可得:
△BCO ≌ △CDO ≌△ADO
已知:如图正方形ABCD对角线AC、BD,相交于点O。 例2.如图(3),正方形ABCD中,AC、BD相交于O, 分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
△ABM≌△BCNMN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 你能完成证明吗??? AB=BC,∠1=∠2=45 °条件够吗? 还需要的条件是 AM=BN你所要证明的两个三角形已经满足
了哪些条件?由正方形可以得到的条件有: 例2.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN下面大家自己完成证明例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等? △CMD≌△ADF变式:已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°证明:∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
例4.如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG 正方形的判定 你觉得什么样的四边形是正方形呢?正方形的判定1 定义法: 2、 对角线法: 两条对角线互相垂直平分且相等的四边形是正方形。有一组邻边相等的矩形是正方形。或有一个角是直角的菱形是正方形。3、矩形菱形法:既是矩形又是菱形的四边形是正方形。判断对错1. 四边相等的四边形是正方形 ( )
2.四角相等的四边形是正方形 ( )
3.对角线垂直的平行四边形是正方形( )
4.对角线互相垂直平分且相等的四 ( )
边形是正方形
5.四条边相等且有一个角是直角的四边形是正方形 ( )错错对对错例1.已知:如图,△ABC中.∠ABC=90°,BD是角平分线,DE⊥AB,DF⊥BC,垂足分别是E、F.求证:四边形DEBF是正方形.证明:∵ DF⊥BC,DE⊥AB,
∴ ∠DEB= ∠DFB=90°, 而∠ABC=90°, ∴四边形DEBF是矩形( ), ∵ BD平分∠ABC, DF⊥BC , DE⊥AB, ∴ DE= DF( ), ∴四边形DEBF是正方形( ). 矩形的判定定理角平分线的定理正方形的判定定理例2:在正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.四边形A`B`C`D`是正方形吗?为什么?123证明:∵正方形ABCD
∠A= ∠D=90°,
AB=BC=CA=AD
∵AA`=BB`=CC`=DD`
A`B=B`C=C`D=AD`
∴△AA`D` ≌△DD`C`
∴A`D` =D`C`
同理可得:A`B` =B`C`=D`C`
∵ ∠2= ∠3, ∠2+∠1= 90°
∴ ∠3+∠1= 90°
∴ ∠A`D`C` = 90°
∴四边形A`B`C`D`是正方形
有一组邻边相等有一个角是直角有一组邻边相等有一个角是直角平行四边形有一个角是直角有一组邻边相等
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
