辽宁省葫芦岛市长江卫生中等职业技术学校2023-2024学年高二上学期期初数学试题(普高班)(含解析)
文档属性
| 名称 | 辽宁省葫芦岛市长江卫生中等职业技术学校2023-2024学年高二上学期期初数学试题(普高班)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 234.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 23:35:27 | ||
图片预览




文档简介
2023-2024高二期初考试
数学试卷(普高班)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1.已知a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( )
A.a∥c,b∥c B.a∥b,a⊥c
C.a∥c,a⊥b D.以上都不对
2.若直线过坐标平面内两点(1,2),(4,2+),则此直线的倾斜角是( )
A.30° B.45° C.60° D.90°
3.如果直线ax+2y+2=0与直线3x-y-2=0平行,那么a等于( )
A.-3 B.-6 C.- D.
4.两个不重合的平面α与平面ABC,若平面α的法向量为n=(2,-3,1),=(1,0,-2),=(1,1,1),则( )
A.平面α∥平面ABC B.平面α⊥平面ABC
C.平面α、平面ABC相交但不垂直 D.以上均有可能
5.空间四边形ABCD,连接AC,BD.M,G分别是BC,CD的中点,则等于 ( )
A. B. C. D.
6.当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心, 为半径的圆的方程为( )
A.(x-1)2+(y+2)2=5 B.(x+1)2+(y+2)2=5
C.(x+1)2+(y-2)2=5 D.(x-1)2+(y-2)2=5
7.已知直线l:3x+4y+m=0(m>0)被圆C:++2x-2y-6=0截得的弦长是圆心C到直线l的距离的2倍,则m等于( )
A.6 B.8 C.11 D.9
8.已知0A. B. C. D.1
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.设向量a,b,c可构成空间一个基底,下列选项中正确的是( )
A.若a⊥b,b⊥c,则a⊥c
B.则a,b,c两两共面,但a,b,c不可能共面
C.对空间任一向量p,总存在有序实数组(x,y,z),使p=xa+yb+zc
D.则a+b,b+c,c+a一定能构成空间的一个基底
10.如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=4,AA1=3,以直线DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系,则( )
A.点B1的坐标为(4,5,3)
B.点C1关于点B对称的点为(5,8,-3)
C.点A关于直线BD1对称的点为(0,5,3)
D.点C关于平面ABB1A1对称的点为(8,5,0)
11.若直线mx+2ny-4=0始终平分圆x2+y2-4x-2y-4=0的周长,则mn的取值可能是( )
A. B.- C. D.2
12.设有一组圆Ck:(x-k+1)2+(y-3k)2=2k4(k∈N*).下列四个命题中是真命题的有( )
A.存在一条定直线与所有的圆均相切 B.存在一条定直线与所有的圆均相交
C.存在一条定直线与所有的圆均不相交 D.所有的圆均不经过原点
三、填空题:本题共4小题,每小题5分,共20分.
13.若经过点(m,3)和(2,m)的直线l与斜率为-4的直线互相垂直,则m的值是 .
14.若点P(5a+1,12a)在圆(x-1)2+y2=1的外部,则a的取值范围为 .
15.设PA⊥Rt△ABC所在的平面α,∠BAC=90°,PB,PC分别与α成45°和30°角,PA=2,则PA与BC的距离是 ;点P到BC的距离是 .
16.已知向量m=(a,b,0),n=(c,d,1),其中a2+b2=c2+d2=1,现有以下命题:
①向量n与z轴正方向的夹角恒为定值(即与c,d无关);
②m·n的最大值为;
③(m,n的夹角)的最大值为;
④若定义u×v=|u|·|v|sin,则|m×n|的最大值为.
其中正确的命题有 .(写出所有正确命题的序号)
解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知空间中三点A(2,0,-2),B(1,-1,-2),C(3,0,-4),设a=,b=.
(1)若|c|=3,且c∥,求向量c;
(2)已知向量ka+b与b互相垂直,求k的值;
(3)求△ABC的面积.
18.如图,在等腰梯形ABCD中,AB∥CD,边AB所在直线方程为2x-y-2=0,点C(2,0),|BC|=1,B为第一象限上的点.
(1)求点B坐标;
(2)求AB边上的高CE所在直线的方程;
(3)求直线AB与直线CD之间的距离.
19.已知圆C的方程可以表示为x2+y2-2x-4y+m=0,其中m∈R.
(1)若m=1,求圆C被直线x+y-1=0截得的弦长;
(2)若圆C与直线l:x+2y-4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m的值.
20.已知直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)和圆C:x2+y2-8x-6y+5=0.
(1)求证:直线l恒过一定点M;
(2)试求当m为何值时,直线l被圆C所截得的弦长最短;
(3)在(2)的前提下,直线l'是过点N(-1,-2)且与直线l平行的直线,求圆心在直线l'上,且与圆C相外切的动圆中半径最小的圆的标准方程.
21.如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
(1)求证:AB∥GH;
(2)求平面DGH与平面GHE的夹角的余弦值.
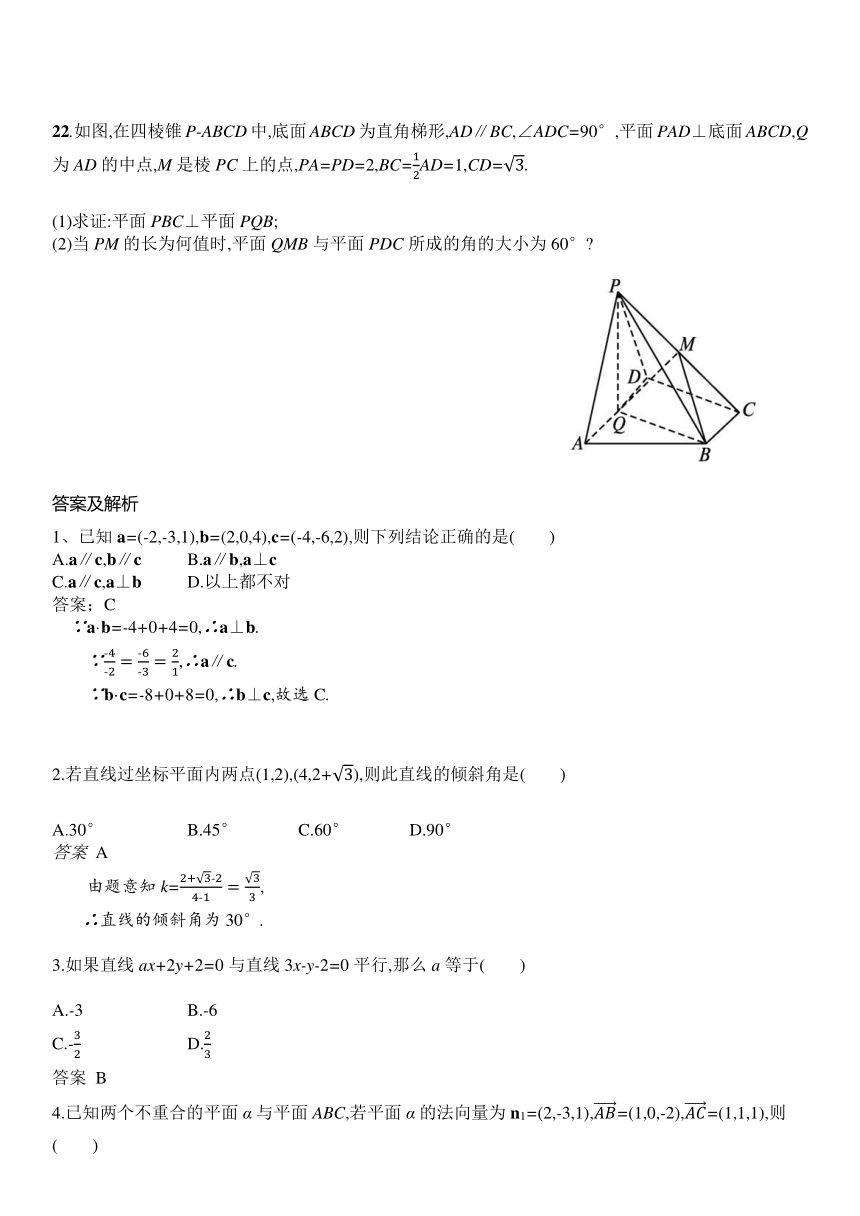
22.如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=AD=1,CD=.
(1)求证:平面PBC⊥平面PQB;
(2)当PM的长为何值时,平面QMB与平面PDC所成的角的大小为60°
答案及解析
1、已知a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( )
A.a∥c,b∥c B.a∥b,a⊥c
C.a∥c,a⊥b D.以上都不对
答案;C
∵a·b=-4+0+4=0,∴a⊥b.
∵,∴a∥c.
∵b·c=-8+0+8=0,∴b⊥c,故选C.
2.若直线过坐标平面内两点(1,2),(4,2+),则此直线的倾斜角是( )
A.30° B.45° C.60° D.90°
答案 A
由题意知k=,
∴直线的倾斜角为30°.
3.如果直线ax+2y+2=0与直线3x-y-2=0平行,那么a等于( )
A.-3 B.-6
C.- D.
答案 B
4.已知两个不重合的平面α与平面ABC,若平面α的法向量为n1=(2,-3,1),=(1,0,-2),=(1,1,1),则( )
A.平面α∥平面ABC
B.平面α⊥平面ABC
C.平面α、平面ABC相交但不垂直
D.以上均有可能
答案 A
由题意,计算n1·=2×1+(-3)×0+1×(-2)=0,得n1⊥,
计算n1·=2×1+(-3)×1+1×1=0,得n1⊥,所以n1⊥平面ABC,
所以平面α的法向量与平面ABC的法向量共线,
则平面α∥平面ABC.
5.如图所示,已知空间四边形ABCD,连接AC,BD.M,G分别是BC,CD的中点,则等于 ( )
A. B.
C. D.
答案C
∵M,G分别是BC,CD的中点,
∴.
∴.
6.当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心, 为半径的圆的方程为( )
A.(x-1)2+(y+2)2=5
B.(x+1)2+(y+2)2=5
C.(x+1)2+(y-2)2=5
D.(x-1)2+(y-2)2=5
答案C
[直线方程变为(x+1)a-x-y+1=0.
由得∴C(-1,2),∴所求圆的方程为(x+1)2+(y-2)2=5.]
7.已知直线l:3x+4y+m=0(m>0)被圆C:x2+y2+2x-2y-6=0截得的弦长是圆心C到直线l的距离的2倍,则m等于( )
A.6 B.8 C.11 D.9
答案D
圆C:x2+y2+2x-2y-6=0可化为(x+1)2+(y-1)2=8,圆心坐标为(-1,1),半径为2,
由题意可知,圆心到直线的距离d==2.
∵m>0,∴m=9.
8.已知0A. B. C. D.1
答案C
l1:k(x-2)-2y+8=0过定点(2,4),l2:k2(y-4)=4-2x也过定点(2,4),如图所示,点A(0,4-k),B(2k2+2,0),S=×2k2×4+(4-k+4)×2×=4k2-k+8.
当k=时,S取得最小值.
9.设向量a,b,c可构成空间一个基底,下列选项中正确的是( )
A.若a⊥b,b⊥c,则a⊥c
B.则a,b,c两两共面,但a,b,c不可能共面
C.对空间任一向量p,总存在有序实数组(x,y,z),使p=xa+yb+zc
D.则a+b,b+c,c+a一定能构成空间的一个基底
答案BCD
由a,b,c是空间一个基底,知:
在A中,若a⊥b,b⊥c,则a与c相交或平行,故A错误;
在B中,a,b,c两两共面,但a,b,c不可能共面,故B正确;
在C中,对空间任一向量p,总存在有序实数组(x,y,z),使p=xa+yb+zc,故C正确;
在D中,a+b,b+c,c+a一定能构成空间的一个基底,故D正确.
10.如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=4,AA1=3,以直线DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系,则( )
A.点B1的坐标为(4,5,3)
B.点C1关于点B对称的点为(5,8,-3)
C.点A关于直线BD1对称的点为(0,5,3)
D.点C关于平面ABB1A1对称的点为(8,5,0)
答案 ACD
由图形及其已知可得,点B1的坐标为(4,5,3),点C1(0,5,3)关于点B(4,5,0)对称的点为(8,5,-3),点A关于直线BD1对称的点为C1(0,5,3),点C(0,5,0)关于平面ABB1A1对称的点为(8,5,0).故A,C,D正确.
11.若直线mx+2ny-4=0始终平分圆x2+y2-4x-2y-4=0的周长,则mn的取值可能是( )
A. B.-
C. D.2
答案ABC
[可知直线mx+2ny-4=0过圆心(2,1),
有2m+2n-4=0,即n=2-m,则mn=m·(2-m)=-m2+2m=-(m-1)2+1≤1.]
12.设有一组圆Ck:(x-k+1)2+(y-3k)2=2k4(k∈N*).下列四个命题中是真命题的有( )
A.存在一条定直线与所有的圆均相切
B.存在一条定直线与所有的圆均相交
C.存在一条定直线与所有的圆均不相交
D.所有的圆均不经过原点
答案BD
根据题意得,圆心(k-1,3k),圆心在直线y=3(x+1)上,故存在直线y=3(x+1)与所有圆都相交,选项B正确;
考虑两圆的位置关系,
圆Ck:圆心(k-1,3k),半径为r=k2,
圆Ck+1:圆心(k-1+1,3(k+1)),
即(k,3k+3),半径为R=(k+1)2,
两圆的圆心距d=,两圆的半径之差R-r=(k+1)2-k2=2k+,任取k=1或2时,(R-r>d),Ck含于Ck+1之中,选项A错误;
若k取无穷大,则可以认为所有直线都与圆相交,选项C错误;
将(0,0)代入圆的方程,则有(-k+1)2+9k2=2k4,
即10k2-2k+1=2k4(k∈N*),
因为左边为奇数,右边为偶数,故不存在k使上式成立,即所有圆均不过原点,选项D正确.
13.若经过点(m,3)和(2,m)的直线l与斜率为-4的直线互相垂直,则m的值是 .
由题意可知kl=,又因为kl=,
所以,解得m=.
14.若点P(5a+1,12a)在圆(x-1)2+y2=1的外部,则a的取值范围为 .
答案a>或a<-
[∵P在圆外,∴(5a+1-1)2+(12a)2>1,169a2>1,a2>,∴|a|>,即a>或a<-.]
15.设PA⊥Rt△ABC所在的平面α,∠BAC=90°,PB,PC分别与α成45°和30°角,PA=2,则PA与BC的距离是 ;点P到BC的距离是 .
答案
作AD⊥BC于点D,
∵PA⊥面ABC,
∴PA⊥AD.∴AD是PA与BC的公垂线.
易得AB=2,AC=2,BC=4,AD=,连接PD,则PD⊥BC,P到BC的距离PD=.
16.已知向量m=(a,b,0),n=(c,d,1),其中a2+b2=c2+d2=1,现有以下命题:
①向量n与z轴正方向的夹角恒为定值(即与c,d无关);
②m·n的最大值为;
③(m,n的夹角)的最大值为;
④若定义u×v=|u|·|v|sin,则|m×n|的最大值为.
其中正确的命题有 .(写出所有正确命题的序号)
答案①③④
①取z轴的正方向单位向量a=(0,0,1),
则cos=,∴向量n与z轴正方向的夹角恒为定值,命题正确;
②m·n=ac+bd≤=1,
当且仅当a=c,b=d时取等号,因此m·n的最大值为1,命题错误;
③由②可得|m·n|≤1,∴-1≤m·n≤1,
∴cos=
=≥-=-,
∴的最大值是,命题正确;
④由③可知:-≤cos≤,
∴≤≤≤sin≤1,∴m×n=|m|×|n|×sin≤1××1=,命题正确.
综上可知,正确的命题序号是①③④.
17.已知空间中三点A(2,0,-2),B(1,-1,-2),C(3,0,-4),设a=,b=.
(1)若|c|=3,且c∥,求向量c;
(2)已知向量ka+b与b互相垂直,求k的值;
(3)求△ABC的面积.
(1)∵空间中三点A(2,0,-2),B(1,-1,-2),C(3,0,-4),设a=,b=,
∴=(3,0,-4)-(1,-1,-2)=(2,1,-2),
∵|c|=3,且c∥,
∴c=m=m(2,1,-2)=(2m,m,-2m),
∴|c|==3|m|=3,
∴m=±1,∴c=(2,1,-2)或c=(-2,-1,2).
(2)由题得a=(-1,-1,0),b=(1,0,-2),
∴ka+b=k(-1,-1,0)+(1,0,-2)=(1-k,-k,-2),
∵向量ka+b与b互相垂直,∴(ka+b)·b=1-k+4=0,解得k=5.∴k的值是5.
(3)=(-1,-1,0),=(1,0,-2),=(2,1,-2),
cos<>==-,sin<>=,
∴S△ABC=×||×||×sin<>=.
18.如图,在等腰梯形ABCD中,AB∥CD,边AB所在直线方程为2x-y-2=0,点C(2,0),|BC|=1,B为第一象限上的点.
(1)求点B坐标;
(2)求AB边上的高CE所在直线的方程;
(3)求直线AB与直线CD之间的距离.
(1)设B(a,2a-2),∵C(2,0),|BC|=1,
∴=1,解得a=1或a=.
∵B为第一象限上的点,∴2a-2>0,即a>1.
∴a=,则B.
(2)∵边AB所在直线方程为2x-y-2=0,
∴kCE=-=-.
又∵CE经过点C(2,0),∴AB边上的高CE所在直线的方程为y=-x+1,即x+2y-2=0.
(3)∵AB∥CD,∴kCD=kAB=2.
∵点C(2,0),
∴直线CD的方程为y=2(x-2),
即2x-y-4=0.
又AB所在直线方程为2x-y-2=0,
则直线AB与直线CD之间的距离d=.
19.已知圆C的方程可以表示为x2+y2-2x-4y+m=0,其中m∈R.
(1)若m=1,求圆C被直线x+y-1=0截得的弦长;
(2)若圆C与直线l:x+2y-4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m的值.
(1)m=1,配方得(x-1)2+(y-2)2=4,圆心到直线的距离为,
所以圆C被直线x+y-1=0截得的弦长为2=2.
(2)设M(x1,y1),N(x2,y2),
直线代入圆的方程得5x2-8x+4(m-4)=0,
所以x1+x2=,x1x2=.
因为OM⊥ON,所以x1x2+y1y2=0,
所以+4=0,
所以m=,此时Δ>0.
20.已知直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)和圆C:x2+y2-8x-6y+5=0.
(1)求证:直线l恒过一定点M;
(2)试求当m为何值时,直线l被圆C所截得的弦长最短;
(3)在(2)的前提下,直线l'是过点N(-1,-2)且与直线l平行的直线,求圆心在直线l'上,且与圆C相外切的动圆中半径最小的圆的标准方程.
(1)由直线l:(2m+1)x+(m+1)y-7m-4=0,得m(2x+y-7)+x+y-4=0,
联立解得
∴直线l恒过一定点M(3,1).
(2)要使直线l被圆C所截得的弦长最短,则l⊥CM,
化圆C:x2+y2-8x-6y+5=0为(x-4)2+(y-3)2=20,可得C(4,3),则kCM==2,
∴-=-,解得m=-.
(3)由(2)得,直线l':y+2=-(x+1),即x+2y+5=0.
如图,过C与直线x+2y+5=0垂直的直线方程为y-3=2(x-4),即2x-y-5=0.
联立
解得
而C到直线x+2y+5=0的距离d==3,
∴所求圆的半径为3-2.
故圆心在直线l'上,且与圆C相外切的动圆中半径最小的圆的标准方程为(x-1)2+(y+3)2=5.
21.如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
(1)求证:AB∥GH;
(2)求平面DGH与平面GHE的夹角的余弦值.
(1)因为D,C,E,F分别是AQ,BQ,AP,BP的中点,所以EF∥AB,DC∥AB.所以EF∥DC.
又EF 平面PCD,DC 平面PCD,
所以EF∥平面PCD.
又EF 平面EFQ,平面EFQ∩平面PCD=GH,
所以EF∥GH.又EF∥AB,所以AB∥GH.
(2)在△ABQ中,AQ=2BD,AD=DQ,
所以∠ABQ=90°.
又PB⊥平面ABQ,所以BA,BQ,BP两两垂直.
以B为坐标原点,分别以BA,BQ,BP所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
设BA=BQ=BP=2,
则E(1,0,1),F(0,0,1),Q(0,2,0),D(1,1,0),C(0,1,0),P(0,0,2).
所以=(-1,2,-1),=(0,2,-1),
=(-1,-1,2),=(0,-1,2).
设平面EFQ的一个法向量为m=(x1,y1,z1),
由m·=0,m·=0,
得取y1=1,得m=(0,1,2).
设平面PDC的一个法向量为n=(x2,y2,z2),
由n·=0,n·=0,
得取z2=1,得n=(0,2,1).
设平面DGH与平面GHE的夹角为θ,
则cosθ=|cos|=.
22.(12分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=AD=1,CD=.
(1)求证:平面PBC⊥平面PQB;
(2)当PM的长为何值时,平面QMB与平面PDC所成的角的大小为60°
(1)∵AD∥BC,Q为AD的中点,BC=AD,
∴BC∥QD,BC=QD,
∴四边形BCDQ为平行四边形,∴BQ∥CD.
∵∠ADC=90°,∴BC⊥BQ.
∵PA=PD,AQ=QD,∴PQ⊥AD.
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PQ⊥平面ABCD,∴PQ⊥BC.
又∵PQ∩BQ=Q,∴BC⊥平面PQB.
∵BC 平面PBC,∴平面PBC⊥平面PQB.
(2)由(1)可知PQ⊥平面ABCD.如图,以Q为原点,分别以QA,QB,QP所在直线为x轴,y轴,z轴,建立空间直角坐标系,则Q(0,0,0),D(-1,0,0),P(0,0,),B(0,,0),C(-1,,0),
∴=(0,,0),=(0,,0),=(1,0,),=(-1,,-),
PC=.
设=λ,则=(-λ,λ,-λ),且0≤λ≤1,得M(-λ,λ,λ),
∴=(-λ,λ,(1-λ)).
设平面MBQ的法向量为m=(x,y,z),则
令x=,则y=0,z=,∴平面MBQ的一个法向量为m=,0,.
设平面PDC的法向量为n=(x',y',z'),则
令x'=3,则y'=0,z'=-,∴平面PDC的一个法向量为n=(3,0,-).
∴平面QMB与平面PDC所成的锐二面角的大小为60°,
∴cos60°=,
∴λ=.∴PM=PC=.即当PM=时,平面QMB与平面PDC所成的角大小为60°.
数学试卷(普高班)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1.已知a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( )
A.a∥c,b∥c B.a∥b,a⊥c
C.a∥c,a⊥b D.以上都不对
2.若直线过坐标平面内两点(1,2),(4,2+),则此直线的倾斜角是( )
A.30° B.45° C.60° D.90°
3.如果直线ax+2y+2=0与直线3x-y-2=0平行,那么a等于( )
A.-3 B.-6 C.- D.
4.两个不重合的平面α与平面ABC,若平面α的法向量为n=(2,-3,1),=(1,0,-2),=(1,1,1),则( )
A.平面α∥平面ABC B.平面α⊥平面ABC
C.平面α、平面ABC相交但不垂直 D.以上均有可能
5.空间四边形ABCD,连接AC,BD.M,G分别是BC,CD的中点,则等于 ( )
A. B. C. D.
6.当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心, 为半径的圆的方程为( )
A.(x-1)2+(y+2)2=5 B.(x+1)2+(y+2)2=5
C.(x+1)2+(y-2)2=5 D.(x-1)2+(y-2)2=5
7.已知直线l:3x+4y+m=0(m>0)被圆C:++2x-2y-6=0截得的弦长是圆心C到直线l的距离的2倍,则m等于( )
A.6 B.8 C.11 D.9
8.已知0
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.设向量a,b,c可构成空间一个基底,下列选项中正确的是( )
A.若a⊥b,b⊥c,则a⊥c
B.则a,b,c两两共面,但a,b,c不可能共面
C.对空间任一向量p,总存在有序实数组(x,y,z),使p=xa+yb+zc
D.则a+b,b+c,c+a一定能构成空间的一个基底
10.如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=4,AA1=3,以直线DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系,则( )
A.点B1的坐标为(4,5,3)
B.点C1关于点B对称的点为(5,8,-3)
C.点A关于直线BD1对称的点为(0,5,3)
D.点C关于平面ABB1A1对称的点为(8,5,0)
11.若直线mx+2ny-4=0始终平分圆x2+y2-4x-2y-4=0的周长,则mn的取值可能是( )
A. B.- C. D.2
12.设有一组圆Ck:(x-k+1)2+(y-3k)2=2k4(k∈N*).下列四个命题中是真命题的有( )
A.存在一条定直线与所有的圆均相切 B.存在一条定直线与所有的圆均相交
C.存在一条定直线与所有的圆均不相交 D.所有的圆均不经过原点
三、填空题:本题共4小题,每小题5分,共20分.
13.若经过点(m,3)和(2,m)的直线l与斜率为-4的直线互相垂直,则m的值是 .
14.若点P(5a+1,12a)在圆(x-1)2+y2=1的外部,则a的取值范围为 .
15.设PA⊥Rt△ABC所在的平面α,∠BAC=90°,PB,PC分别与α成45°和30°角,PA=2,则PA与BC的距离是 ;点P到BC的距离是 .
16.已知向量m=(a,b,0),n=(c,d,1),其中a2+b2=c2+d2=1,现有以下命题:
①向量n与z轴正方向的夹角恒为定值(即与c,d无关);
②m·n的最大值为;
③
④若定义u×v=|u|·|v|sin
其中正确的命题有 .(写出所有正确命题的序号)
解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知空间中三点A(2,0,-2),B(1,-1,-2),C(3,0,-4),设a=,b=.
(1)若|c|=3,且c∥,求向量c;
(2)已知向量ka+b与b互相垂直,求k的值;
(3)求△ABC的面积.
18.如图,在等腰梯形ABCD中,AB∥CD,边AB所在直线方程为2x-y-2=0,点C(2,0),|BC|=1,B为第一象限上的点.
(1)求点B坐标;
(2)求AB边上的高CE所在直线的方程;
(3)求直线AB与直线CD之间的距离.
19.已知圆C的方程可以表示为x2+y2-2x-4y+m=0,其中m∈R.
(1)若m=1,求圆C被直线x+y-1=0截得的弦长;
(2)若圆C与直线l:x+2y-4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m的值.
20.已知直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)和圆C:x2+y2-8x-6y+5=0.
(1)求证:直线l恒过一定点M;
(2)试求当m为何值时,直线l被圆C所截得的弦长最短;
(3)在(2)的前提下,直线l'是过点N(-1,-2)且与直线l平行的直线,求圆心在直线l'上,且与圆C相外切的动圆中半径最小的圆的标准方程.
21.如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
(1)求证:AB∥GH;
(2)求平面DGH与平面GHE的夹角的余弦值.
22.如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=AD=1,CD=.
(1)求证:平面PBC⊥平面PQB;
(2)当PM的长为何值时,平面QMB与平面PDC所成的角的大小为60°
答案及解析
1、已知a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( )
A.a∥c,b∥c B.a∥b,a⊥c
C.a∥c,a⊥b D.以上都不对
答案;C
∵a·b=-4+0+4=0,∴a⊥b.
∵,∴a∥c.
∵b·c=-8+0+8=0,∴b⊥c,故选C.
2.若直线过坐标平面内两点(1,2),(4,2+),则此直线的倾斜角是( )
A.30° B.45° C.60° D.90°
答案 A
由题意知k=,
∴直线的倾斜角为30°.
3.如果直线ax+2y+2=0与直线3x-y-2=0平行,那么a等于( )
A.-3 B.-6
C.- D.
答案 B
4.已知两个不重合的平面α与平面ABC,若平面α的法向量为n1=(2,-3,1),=(1,0,-2),=(1,1,1),则( )
A.平面α∥平面ABC
B.平面α⊥平面ABC
C.平面α、平面ABC相交但不垂直
D.以上均有可能
答案 A
由题意,计算n1·=2×1+(-3)×0+1×(-2)=0,得n1⊥,
计算n1·=2×1+(-3)×1+1×1=0,得n1⊥,所以n1⊥平面ABC,
所以平面α的法向量与平面ABC的法向量共线,
则平面α∥平面ABC.
5.如图所示,已知空间四边形ABCD,连接AC,BD.M,G分别是BC,CD的中点,则等于 ( )
A. B.
C. D.
答案C
∵M,G分别是BC,CD的中点,
∴.
∴.
6.当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心, 为半径的圆的方程为( )
A.(x-1)2+(y+2)2=5
B.(x+1)2+(y+2)2=5
C.(x+1)2+(y-2)2=5
D.(x-1)2+(y-2)2=5
答案C
[直线方程变为(x+1)a-x-y+1=0.
由得∴C(-1,2),∴所求圆的方程为(x+1)2+(y-2)2=5.]
7.已知直线l:3x+4y+m=0(m>0)被圆C:x2+y2+2x-2y-6=0截得的弦长是圆心C到直线l的距离的2倍,则m等于( )
A.6 B.8 C.11 D.9
答案D
圆C:x2+y2+2x-2y-6=0可化为(x+1)2+(y-1)2=8,圆心坐标为(-1,1),半径为2,
由题意可知,圆心到直线的距离d==2.
∵m>0,∴m=9.
8.已知0
答案C
l1:k(x-2)-2y+8=0过定点(2,4),l2:k2(y-4)=4-2x也过定点(2,4),如图所示,点A(0,4-k),B(2k2+2,0),S=×2k2×4+(4-k+4)×2×=4k2-k+8.
当k=时,S取得最小值.
9.设向量a,b,c可构成空间一个基底,下列选项中正确的是( )
A.若a⊥b,b⊥c,则a⊥c
B.则a,b,c两两共面,但a,b,c不可能共面
C.对空间任一向量p,总存在有序实数组(x,y,z),使p=xa+yb+zc
D.则a+b,b+c,c+a一定能构成空间的一个基底
答案BCD
由a,b,c是空间一个基底,知:
在A中,若a⊥b,b⊥c,则a与c相交或平行,故A错误;
在B中,a,b,c两两共面,但a,b,c不可能共面,故B正确;
在C中,对空间任一向量p,总存在有序实数组(x,y,z),使p=xa+yb+zc,故C正确;
在D中,a+b,b+c,c+a一定能构成空间的一个基底,故D正确.
10.如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=4,AA1=3,以直线DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系,则( )
A.点B1的坐标为(4,5,3)
B.点C1关于点B对称的点为(5,8,-3)
C.点A关于直线BD1对称的点为(0,5,3)
D.点C关于平面ABB1A1对称的点为(8,5,0)
答案 ACD
由图形及其已知可得,点B1的坐标为(4,5,3),点C1(0,5,3)关于点B(4,5,0)对称的点为(8,5,-3),点A关于直线BD1对称的点为C1(0,5,3),点C(0,5,0)关于平面ABB1A1对称的点为(8,5,0).故A,C,D正确.
11.若直线mx+2ny-4=0始终平分圆x2+y2-4x-2y-4=0的周长,则mn的取值可能是( )
A. B.-
C. D.2
答案ABC
[可知直线mx+2ny-4=0过圆心(2,1),
有2m+2n-4=0,即n=2-m,则mn=m·(2-m)=-m2+2m=-(m-1)2+1≤1.]
12.设有一组圆Ck:(x-k+1)2+(y-3k)2=2k4(k∈N*).下列四个命题中是真命题的有( )
A.存在一条定直线与所有的圆均相切
B.存在一条定直线与所有的圆均相交
C.存在一条定直线与所有的圆均不相交
D.所有的圆均不经过原点
答案BD
根据题意得,圆心(k-1,3k),圆心在直线y=3(x+1)上,故存在直线y=3(x+1)与所有圆都相交,选项B正确;
考虑两圆的位置关系,
圆Ck:圆心(k-1,3k),半径为r=k2,
圆Ck+1:圆心(k-1+1,3(k+1)),
即(k,3k+3),半径为R=(k+1)2,
两圆的圆心距d=,两圆的半径之差R-r=(k+1)2-k2=2k+,任取k=1或2时,(R-r>d),Ck含于Ck+1之中,选项A错误;
若k取无穷大,则可以认为所有直线都与圆相交,选项C错误;
将(0,0)代入圆的方程,则有(-k+1)2+9k2=2k4,
即10k2-2k+1=2k4(k∈N*),
因为左边为奇数,右边为偶数,故不存在k使上式成立,即所有圆均不过原点,选项D正确.
13.若经过点(m,3)和(2,m)的直线l与斜率为-4的直线互相垂直,则m的值是 .
由题意可知kl=,又因为kl=,
所以,解得m=.
14.若点P(5a+1,12a)在圆(x-1)2+y2=1的外部,则a的取值范围为 .
答案a>或a<-
[∵P在圆外,∴(5a+1-1)2+(12a)2>1,169a2>1,a2>,∴|a|>,即a>或a<-.]
15.设PA⊥Rt△ABC所在的平面α,∠BAC=90°,PB,PC分别与α成45°和30°角,PA=2,则PA与BC的距离是 ;点P到BC的距离是 .
答案
作AD⊥BC于点D,
∵PA⊥面ABC,
∴PA⊥AD.∴AD是PA与BC的公垂线.
易得AB=2,AC=2,BC=4,AD=,连接PD,则PD⊥BC,P到BC的距离PD=.
16.已知向量m=(a,b,0),n=(c,d,1),其中a2+b2=c2+d2=1,现有以下命题:
①向量n与z轴正方向的夹角恒为定值(即与c,d无关);
②m·n的最大值为;
③
④若定义u×v=|u|·|v|sin
其中正确的命题有 .(写出所有正确命题的序号)
答案①③④
①取z轴的正方向单位向量a=(0,0,1),
则cos
②m·n=ac+bd≤=1,
当且仅当a=c,b=d时取等号,因此m·n的最大值为1,命题错误;
③由②可得|m·n|≤1,∴-1≤m·n≤1,
∴cos
=≥-=-,
∴
④由③可知:-≤cos
∴≤
综上可知,正确的命题序号是①③④.
17.已知空间中三点A(2,0,-2),B(1,-1,-2),C(3,0,-4),设a=,b=.
(1)若|c|=3,且c∥,求向量c;
(2)已知向量ka+b与b互相垂直,求k的值;
(3)求△ABC的面积.
(1)∵空间中三点A(2,0,-2),B(1,-1,-2),C(3,0,-4),设a=,b=,
∴=(3,0,-4)-(1,-1,-2)=(2,1,-2),
∵|c|=3,且c∥,
∴c=m=m(2,1,-2)=(2m,m,-2m),
∴|c|==3|m|=3,
∴m=±1,∴c=(2,1,-2)或c=(-2,-1,2).
(2)由题得a=(-1,-1,0),b=(1,0,-2),
∴ka+b=k(-1,-1,0)+(1,0,-2)=(1-k,-k,-2),
∵向量ka+b与b互相垂直,∴(ka+b)·b=1-k+4=0,解得k=5.∴k的值是5.
(3)=(-1,-1,0),=(1,0,-2),=(2,1,-2),
cos<>==-,sin<>=,
∴S△ABC=×||×||×sin<>=.
18.如图,在等腰梯形ABCD中,AB∥CD,边AB所在直线方程为2x-y-2=0,点C(2,0),|BC|=1,B为第一象限上的点.
(1)求点B坐标;
(2)求AB边上的高CE所在直线的方程;
(3)求直线AB与直线CD之间的距离.
(1)设B(a,2a-2),∵C(2,0),|BC|=1,
∴=1,解得a=1或a=.
∵B为第一象限上的点,∴2a-2>0,即a>1.
∴a=,则B.
(2)∵边AB所在直线方程为2x-y-2=0,
∴kCE=-=-.
又∵CE经过点C(2,0),∴AB边上的高CE所在直线的方程为y=-x+1,即x+2y-2=0.
(3)∵AB∥CD,∴kCD=kAB=2.
∵点C(2,0),
∴直线CD的方程为y=2(x-2),
即2x-y-4=0.
又AB所在直线方程为2x-y-2=0,
则直线AB与直线CD之间的距离d=.
19.已知圆C的方程可以表示为x2+y2-2x-4y+m=0,其中m∈R.
(1)若m=1,求圆C被直线x+y-1=0截得的弦长;
(2)若圆C与直线l:x+2y-4=0相交于M,N两点,且OM⊥ON(O为坐标原点),求m的值.
(1)m=1,配方得(x-1)2+(y-2)2=4,圆心到直线的距离为,
所以圆C被直线x+y-1=0截得的弦长为2=2.
(2)设M(x1,y1),N(x2,y2),
直线代入圆的方程得5x2-8x+4(m-4)=0,
所以x1+x2=,x1x2=.
因为OM⊥ON,所以x1x2+y1y2=0,
所以+4=0,
所以m=,此时Δ>0.
20.已知直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)和圆C:x2+y2-8x-6y+5=0.
(1)求证:直线l恒过一定点M;
(2)试求当m为何值时,直线l被圆C所截得的弦长最短;
(3)在(2)的前提下,直线l'是过点N(-1,-2)且与直线l平行的直线,求圆心在直线l'上,且与圆C相外切的动圆中半径最小的圆的标准方程.
(1)由直线l:(2m+1)x+(m+1)y-7m-4=0,得m(2x+y-7)+x+y-4=0,
联立解得
∴直线l恒过一定点M(3,1).
(2)要使直线l被圆C所截得的弦长最短,则l⊥CM,
化圆C:x2+y2-8x-6y+5=0为(x-4)2+(y-3)2=20,可得C(4,3),则kCM==2,
∴-=-,解得m=-.
(3)由(2)得,直线l':y+2=-(x+1),即x+2y+5=0.
如图,过C与直线x+2y+5=0垂直的直线方程为y-3=2(x-4),即2x-y-5=0.
联立
解得
而C到直线x+2y+5=0的距离d==3,
∴所求圆的半径为3-2.
故圆心在直线l'上,且与圆C相外切的动圆中半径最小的圆的标准方程为(x-1)2+(y+3)2=5.
21.如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
(1)求证:AB∥GH;
(2)求平面DGH与平面GHE的夹角的余弦值.
(1)因为D,C,E,F分别是AQ,BQ,AP,BP的中点,所以EF∥AB,DC∥AB.所以EF∥DC.
又EF 平面PCD,DC 平面PCD,
所以EF∥平面PCD.
又EF 平面EFQ,平面EFQ∩平面PCD=GH,
所以EF∥GH.又EF∥AB,所以AB∥GH.
(2)在△ABQ中,AQ=2BD,AD=DQ,
所以∠ABQ=90°.
又PB⊥平面ABQ,所以BA,BQ,BP两两垂直.
以B为坐标原点,分别以BA,BQ,BP所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
设BA=BQ=BP=2,
则E(1,0,1),F(0,0,1),Q(0,2,0),D(1,1,0),C(0,1,0),P(0,0,2).
所以=(-1,2,-1),=(0,2,-1),
=(-1,-1,2),=(0,-1,2).
设平面EFQ的一个法向量为m=(x1,y1,z1),
由m·=0,m·=0,
得取y1=1,得m=(0,1,2).
设平面PDC的一个法向量为n=(x2,y2,z2),
由n·=0,n·=0,
得取z2=1,得n=(0,2,1).
设平面DGH与平面GHE的夹角为θ,
则cosθ=|cos
22.(12分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=AD=1,CD=.
(1)求证:平面PBC⊥平面PQB;
(2)当PM的长为何值时,平面QMB与平面PDC所成的角的大小为60°
(1)∵AD∥BC,Q为AD的中点,BC=AD,
∴BC∥QD,BC=QD,
∴四边形BCDQ为平行四边形,∴BQ∥CD.
∵∠ADC=90°,∴BC⊥BQ.
∵PA=PD,AQ=QD,∴PQ⊥AD.
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PQ⊥平面ABCD,∴PQ⊥BC.
又∵PQ∩BQ=Q,∴BC⊥平面PQB.
∵BC 平面PBC,∴平面PBC⊥平面PQB.
(2)由(1)可知PQ⊥平面ABCD.如图,以Q为原点,分别以QA,QB,QP所在直线为x轴,y轴,z轴,建立空间直角坐标系,则Q(0,0,0),D(-1,0,0),P(0,0,),B(0,,0),C(-1,,0),
∴=(0,,0),=(0,,0),=(1,0,),=(-1,,-),
PC=.
设=λ,则=(-λ,λ,-λ),且0≤λ≤1,得M(-λ,λ,λ),
∴=(-λ,λ,(1-λ)).
设平面MBQ的法向量为m=(x,y,z),则
令x=,则y=0,z=,∴平面MBQ的一个法向量为m=,0,.
设平面PDC的法向量为n=(x',y',z'),则
令x'=3,则y'=0,z'=-,∴平面PDC的一个法向量为n=(3,0,-).
∴平面QMB与平面PDC所成的锐二面角的大小为60°,
∴cos60°=,
∴λ=.∴PM=PC=.即当PM=时,平面QMB与平面PDC所成的角大小为60°.
同课章节目录
