相似多边形

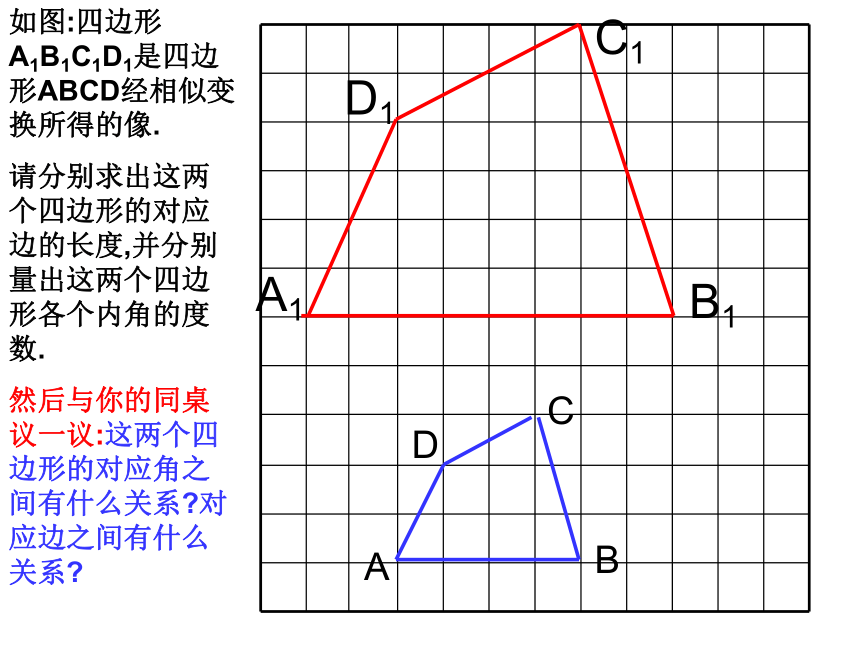
课件11张PPT。相似多边形ABCDA1B1C1D1如图:四边形A1B1C1D1是四边形ABCD经相似变换所得的像.
请分别求出这两个四边形的对应边的长度,并分别量出这两个四边形各个内角的度数.
然后与你的同桌议一议:这两个四边形的对应角之间有什么关系?对应边之间有什么关系? 对应角相等、对应边成比例的两个多边形叫做相似多边形.相似多边形对应顶点的字母应写在对应的位置上正方形1010菱形1212它们相似吗？正方形1010矩形128正方形正方形(1)(2)(3)练习;
书本P120 课内练习1 如果两个多边形相似，那么它们的对应角有什么关系？对应边呢？ 相似多边形的对应角相等，对应边成比例.相似多边形的性质1:练习:书本P120课内练习 2 ,3 相似多边形对应边的比叫做相似比.(1)四边形A1B1C1D1∽四边形ABCD,相似比为k.求四边形 A1B1C1D1与四边形ABCD的周长比.(2)连结A1C1,AC,所得的⊿A1B1C1与⊿ABC相似吗? ⊿A1D1C1与⊿ADC呢?如果相似,它们的相似比相等吗?为什么?(3)四边形A1B1C1D1与四边形ABCD的面积比与相似比有什么关系?性质2: 相似多边形的周长之比等于相似比;面积之比等于相似比的平方.练一练:
在比例尺为1:100000的地图上,某开发区的图上周长为25cm,图上面积为25cm2,那么该开发区的实际周长和实际面积分别是多少? 例：矩形纸张的长与宽的比为 ,对开后所得的矩形纸张是否与原来的矩形纸张相似?请说明理由.解：对开后所得的矩形纸张和原来的矩形纸张相似，理由如下：设原来的纸张为矩形ＡＢＣＤ，如图：连结ＢＣ与ＡＤ的中点Ｆ，Ｅ，则ＥＦ就把矩形ＡＢＣＤ分为全等的两个矩形．在矩形ＡＢＣＤ中，∴ 矩形ＡＢＦＥ与矩形ＢＣＤＡ的对应角相等，对应边成比例∴ 矩形ＡＢＦＥ与矩形ＢＣＤＡ相似可以发现，这些叠放起来的矩形的右上顶点同在一直线上，这是因为这些小矩形都是相似的，所以它们的长与宽对应成比例，（１）（２）如果以图（１）最大矩形的左下顶点为原点，宽和长所在直线分别为x轴、y轴，那么这组矩形右上顶点的坐标都满足把标准纸（长与宽之比为　）一次又一次对开如右图叠起来，你发现了什么有趣的现象？你能给出数学解释吗？　　　　探究活动谈谈收获1.相似多边形的定义2.相似多边形的性质性质1:相似多边形的对应角相等，对应边成比例. 对应角相等、对应边成比例的两个多边形 叫做相似多边形.性质2: 相似多边形的周长之比等于相似比;面积之比等于相似比的平方.1、右边两个矩形相似，求它们的相似比.2、如图，两个正六边形的边长分别为a和b，它们相似吗？为什么？相似比为多少?３、如图，矩形的草坪长20m，宽10m，沿草坪四周外围有1m的环行小路，小路的内外边缘所成的矩形相似吗？2∶3相似.理由是：各对应角相等，各对应边成比例. 不相似.因为对应边不成比例.练一练：