24.2.2直线与圆的位置关系(第三课时)
文档属性
| 名称 | 24.2.2直线与圆的位置关系(第三课时) |

|
|
| 格式 | rar | ||
| 文件大小 | 121.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-27 00:00:00 | ||
图片预览




文档简介
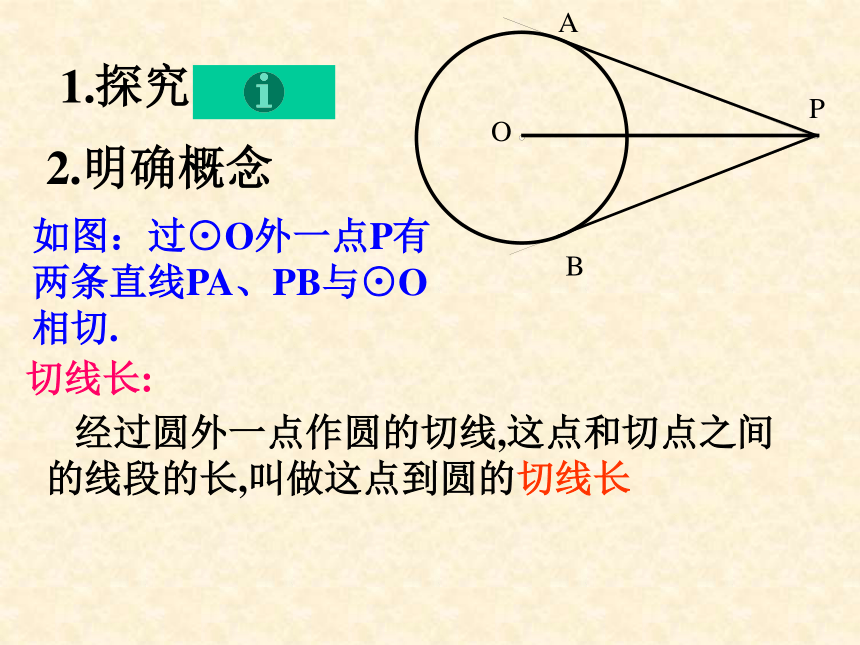
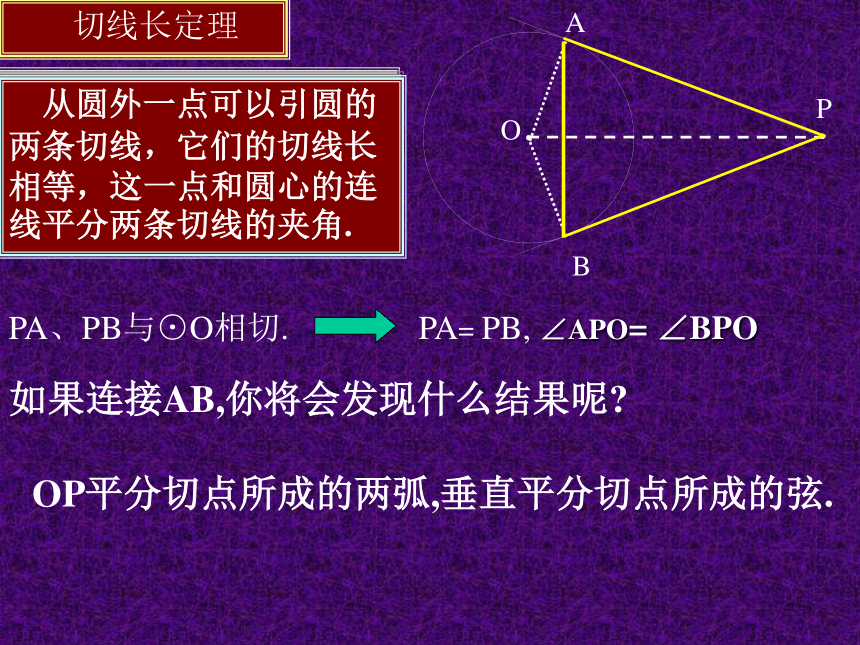
课件14张PPT。直线与圆的位置关系第三课时(圆的切线长定理)2.切线有那些性质1.过圆心2.过切点3.垂直于切线任意两个作为条件就能推第三个结论证明直线是圆的切线的方法有:1.利用定义(当直线和圆有唯一公共点时)2.用圆心到直线的距离等于圆的半径3.切线的判定:过半径的外端垂直于半径的直线是圆的切线温故知新1.探究2.明确概念 经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长切线长:如图:过⊙O外一点P有两条直线PA、PB与⊙O相切. 切线长定理 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.OP平分切点所成的两弧,垂直平分切点所成的弦.ABPO如果连接AB,你将会发现什么结果呢?例1已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O 于点 D、E,交 AB 于 C.
(1)写出图中所有的垂直关系;
(2)写出图中所有的全等三角形.
(3)如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.AOCDPBE解:(1) OA⊥PA , OB⊥PB , OP⊥AB(2) △OAP ≌△ OBP , △OCA≌△OCB , △ACP≌△BCP.(3) 设 OA = x cm , 则 PO = PD + x = 2 + x (cm) 在 Rt△OAP 中,由勾股定理,得 PA 2 + OA 2 = OP 2 即 4 2 + x 2 = (x + 2 ) 2 解得 x = 3 cm 所以,半径 OA 的长为 3 cm. 变式题已知,如图,PA、PB是⊙O的两条切线,A、B为切点.若∠APB=60o,PO=2.
(1)求∠APO, ∠AOB的度数.
(2)求切线PA的长.
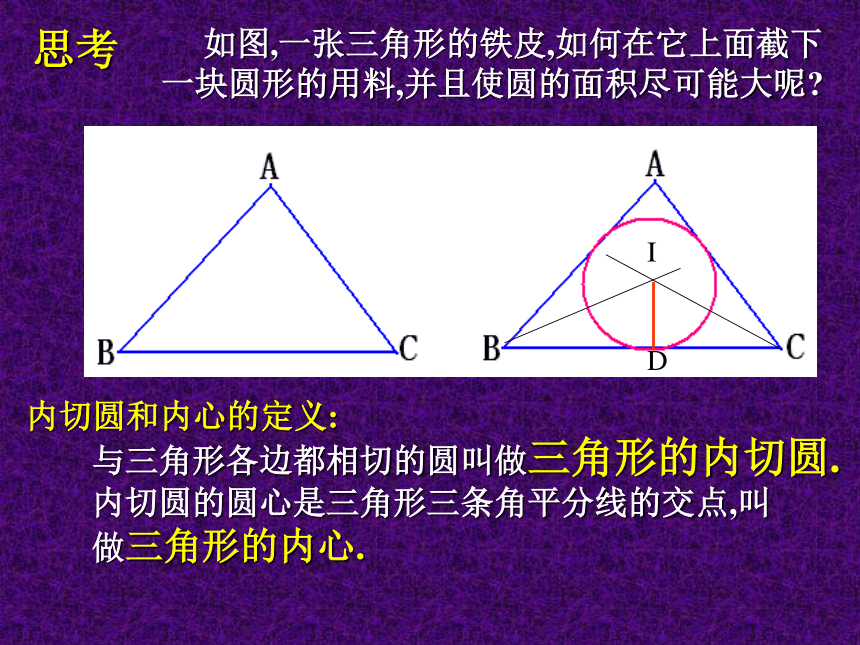
(3)连接AB,试问PO与AB有什么关系.OBAP思考 如图,一张三角形的铁皮,如何在它上面截下
一块圆形的用料,并且使圆的面积尽可能大呢?ID内切圆和内心的定义:与三角形各边都相切的圆叫做三角形的内切圆.
内切圆的圆心是三角形三条角平分线的交点,叫
做三角形的内心.例2 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
求AF、BD、CE的长.解法一:设AF=x(cm),则AE=x(cm)∴CD=CE=AC-AE=13-x
BD=BF=AB-AF=9-x由 BD+CD=BC可得
(13-x)+(9-x)=14解得 x=4∴ AF=4(cm), BD=5(cm), CE=9(cm).例2 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
求AF、BD、CE的长.练习 P106. 1. 2解法二:解得 x=4 y=5 z=9∴ AF=4(cm), BD=5(cm), CE=9(cm).记一记:2.既有外接圆,又内切圆的平行四边形是______.
3.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
4.⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.EFHG正方形22cm2cm练一练1. Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半径是_______.15.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢?小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出墙的直径,请你利用图乙,说
明她这样做的道理.O想一想:圆的外切四边形的两组对边有什么关系?说明你的结论的正确性.ABCDOLMNP答:利用切线长定理就可出:AB+CD=AD+CB本节课我有什么收获?小 结请 与 同 学 们 分 享 !
(1)写出图中所有的垂直关系;
(2)写出图中所有的全等三角形.
(3)如果 PA = 4 cm , PD = 2 cm , 求半径 OA 的长.AOCDPBE解:(1) OA⊥PA , OB⊥PB , OP⊥AB(2) △OAP ≌△ OBP , △OCA≌△OCB , △ACP≌△BCP.(3) 设 OA = x cm , 则 PO = PD + x = 2 + x (cm) 在 Rt△OAP 中,由勾股定理,得 PA 2 + OA 2 = OP 2 即 4 2 + x 2 = (x + 2 ) 2 解得 x = 3 cm 所以,半径 OA 的长为 3 cm. 变式题已知,如图,PA、PB是⊙O的两条切线,A、B为切点.若∠APB=60o,PO=2.
(1)求∠APO, ∠AOB的度数.
(2)求切线PA的长.
(3)连接AB,试问PO与AB有什么关系.OBAP思考 如图,一张三角形的铁皮,如何在它上面截下
一块圆形的用料,并且使圆的面积尽可能大呢?ID内切圆和内心的定义:与三角形各边都相切的圆叫做三角形的内切圆.
内切圆的圆心是三角形三条角平分线的交点,叫
做三角形的内心.例2 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
求AF、BD、CE的长.解法一:设AF=x(cm),则AE=x(cm)∴CD=CE=AC-AE=13-x
BD=BF=AB-AF=9-x由 BD+CD=BC可得
(13-x)+(9-x)=14解得 x=4∴ AF=4(cm), BD=5(cm), CE=9(cm).例2 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
求AF、BD、CE的长.练习 P106. 1. 2解法二:解得 x=4 y=5 z=9∴ AF=4(cm), BD=5(cm), CE=9(cm).记一记:2.既有外接圆,又内切圆的平行四边形是______.
3.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
4.⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.EFHG正方形22cm2cm练一练1. Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半径是_______.15.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢?小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出墙的直径,请你利用图乙,说
明她这样做的道理.O想一想:圆的外切四边形的两组对边有什么关系?说明你的结论的正确性.ABCDOLMNP答:利用切线长定理就可出:AB+CD=AD+CB本节课我有什么收获?小 结请 与 同 学 们 分 享 !
同课章节目录
