人教版数学九年级上册24.1.2 垂直于弦的直径 课件(共19张ppt)
文档属性
| 名称 | 人教版数学九年级上册24.1.2 垂直于弦的直径 课件(共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 392.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 20:30:37 | ||
图片预览






文档简介
(共19张PPT)
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
学习目标
1.理解圆的对称性;掌握垂径定理.
2.利用垂直于弦的直径的性质解决相关实际问题.
证明:如图,设CD是⊙O的任意一条直径,A为⊙O上点C,D以外的任意一点.过点A作AB⊥CD,交⊙O于点B,垂足为M,连接OA,OB.
在△OAB中,∵OA=OB,∴△OAB是等腰三角形.
又AB⊥CD,∴AM=BM.
即CD是AB的垂直平分线.这就是说,对于圆上
任意一点A,在圆上都有关于直线CD的对称点B,因此,
⊙O关于直线CD对称.即圆是轴对称图形,任何一条直
径所在直线都是它的对称轴.
证明圆的对称性
合作探究,形成知识
按下面的步骤做一做:
第一步,在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合;
第二步,得到一条折痕CD;
第三步,在⊙O上任取一点A,过点A作折痕CD的垂线,垂足为点M;
第四步,将纸打开,设AM的延长线与圆交于另一点B.
在上述的操作过程中,你发现了哪些相等的线段和相等的弧 为什么?
合作探究,形成知识
即直径CD平分弦AB,并且平分弧AB及弧ACB
这个定理也叫垂径定理。
垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
平分弦(不是直径)的直径垂直于弦,
并且平分弦所对的两条弧.
合作探究,形成知识
AE=BE, = , =
AD
(
BD
(
AC
(
BC
(
垂径定理的证明:
合作探究,形成知识
证明:如图所示,连接OA,OB,得到等腰△OAB,即OA=OB.
因为CD⊥AB,
所以△OAM与△OBM都是直角三角形.
又因为OM为公共边,
所以这两个直角三角形全等.所以AM=BM.
又因为⊙O关于直径CD所在的直线对称,
所以A点和B点关于直线CD对称.
所以当圆沿着直径CD对折时,
点A与点B重合,弧AC与弧BC重合.因此AM=BM,弧AC与弧BC,同理可得到弧AD与弧BD.
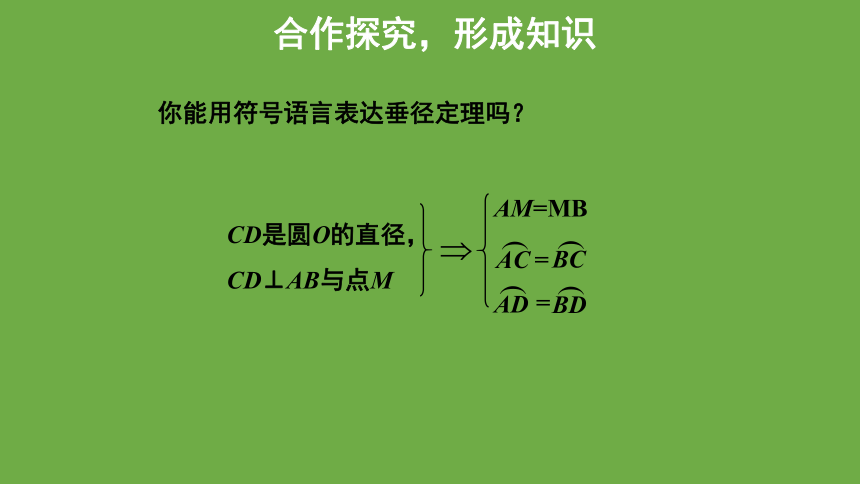
你能用符号语言表达垂径定理吗?
合作探究,形成知识
CD是圆O的直径,
CD⊥AB与点M
AM=MB
AC
(
BC
(
AD
(
BD
(
=
=
例1 如图, 所在圆的圆心是点O,过O作OC⊥AB于点D.若CD=4 m,弦AB=16 m,求此圆的半径.
解:设圆的半径为R,
由题意可得OD=R-4,AD=8 m.
在Rt△ADO中,AO2=OD2+AD2,
即R2=(R-4)2+82.
解得R=10(m).
答:此圆的半径是10 m.
例题应用,深化提高
AB
(
例2 如图,赵州桥是我国隋代建造的石拱桥,距今约有1 400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37 m,拱高(弧的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
例题应用,深化提高
【教学图片】《二次函数》图片6赵州桥的图片,用于教学过程。
解得R≈27.3(m).
O
D
A
B
C
R
在Rt△OAD中,由勾股定理,得
即R2=18.52+(R-7.23)2.
因此,赵州桥的主桥拱半径约为27.3 m.
OA2=AD2+OD2,
由题设可知,AB=37 m,CD=7.23 m,所以
OD=OC-CD=R-7.23.
解:如图,用弧AB表示主桥拱,设弧AB所在圆的圆心为O,半径为R.经过圆心O作弦AB的垂线OC,D为垂足,OC与弧AB相交于点C,连接OA.根据垂径定理,D是AB的中点,C是弧AB的中点,CD就是拱高.
例题应用,深化提高
练习巩固,综合应用
1.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP︰AP=1︰5,则CD的长为( ).
D
练习巩固,综合应用
2.如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为______cm.
3.⊙O的直径为10,弦AB的长为8,P是弦AB上的一个动点,则OP长的取值范围为 .
3≤OP≤5
.
4.已知⊙O中,若弦AB的长为8 cm,圆心O到AB的距离为3 cm,求⊙O的半径.
解:连结OA,过O作OE⊥AB,
垂足为E,则OE=3 cm,AE=BE.
∵AB=8 cm,∴AE=4 cm.
在Rt△AOE中,根据勾股定理可得OA=5 cm.
∴⊙O的半径为5 cm.
A
E
B
O
练习巩固,综合应用
练习巩固,综合应用
5.如图,AB是⊙O的直径,作半径OA的垂直平分线,交⊙O于C,D两点,垂足为H,连接BC,BD.
(1)求证:BC=BD;
(2)若CD=6,求⊙O的半径长.
解:(1)连接OC.
∵AB是⊙O的直径,且AB⊥CD,
∴CH=DH,BC=BD.
练习巩固,综合应用
(2)连接OC.
∵CD平分OA,设⊙O的半径为r,
则OH= r.
∵CD=6,
∴CH= CD=3.
∵∠CHO=90°,
∴OH2+CH2=CO2,即( r)2+32=r2.
∴r=2 .
故⊙O的半径长是2 .
6.银川市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如下图所示,污水水面宽度为60 cm,水面至管道顶部距离为10 cm,问修理人员应准备内径多大的管道
练习巩固,综合应用
练习巩固,综合应用
解:如图所示,连接OA,过点O作OE⊥AB,垂足为E,交圆于点F,则AE= AB=30 cm.
令⊙O的半径为R cm,则OA=R cm ,OE=OF-EF=(R-10)cm.
在Rt△AEO中,OA2=AE2+OE2,即R2=302+(R-10)2.
解得R =50.
所以修理人员应准备内径为100 cm的管道.
圆的轴对称性;垂径定理及其推论.
(1)垂径定理和勾股定理的结合;
(2)在圆中解决与弦有关的问题时常作的辅助线:
——过圆心作垂直于弦的线段;
——连接半径.
课堂小结
再见
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
学习目标
1.理解圆的对称性;掌握垂径定理.
2.利用垂直于弦的直径的性质解决相关实际问题.
证明:如图,设CD是⊙O的任意一条直径,A为⊙O上点C,D以外的任意一点.过点A作AB⊥CD,交⊙O于点B,垂足为M,连接OA,OB.
在△OAB中,∵OA=OB,∴△OAB是等腰三角形.
又AB⊥CD,∴AM=BM.
即CD是AB的垂直平分线.这就是说,对于圆上
任意一点A,在圆上都有关于直线CD的对称点B,因此,
⊙O关于直线CD对称.即圆是轴对称图形,任何一条直
径所在直线都是它的对称轴.
证明圆的对称性
合作探究,形成知识
按下面的步骤做一做:
第一步,在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合;
第二步,得到一条折痕CD;
第三步,在⊙O上任取一点A,过点A作折痕CD的垂线,垂足为点M;
第四步,将纸打开,设AM的延长线与圆交于另一点B.
在上述的操作过程中,你发现了哪些相等的线段和相等的弧 为什么?
合作探究,形成知识
即直径CD平分弦AB,并且平分弧AB及弧ACB
这个定理也叫垂径定理。
垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
平分弦(不是直径)的直径垂直于弦,
并且平分弦所对的两条弧.
合作探究,形成知识
AE=BE, = , =
AD
(
BD
(
AC
(
BC
(
垂径定理的证明:
合作探究,形成知识
证明:如图所示,连接OA,OB,得到等腰△OAB,即OA=OB.
因为CD⊥AB,
所以△OAM与△OBM都是直角三角形.
又因为OM为公共边,
所以这两个直角三角形全等.所以AM=BM.
又因为⊙O关于直径CD所在的直线对称,
所以A点和B点关于直线CD对称.
所以当圆沿着直径CD对折时,
点A与点B重合,弧AC与弧BC重合.因此AM=BM,弧AC与弧BC,同理可得到弧AD与弧BD.
你能用符号语言表达垂径定理吗?
合作探究,形成知识
CD是圆O的直径,
CD⊥AB与点M
AM=MB
AC
(
BC
(
AD
(
BD
(
=
=
例1 如图, 所在圆的圆心是点O,过O作OC⊥AB于点D.若CD=4 m,弦AB=16 m,求此圆的半径.
解:设圆的半径为R,
由题意可得OD=R-4,AD=8 m.
在Rt△ADO中,AO2=OD2+AD2,
即R2=(R-4)2+82.
解得R=10(m).
答:此圆的半径是10 m.
例题应用,深化提高
AB
(
例2 如图,赵州桥是我国隋代建造的石拱桥,距今约有1 400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37 m,拱高(弧的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
例题应用,深化提高
【教学图片】《二次函数》图片6赵州桥的图片,用于教学过程。
解得R≈27.3(m).
O
D
A
B
C
R
在Rt△OAD中,由勾股定理,得
即R2=18.52+(R-7.23)2.
因此,赵州桥的主桥拱半径约为27.3 m.
OA2=AD2+OD2,
由题设可知,AB=37 m,CD=7.23 m,所以
OD=OC-CD=R-7.23.
解:如图,用弧AB表示主桥拱,设弧AB所在圆的圆心为O,半径为R.经过圆心O作弦AB的垂线OC,D为垂足,OC与弧AB相交于点C,连接OA.根据垂径定理,D是AB的中点,C是弧AB的中点,CD就是拱高.
例题应用,深化提高
练习巩固,综合应用
1.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP︰AP=1︰5,则CD的长为( ).
D
练习巩固,综合应用
2.如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为______cm.
3.⊙O的直径为10,弦AB的长为8,P是弦AB上的一个动点,则OP长的取值范围为 .
3≤OP≤5
.
4.已知⊙O中,若弦AB的长为8 cm,圆心O到AB的距离为3 cm,求⊙O的半径.
解:连结OA,过O作OE⊥AB,
垂足为E,则OE=3 cm,AE=BE.
∵AB=8 cm,∴AE=4 cm.
在Rt△AOE中,根据勾股定理可得OA=5 cm.
∴⊙O的半径为5 cm.
A
E
B
O
练习巩固,综合应用
练习巩固,综合应用
5.如图,AB是⊙O的直径,作半径OA的垂直平分线,交⊙O于C,D两点,垂足为H,连接BC,BD.
(1)求证:BC=BD;
(2)若CD=6,求⊙O的半径长.
解:(1)连接OC.
∵AB是⊙O的直径,且AB⊥CD,
∴CH=DH,BC=BD.
练习巩固,综合应用
(2)连接OC.
∵CD平分OA,设⊙O的半径为r,
则OH= r.
∵CD=6,
∴CH= CD=3.
∵∠CHO=90°,
∴OH2+CH2=CO2,即( r)2+32=r2.
∴r=2 .
故⊙O的半径长是2 .
6.银川市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如下图所示,污水水面宽度为60 cm,水面至管道顶部距离为10 cm,问修理人员应准备内径多大的管道
练习巩固,综合应用
练习巩固,综合应用
解:如图所示,连接OA,过点O作OE⊥AB,垂足为E,交圆于点F,则AE= AB=30 cm.
令⊙O的半径为R cm,则OA=R cm ,OE=OF-EF=(R-10)cm.
在Rt△AEO中,OA2=AE2+OE2,即R2=302+(R-10)2.
解得R =50.
所以修理人员应准备内径为100 cm的管道.
圆的轴对称性;垂径定理及其推论.
(1)垂径定理和勾股定理的结合;
(2)在圆中解决与弦有关的问题时常作的辅助线:
——过圆心作垂直于弦的线段;
——连接半径.
课堂小结
再见
同课章节目录
