人教版九年级上册24.2.2 直线和圆的位置关系教学课件(第3课时) 22张PPT
文档属性
| 名称 | 人教版九年级上册24.2.2 直线和圆的位置关系教学课件(第3课时) 22张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 712.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 20:38:47 | ||
图片预览






文档简介
(共22张PPT)
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第3课时)
学习目标
1.理解切线长的概念和三角形内切圆、内心的概念.
2.掌握切线长定理及其应用.
知识回顾,引入新课
切线的判定定理和性质定理是什么?
(透明纸上画出⊙O,并画出过⊙O上A点的
切线PA,连接PO)沿着直线PO将纸对折,设
与点A重合的点为B.观察并思考:
①PB是⊙O的切线吗?
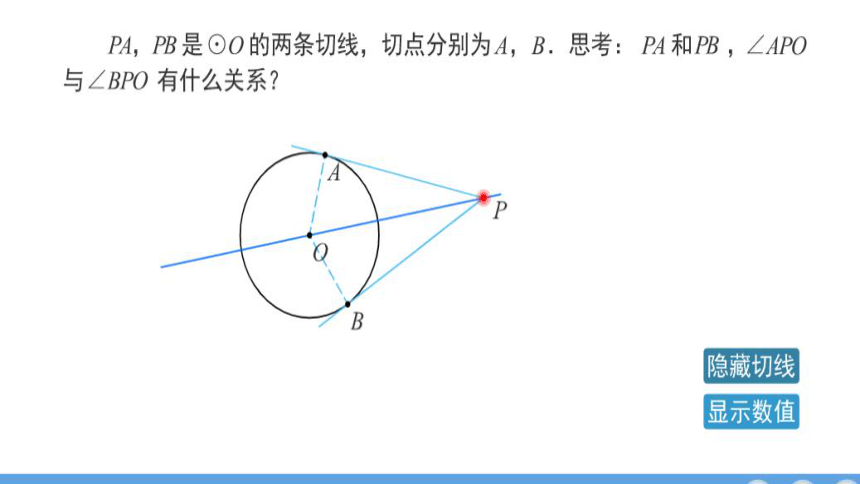
②判断图中的PA与PB,∠APO与∠BPO有什么
关系?
PA=PB,
∠APO=∠ BPO.
PB是⊙O的切线
合作探究,形成新知
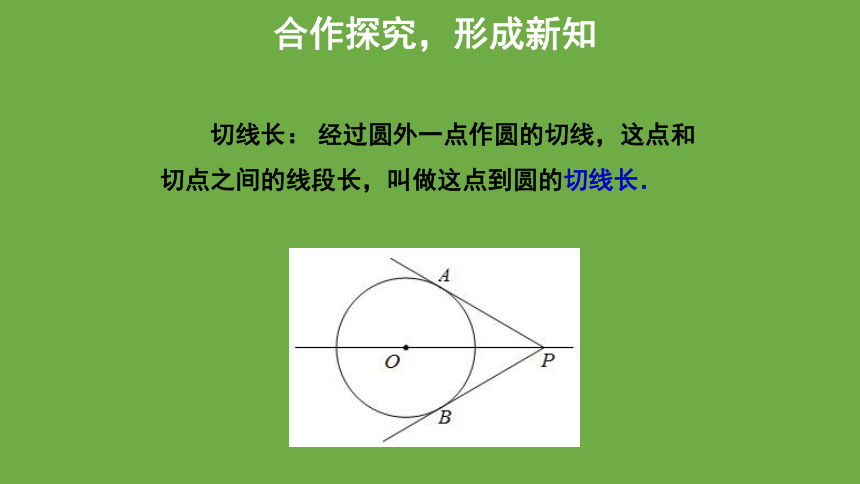
切线长: 经过圆外一点作圆的切线,这点和切点之间的线段长,叫做这点到圆的切线长.
合作探究,形成新知
求证: PA=PB,∠APO=∠ BPO.
证明:
∵PA、PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP.
又OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL),
∴PA=PB,∠1=∠2 .
合作探究,形成新知
切线
切线长
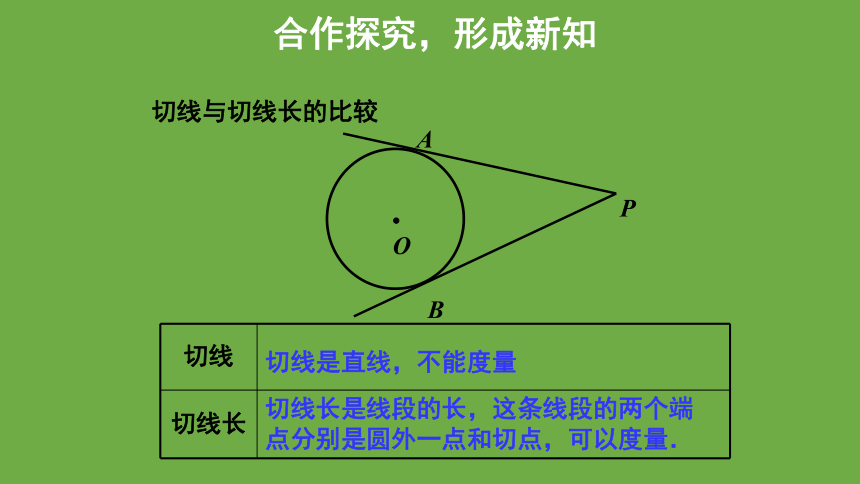
切线是直线,不能度量
切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
O
P
A
B
切线与切线长的比较
合作探究,形成新知
过圆外一点能做几条圆的切线?两条切线长怎样?相邻两个角相等可以视为∠APB被平分,怎样叙述?
从圆外一点可以引圆的两条切线,它们的切线
长相等,这一点和圆心的连线平分两条切线的夹角.
切线长定理:
合作探究,形成新知
用符号语言表示定理:
∵PA、PB分别是⊙O的切线,点A、B分别为切点,
∴PA=PB,∠APO=∠BPO.
合作探究,形成新知
问题1 作圆的关键是什么?
确定圆心和半径.
问题2 怎样确定圆心的位置?
作两条角平分线,其交点就是圆心的位置.
问题3 圆心的位置确定后,怎样确定圆的半径?
过圆心作三角形一边的垂线,垂线段的长就是圆的半径.
下面是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三边都相切?请动手画一画.
合作探究,形成新知
已知△ABC,求作一个圆,使它与△ABC的三边都
相切.
作法:
1.作∠ABC、∠ACB的平分线BM和CN,交点为I;
2.过点I作ID⊥BC,垂足为D;
3.以I为圆心,ID为半径作⊙I,⊙I就是所求.
合作探究,形成新知
三角形的内切圆:
与三角形各边都相切的圆叫做三角形的内切圆.
三角形的内心:
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
合作探究,形成新知
例 △ABC 的内切圆 与 BC、CA、AB 分别相切于点 D、E、F,且 AB=9,BC=14,CA=13.求 AF,BD,CE 的长.
解: 设AF=x ,则AE=x,
CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x,
由BD+CD=BC可得
(9-x)+(13-x)=14.
解得x=4.
因此AF=4,BD=5,CE=9.
例题分析,深化提高
练习巩固,综合应用
1.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( ).
B
练习巩固,综合应用
2.如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,则∠P的度数是( ).
A.60° B.120° C.50° D.30°
3.如图,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是AB上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( ).
A.12 B.6 C.8 D.4
A
B
练习巩固,综合应用
4.如图,边长为a的正三角形的内切圆半径是( ).
A
5.如图, △ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠BOC的度数.
=117.5°
A
C
B
O
练习巩固,综合应用
解 :∠BOC=180°- (∠ABC +∠ACB)
=180°- (50°+75°)
6.△ABC的内切圆半径为r, △ABC的周长为l,求△ABC的面积.(提示:设内心为O,连接OA、OB、OC.)
解:设AB = c,BC = a,AC = b.
C
A
B
·
O
D
M
N
r
r
r
练习巩固,综合应用
则
切线长的定义:
经过圆外一点作圆的切线,这点和切点之间线段的长,叫做这点到圆的切线长.
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
用符号语言表示定理:
∵PA、PB分别是⊙O的切线,点A、B分别为切点,
∴PA=PB,∠APO=∠BPO.
课堂小结
三角形的内切圆:
与三角形各边都相切的圆叫做三角形的内切圆.
三角形的内心:
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
课堂小结
再见
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第3课时)
学习目标
1.理解切线长的概念和三角形内切圆、内心的概念.
2.掌握切线长定理及其应用.
知识回顾,引入新课
切线的判定定理和性质定理是什么?
(透明纸上画出⊙O,并画出过⊙O上A点的
切线PA,连接PO)沿着直线PO将纸对折,设
与点A重合的点为B.观察并思考:
①PB是⊙O的切线吗?
②判断图中的PA与PB,∠APO与∠BPO有什么
关系?
PA=PB,
∠APO=∠ BPO.
PB是⊙O的切线
合作探究,形成新知
切线长: 经过圆外一点作圆的切线,这点和切点之间的线段长,叫做这点到圆的切线长.
合作探究,形成新知
求证: PA=PB,∠APO=∠ BPO.
证明:
∵PA、PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP.
又OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL),
∴PA=PB,∠1=∠2 .
合作探究,形成新知
切线
切线长
切线是直线,不能度量
切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
O
P
A
B
切线与切线长的比较
合作探究,形成新知
过圆外一点能做几条圆的切线?两条切线长怎样?相邻两个角相等可以视为∠APB被平分,怎样叙述?
从圆外一点可以引圆的两条切线,它们的切线
长相等,这一点和圆心的连线平分两条切线的夹角.
切线长定理:
合作探究,形成新知
用符号语言表示定理:
∵PA、PB分别是⊙O的切线,点A、B分别为切点,
∴PA=PB,∠APO=∠BPO.
合作探究,形成新知
问题1 作圆的关键是什么?
确定圆心和半径.
问题2 怎样确定圆心的位置?
作两条角平分线,其交点就是圆心的位置.
问题3 圆心的位置确定后,怎样确定圆的半径?
过圆心作三角形一边的垂线,垂线段的长就是圆的半径.
下面是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三边都相切?请动手画一画.
合作探究,形成新知
已知△ABC,求作一个圆,使它与△ABC的三边都
相切.
作法:
1.作∠ABC、∠ACB的平分线BM和CN,交点为I;
2.过点I作ID⊥BC,垂足为D;
3.以I为圆心,ID为半径作⊙I,⊙I就是所求.
合作探究,形成新知
三角形的内切圆:
与三角形各边都相切的圆叫做三角形的内切圆.
三角形的内心:
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
合作探究,形成新知
例 △ABC 的内切圆 与 BC、CA、AB 分别相切于点 D、E、F,且 AB=9,BC=14,CA=13.求 AF,BD,CE 的长.
解: 设AF=x ,则AE=x,
CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x,
由BD+CD=BC可得
(9-x)+(13-x)=14.
解得x=4.
因此AF=4,BD=5,CE=9.
例题分析,深化提高
练习巩固,综合应用
1.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( ).
B
练习巩固,综合应用
2.如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,则∠P的度数是( ).
A.60° B.120° C.50° D.30°
3.如图,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是AB上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( ).
A.12 B.6 C.8 D.4
A
B
练习巩固,综合应用
4.如图,边长为a的正三角形的内切圆半径是( ).
A
5.如图, △ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠BOC的度数.
=117.5°
A
C
B
O
练习巩固,综合应用
解 :∠BOC=180°- (∠ABC +∠ACB)
=180°- (50°+75°)
6.△ABC的内切圆半径为r, △ABC的周长为l,求△ABC的面积.(提示:设内心为O,连接OA、OB、OC.)
解:设AB = c,BC = a,AC = b.
C
A
B
·
O
D
M
N
r
r
r
练习巩固,综合应用
则
切线长的定义:
经过圆外一点作圆的切线,这点和切点之间线段的长,叫做这点到圆的切线长.
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
用符号语言表示定理:
∵PA、PB分别是⊙O的切线,点A、B分别为切点,
∴PA=PB,∠APO=∠BPO.
课堂小结
三角形的内切圆:
与三角形各边都相切的圆叫做三角形的内切圆.
三角形的内心:
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
课堂小结
再见
同课章节目录
