人教版九年级数学上册 24.2.1点和圆的位置关系 (第1课时) 课件(共26张PPT)
文档属性
| 名称 | 人教版九年级数学上册 24.2.1点和圆的位置关系 (第1课时) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 954.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
24.2.1 点和圆的位置关系
第1课时
学习目标
1. 探索并掌握点和圆的位置关系,及这三种位置关系对应的圆的半径与点到圆心的距离之间的关系;
2. 了解三角形的外接圆和三角形的外心等概念;
3. 经历“不在同一直线上的三个点确定一个圆”的探索过程,培养学生的探索能力,进一步体会解决数学问题的策略;
4. 形成解决问题的一些基本策略,体验解决问题策略的多样性,发展实践能力与创新精神.
点和圆的位置关系
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察与思考
我国射击运动员在奥运会上屡获金牌,为我国赢得荣誉,图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
观察与思考
下图是一位射击运动员,六发子弹在射击靶上留下的痕迹.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察与思考
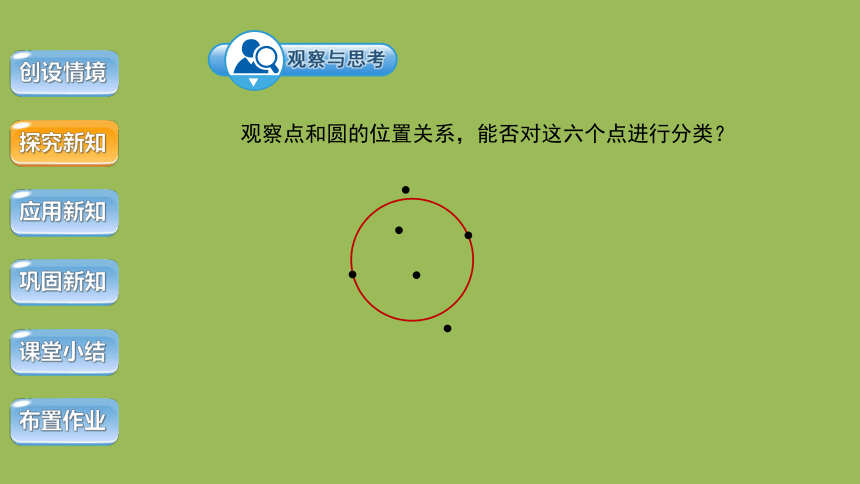
观察点和圆的位置关系,能否对这六个点进行分类?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
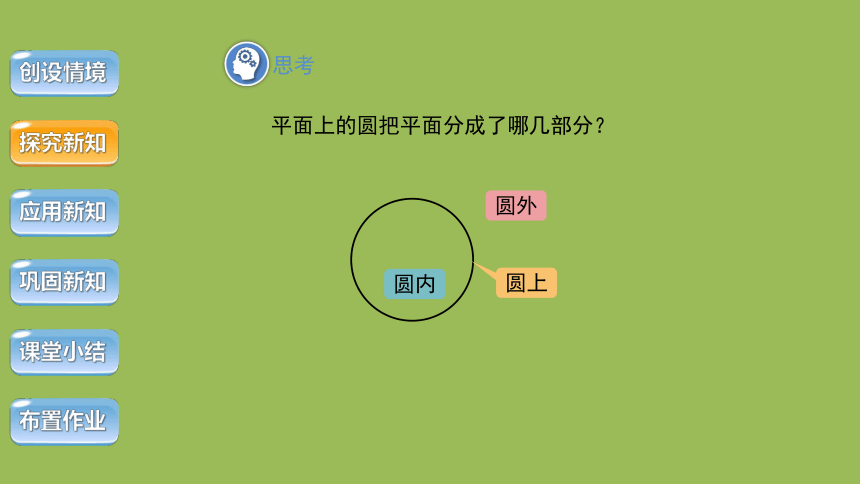
平面上的圆把平面分成了哪几部分?
圆内
圆外
圆上
思考
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
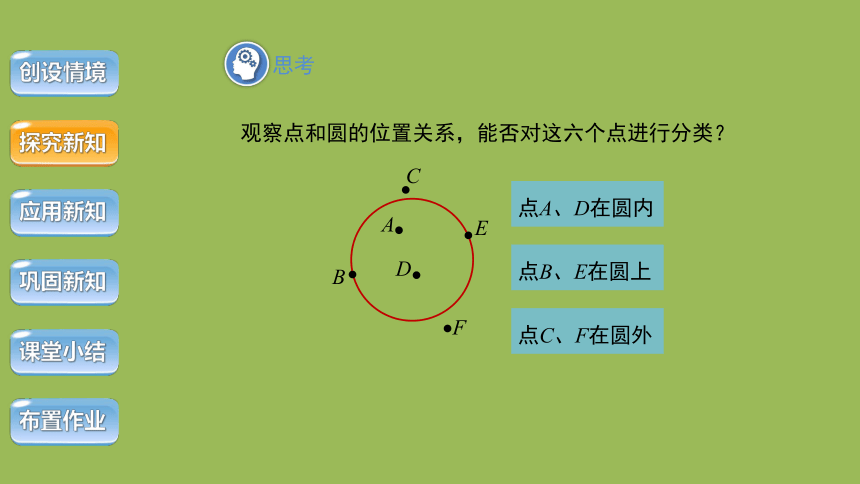
观察点和圆的位置关系,能否对这六个点进行分类?
B
C
A
D
E
F
点C、F在圆外
点A、D在圆内
点B、E在圆上
思考
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
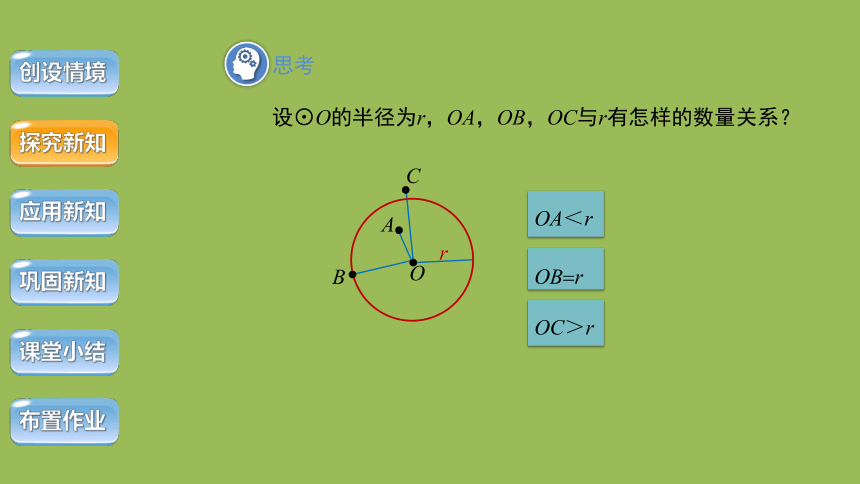
设⊙O的半径为r,OA,OB,OC与r有怎样的数量关系?
B
C
A
O
思考
OA<r
OB r
OC>r
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
r
点P在圆外
点P在圆内
点P在圆上
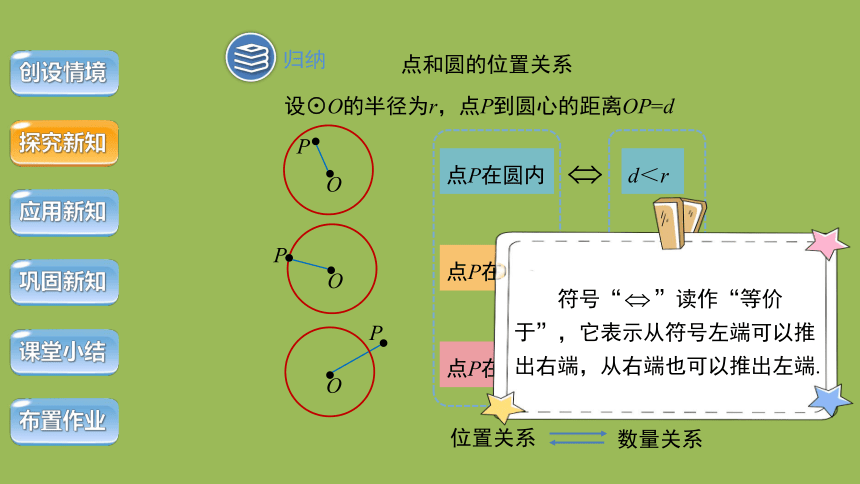
归纳
设⊙O的半径为r,点P到圆心的距离OP=d
P
O
P
O
P
O
d<r
d=r
d>r
位置关系
数量关系
点和圆的位置关系
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
符号“ ”读作“等价于”,它表示从符号左端可以推出右端,从右端也可以推出左端.
现在知道击中靶上不同位置的成绩是如何计算的吗?
射击成绩用弹着点位置对应的环数表示.弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击成绩越好.
想一想
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知⊙O的面积为25π:
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上;
(4)若点P不在圆外,则PO .
做一做
5
圆外
圆内
≤5
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
回忆一下作一个圆需要哪些条件?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
r
已知圆心和半径,可以作一个圆
确定一个圆需要几个点呢
两点确定一条直线.
已知圆心和半径,可以作一个圆,经过一个已知点A能不能作圆,这样的圆你能作出多少个?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
可作无数个圆
…
思考
经过两个已知点A,B能不能作圆?如果能,圆心分布有什么特点?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
可作无数个圆
∵所作圆的圆心到A,B的距离相等
∴圆心在线段AB的垂直平分线上
B
A
思考
经过不在同一条直线上的三个点A,B,C能否作圆?如果能,如何确定所作圆的圆心?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
A
B
C
分组讨论:
1.学生先分组进行讨论;
2.教师根据讨论情况作相应提示;
3.学生讲解思路,教师补充完善.
经过不在同一条直线上的三个点A,B,C能否作圆?如果能,如何确定所作圆的圆心?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
A
B
C
所作圆经过A,B,C三点
圆心O到A,B,C三点距离相等
圆心O在线段AB的垂直平分线上
圆心O也在线段BC的垂直平分线上
圆心O为两线段垂直平分线的交点
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
A
B
C
作法:
(1)分别作出线段AB,BC的垂直平分线l1,l2;
(2)l1与l2交于点O,
(3)圆O即为所作圆.
O
不在同一条直线上的三个点确定一个圆
l1
l2
经过不在同一条直线上的三个点A,B,C能否作圆?如果能,如何确定所作圆的圆心?
以点O为圆心,OA的长为
半径作圆;
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
A
B
C
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
O
l1
l2
拓展
外接圆圆心是三角形的三边的垂直平分线的交点,叫做这个三角形的外心.
△ABC的外接圆
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1.如图,在△ABC中,∠C=90°,AB=5 cm,BC=4 cm,以A为圆心,以3 cm为半径画圆,请判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
解:在△ABC中,由勾股定理得:
(1)∵AC=3 cm,∴点C在⊙A上.
(2)∵AB=5 cm>3 cm,∴点B在⊙A外.
(3)∵点D是AB的中点,∴AD=2.5 cm<3 cm,∴点D在⊙A内.
创设情境
3 cm
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2.某地出土一明代残破圆形瓷盘,如图所示.为复制该瓷盘确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心.
(不要求写作法、证明和讨论,但要保留作图痕迹)
A
B
C
O
创设情境
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.两个圆心为O的甲、乙两圆,半径分别为r1和r2,且r1<OA<r2,那么点A在( )
A.甲圆内 B.乙圆外
C.甲圆外,乙圆内 D.甲圆内,乙圆外
2.如果⊙O的半径为r,点P到圆心O的距离为6,那么
①点P在⊙O外,则r ;
②点P在 ,则r=6;
③点P在 ,则r>6.
C
<6
⊙O上
⊙O内
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
(2)若在△ABC中,AB=8 m,AC=6 m,∠BAC=90°,试求小明家圆形花坛的面积.
解:(1)如图所示,⊙O即为所求作的花坛的位置.
O
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
(2)若在△ABC中,AB=8 m,AC=6 m,∠BAC=90°,试求小明家圆形花坛的面积.
(2)∵∠BAC=90°,AB=8 m,AC=6 m,
∴BC=10 m.
∴△ABC外接圆的半径为5 m,
∴小明家圆形花坛的面积为25π m2 .
8 m
6 m
10 m
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
点和圆的位置关系
点和圆的位置关系
三角形的外接圆
点P在圆外
点P在圆内
点P在圆上
d<r
d=r
d>r
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
外接圆圆心是三角形的三边的垂直平分线的交点,叫做这个三角形的外心.
布置作业
教科书第95页练习
第2、3题
第102页习题24.2
第2、9题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
24.2.1 点和圆的位置关系
第1课时
学习目标
1. 探索并掌握点和圆的位置关系,及这三种位置关系对应的圆的半径与点到圆心的距离之间的关系;
2. 了解三角形的外接圆和三角形的外心等概念;
3. 经历“不在同一直线上的三个点确定一个圆”的探索过程,培养学生的探索能力,进一步体会解决数学问题的策略;
4. 形成解决问题的一些基本策略,体验解决问题策略的多样性,发展实践能力与创新精神.
点和圆的位置关系
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察与思考
我国射击运动员在奥运会上屡获金牌,为我国赢得荣誉,图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
观察与思考
下图是一位射击运动员,六发子弹在射击靶上留下的痕迹.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察与思考
观察点和圆的位置关系,能否对这六个点进行分类?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
平面上的圆把平面分成了哪几部分?
圆内
圆外
圆上
思考
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察点和圆的位置关系,能否对这六个点进行分类?
B
C
A
D
E
F
点C、F在圆外
点A、D在圆内
点B、E在圆上
思考
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
设⊙O的半径为r,OA,OB,OC与r有怎样的数量关系?
B
C
A
O
思考
OA<r
OB r
OC>r
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
r
点P在圆外
点P在圆内
点P在圆上
归纳
设⊙O的半径为r,点P到圆心的距离OP=d
P
O
P
O
P
O
d<r
d=r
d>r
位置关系
数量关系
点和圆的位置关系
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
符号“ ”读作“等价于”,它表示从符号左端可以推出右端,从右端也可以推出左端.
现在知道击中靶上不同位置的成绩是如何计算的吗?
射击成绩用弹着点位置对应的环数表示.弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击成绩越好.
想一想
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知⊙O的面积为25π:
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上;
(4)若点P不在圆外,则PO .
做一做
5
圆外
圆内
≤5
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
回忆一下作一个圆需要哪些条件?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
r
已知圆心和半径,可以作一个圆
确定一个圆需要几个点呢
两点确定一条直线.
已知圆心和半径,可以作一个圆,经过一个已知点A能不能作圆,这样的圆你能作出多少个?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
可作无数个圆
…
思考
经过两个已知点A,B能不能作圆?如果能,圆心分布有什么特点?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
可作无数个圆
∵所作圆的圆心到A,B的距离相等
∴圆心在线段AB的垂直平分线上
B
A
思考
经过不在同一条直线上的三个点A,B,C能否作圆?如果能,如何确定所作圆的圆心?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
A
B
C
分组讨论:
1.学生先分组进行讨论;
2.教师根据讨论情况作相应提示;
3.学生讲解思路,教师补充完善.
经过不在同一条直线上的三个点A,B,C能否作圆?如果能,如何确定所作圆的圆心?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
A
B
C
所作圆经过A,B,C三点
圆心O到A,B,C三点距离相等
圆心O在线段AB的垂直平分线上
圆心O也在线段BC的垂直平分线上
圆心O为两线段垂直平分线的交点
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
A
B
C
作法:
(1)分别作出线段AB,BC的垂直平分线l1,l2;
(2)l1与l2交于点O,
(3)圆O即为所作圆.
O
不在同一条直线上的三个点确定一个圆
l1
l2
经过不在同一条直线上的三个点A,B,C能否作圆?如果能,如何确定所作圆的圆心?
以点O为圆心,OA的长为
半径作圆;
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
A
B
C
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
O
l1
l2
拓展
外接圆圆心是三角形的三边的垂直平分线的交点,叫做这个三角形的外心.
△ABC的外接圆
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1.如图,在△ABC中,∠C=90°,AB=5 cm,BC=4 cm,以A为圆心,以3 cm为半径画圆,请判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
解:在△ABC中,由勾股定理得:
(1)∵AC=3 cm,∴点C在⊙A上.
(2)∵AB=5 cm>3 cm,∴点B在⊙A外.
(3)∵点D是AB的中点,∴AD=2.5 cm<3 cm,∴点D在⊙A内.
创设情境
3 cm
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2.某地出土一明代残破圆形瓷盘,如图所示.为复制该瓷盘确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心.
(不要求写作法、证明和讨论,但要保留作图痕迹)
A
B
C
O
创设情境
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.两个圆心为O的甲、乙两圆,半径分别为r1和r2,且r1<OA<r2,那么点A在( )
A.甲圆内 B.乙圆外
C.甲圆外,乙圆内 D.甲圆内,乙圆外
2.如果⊙O的半径为r,点P到圆心O的距离为6,那么
①点P在⊙O外,则r ;
②点P在 ,则r=6;
③点P在 ,则r>6.
C
<6
⊙O上
⊙O内
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
(2)若在△ABC中,AB=8 m,AC=6 m,∠BAC=90°,试求小明家圆形花坛的面积.
解:(1)如图所示,⊙O即为所求作的花坛的位置.
O
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
(2)若在△ABC中,AB=8 m,AC=6 m,∠BAC=90°,试求小明家圆形花坛的面积.
(2)∵∠BAC=90°,AB=8 m,AC=6 m,
∴BC=10 m.
∴△ABC外接圆的半径为5 m,
∴小明家圆形花坛的面积为25π m2 .
8 m
6 m
10 m
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
点和圆的位置关系
点和圆的位置关系
三角形的外接圆
点P在圆外
点P在圆内
点P在圆上
d<r
d=r
d>r
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
外接圆圆心是三角形的三边的垂直平分线的交点,叫做这个三角形的外心.
布置作业
教科书第95页练习
第2、3题
第102页习题24.2
第2、9题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
