人教版九年级数学上册24.2.1点和圆的位置关系 (第2课时) 课件(共17张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.2.1点和圆的位置关系 (第2课时) 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
配套人教版
24.2.1 点和圆的位置关系
第2课时
学习目标
1.通过实例理解反证法的含义,并了解运用反证法证明的基本步骤;
2.通过反证法的证明过程,体会新的证明方法和思路;
3.在“分析、推理”等过程中,培养学生的推理能力以及逻辑思维能力;
4.利用现实生活和数学中的反证法素材体会“正难则反”的思想,开拓思维,并激发学生的求知、探索欲望.
反
证法
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
《世说新语》记载:王戎七岁,尝与诸小儿游.道边李树多子折枝,诸儿竞去取之,唯戎不动.人问之,答曰:“树在道边而多子,必苦李.”取之,信然.
王戎是怎么知道李子是苦的呢?
大家谈谈
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
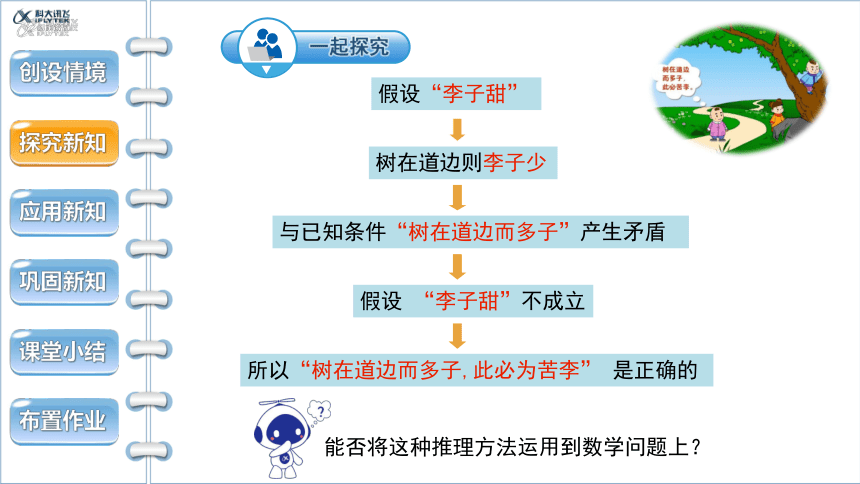
一起探究
假设“李子甜”
树在道边则李子少
与已知条件“树在道边而多子”产生矛盾
假设 “李子甜”不成立
所以“树在道边而多子,此必为苦李” 是正确的
能否将这种推理方法运用到数学问题上?
经过同一条直线上的三个点能作出一个圆吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
证明猜想
l1
l2
A
B
C
P
l
已知:点A、 B、 C三点在直线l上
求证:过A、 B、 C三点不能作圆
证明:假设经过同一条直线l上的A、B、C三点可以作一个圆.
设这个圆的圆心为P,
那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,
即点P为l1与l2的交点,
而l1⊥l,l2⊥l,这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,
所以,经过同一条直线上的三个点不能作圆.
假设命题不成立
推出矛盾
原命题成立
不在同一直线上的三个点确定一个圆.
归纳
在证明一个命题时,先假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.这种方法叫做反证法.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
定义
与以前学过的证明不同
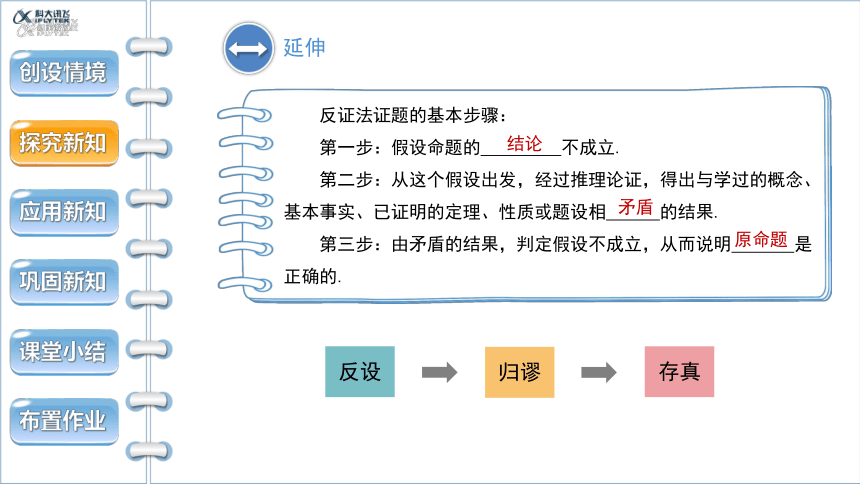
反证法证题的基本步骤:
第一步:假设命题的 不成立.
第二步:从这个假设出发,经过推理论证,得出与学过的概念、
基本事实、已证明的定理、性质或题设相 的结果.
第三步:由矛盾的结果,判定假设不成立,从而说明 是
正确的.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
延伸
结论
矛盾
原命题
反设
归谬
存真
什么样的命题适合用反证法证明呢?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
延伸
正难则反
直接证明有困难
否定性命题
唯一性命题
至多、至少型命题
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
延伸
反证法是数学家最精良的武器之一.
——牛顿
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
【例】用反证法证明:两直线平行,同位角相等.
分组讨论:
1.学生先分组进行讨论;
2.学生讲解思路;
3.教师补充完善.
创设情境
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
证明:假设∠1≠∠2,过点O作直线A′B′,使∠EOB′=∠2.
根据“同位角相等,两直线平行”,可得A′B′∥CD,这样,
过点O就有两条直线AB ,A′B′都平行于CD,这与平行公理
“过直线外一点有且仅有一条直线与已知直线平行”矛盾.
这说明∠1≠∠2不正确,所以∠1=∠2.
已知:如图,AB∥CD,直线EF交AB于点O,
求证:∠1=∠2.
B′
F
E
A
A′
O
B
C
D
1
2
反设
归谬
存真
创设情境
【例】用反证法证明:两直线平行,同位角相等.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.试说出下列命题的反面:
(1)a是实数. (2)a大于2.
(3)a小于2. (4)至少有2个.
(5)至少有一个. (6)两条直线平行.
2.用反证法证明“若a2≠ b2,则a ≠ b”的第一步是 .
a不是实数
a小于等于2
最多有一个
一个也没有
两条直线不平行
a大于等于2
假设a=b
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.在△ABC中,AB≠AC,求证:∠B≠∠C.
证明:假设 ,
则 ( )
这与 矛盾.
假设不成立.
∴ .
A
B
C
∠B=∠C
AB=AC
等角对等边
已知AB≠AC
∠B≠∠C
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
4.求证:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
已知:如图,l1∥l2 ,l2∥l3
求证:l1∥l3
证明:假设l1不平行l3,则l1与l3相交,设交点为P.
∵l1∥l2 ,l2∥l3, 则过点P就有两条直线l1、 l3都与l2平行,这与“经过直线外一点,有且只有一条直线平行于已知直线”矛盾.所以假设不成立,原命题结论成立,
即 l1∥l3 .
l2
l1
l3
P
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
反证法
反证法的概念
反证法的步骤
在证明一个命题时,先假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.这种方法叫做反证法.
反设
归谬
存真
布置作业
复习巩固
教科书第94页内容
举出两个数学中能用反证法证明的例子.
探究新知
应用新知
课堂小结
巩固新知
创设情境
配套人教版
再见
配套人教版
24.2.1 点和圆的位置关系
第2课时
学习目标
1.通过实例理解反证法的含义,并了解运用反证法证明的基本步骤;
2.通过反证法的证明过程,体会新的证明方法和思路;
3.在“分析、推理”等过程中,培养学生的推理能力以及逻辑思维能力;
4.利用现实生活和数学中的反证法素材体会“正难则反”的思想,开拓思维,并激发学生的求知、探索欲望.
反
证法
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
《世说新语》记载:王戎七岁,尝与诸小儿游.道边李树多子折枝,诸儿竞去取之,唯戎不动.人问之,答曰:“树在道边而多子,必苦李.”取之,信然.
王戎是怎么知道李子是苦的呢?
大家谈谈
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
一起探究
假设“李子甜”
树在道边则李子少
与已知条件“树在道边而多子”产生矛盾
假设 “李子甜”不成立
所以“树在道边而多子,此必为苦李” 是正确的
能否将这种推理方法运用到数学问题上?
经过同一条直线上的三个点能作出一个圆吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
证明猜想
l1
l2
A
B
C
P
l
已知:点A、 B、 C三点在直线l上
求证:过A、 B、 C三点不能作圆
证明:假设经过同一条直线l上的A、B、C三点可以作一个圆.
设这个圆的圆心为P,
那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,
即点P为l1与l2的交点,
而l1⊥l,l2⊥l,这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,
所以,经过同一条直线上的三个点不能作圆.
假设命题不成立
推出矛盾
原命题成立
不在同一直线上的三个点确定一个圆.
归纳
在证明一个命题时,先假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.这种方法叫做反证法.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
定义
与以前学过的证明不同
反证法证题的基本步骤:
第一步:假设命题的 不成立.
第二步:从这个假设出发,经过推理论证,得出与学过的概念、
基本事实、已证明的定理、性质或题设相 的结果.
第三步:由矛盾的结果,判定假设不成立,从而说明 是
正确的.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
延伸
结论
矛盾
原命题
反设
归谬
存真
什么样的命题适合用反证法证明呢?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
延伸
正难则反
直接证明有困难
否定性命题
唯一性命题
至多、至少型命题
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
延伸
反证法是数学家最精良的武器之一.
——牛顿
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
【例】用反证法证明:两直线平行,同位角相等.
分组讨论:
1.学生先分组进行讨论;
2.学生讲解思路;
3.教师补充完善.
创设情境
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
证明:假设∠1≠∠2,过点O作直线A′B′,使∠EOB′=∠2.
根据“同位角相等,两直线平行”,可得A′B′∥CD,这样,
过点O就有两条直线AB ,A′B′都平行于CD,这与平行公理
“过直线外一点有且仅有一条直线与已知直线平行”矛盾.
这说明∠1≠∠2不正确,所以∠1=∠2.
已知:如图,AB∥CD,直线EF交AB于点O,
求证:∠1=∠2.
B′
F
E
A
A′
O
B
C
D
1
2
反设
归谬
存真
创设情境
【例】用反证法证明:两直线平行,同位角相等.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.试说出下列命题的反面:
(1)a是实数. (2)a大于2.
(3)a小于2. (4)至少有2个.
(5)至少有一个. (6)两条直线平行.
2.用反证法证明“若a2≠ b2,则a ≠ b”的第一步是 .
a不是实数
a小于等于2
最多有一个
一个也没有
两条直线不平行
a大于等于2
假设a=b
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.在△ABC中,AB≠AC,求证:∠B≠∠C.
证明:假设 ,
则 ( )
这与 矛盾.
假设不成立.
∴ .
A
B
C
∠B=∠C
AB=AC
等角对等边
已知AB≠AC
∠B≠∠C
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
4.求证:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
已知:如图,l1∥l2 ,l2∥l3
求证:l1∥l3
证明:假设l1不平行l3,则l1与l3相交,设交点为P.
∵l1∥l2 ,l2∥l3, 则过点P就有两条直线l1、 l3都与l2平行,这与“经过直线外一点,有且只有一条直线平行于已知直线”矛盾.所以假设不成立,原命题结论成立,
即 l1∥l3 .
l2
l1
l3
P
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
反证法
反证法的概念
反证法的步骤
在证明一个命题时,先假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.这种方法叫做反证法.
反设
归谬
存真
布置作业
复习巩固
教科书第94页内容
举出两个数学中能用反证法证明的例子.
探究新知
应用新知
课堂小结
巩固新知
创设情境
配套人教版
再见
同课章节目录
