人教版九年级数学上册22.1.1二次函数 课件(共18张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.1.1二次函数 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 646.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 20:57:26 | ||
图片预览






文档简介
(共18张PPT)
第二十二章 二次函数
二次函数的图像和性质
第 1 课时
1. 一元二次方程的一般形式是什么?
2. 函数定义是什么?
设在一个变化过程中有两个变量 x 与 y ,如果对于 x 的每一个值, y 都有唯一的值与它对应,那么就说 x 是自变量, y 是 x 的函数.
3. 一次函数,正比例函数的一般形式是什么?
一次函数:y = kx+b(k , b 是常数,k ≠ 0)
正比例函数:y = kx(k 是常数,k ≠ 0)
一、复习回顾
1. 现有一根 12 m 长的绳子,用它围成一个矩形,如何围法,才使举行的面积最大?小明同学认为当围成的矩形是正方形时 ,它的面积最大,他说的有道理吗?
2. 很多同学都喜欢打篮球,你知道吗:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
这些问题都可以通过学习二次函数的数学模型来解决
二、合作交流,探究新知
请用适当的函数解析式表示下列问题情境中的两个变量 y 与 x 之间的关系:
(1) 圆的面积 y ( cm2 )与圆的半径 x ( cm )
y = πx2
(2) 某商店 1 月份的利润是 2 万元,2、3 月份利润逐月增长,这两个月利润的月平均增长率为 x,3月份的利润为 y
y = 2(1+x)2
二、合作交流,探究新知
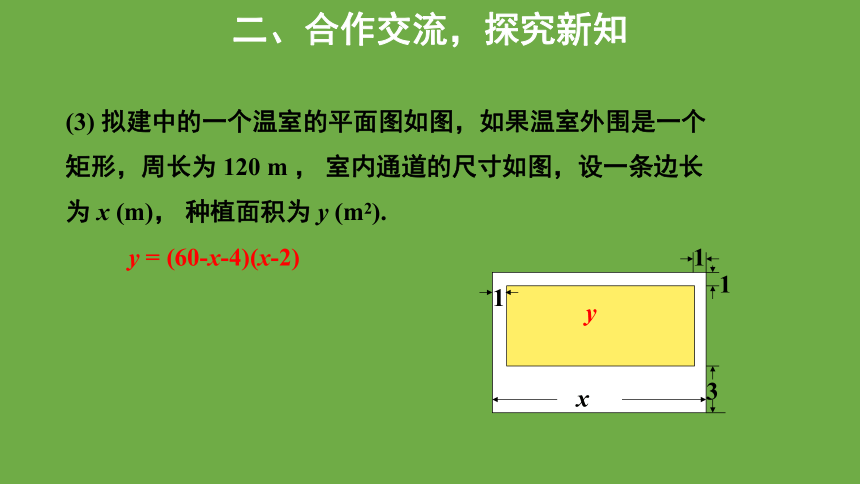
(3) 拟建中的一个温室的平面图如图,如果温室外围是一个矩形,周长为 120 m , 室内通道的尺寸如图,设一条边长为 x (m), 种植面积为 y (m2).
y = (60-x-4)(x-2)
1
1
1
3
x
y
二、合作交流,探究新知
y = πx2
y = 2(1+x)2 = 2x2+4x+2
y = (60-x-4)(x-2) = -x2+58x-112
y 是 x 的函数吗?y 是 x 的一次函数?反比例函数?
上述三个问题中的函数解析式具有哪些共同的特征?
在上面的问题中,函数都是用自变量的二次式表示的,
经化简后都具有 y=ax +bx+c 的形式.
(a,b,c 是常数,a ≠ 0 )
二、合作交流,探究新知
定义:一般地,形如 y = ax +bx+c ( a,b,c 是常数,a ≠ 0)的函数叫做 x 的二次函数.
注意:
(1)等号左边是变量 y,右边是关于自变量 x 的整式.
(2)a,b,c为常数,且 a ≠ 0.
(3 )等式的右边最高次数为 2 ,可以没有一次项和常数项,但不能没有二次项.
(4)x 的取值范围通常情况是任意实数.
二、合作交流,探究新知
二次函数的一般形式:
y= ax2+bx+c (其中a、b、c是常数,a ≠ 0 )
a 是二次项系数, b 是一次项系数, c 是常数项
二次函数的特殊形式:
当 b=0 时, y=ax2+c
当 c=0 时, y=ax2+bx
当 b=0,c=0 时, y=ax2
二、合作交流,探究新知
1. 已知二次函数 y=x2+px+q ,当 x=1 时,函数值是 4;当 x=2 时,函数值是 -5 ,求这个二次函数的解析式.
解:以 x=1、y=4 代入,得:
p+q+1=4 , 即:p+q=3 (1)
以 x=2、y=-5 代入,得:
4+2p+q=-5 ,即:2p+q=-9 (2)
解(1)、(2),得:
p=-12、q=15
则:y=x -12x+15
三、运用新知
2. 如图,一张正方形纸板的边长为 2 cm,将它剪去 4 个全等的直角三角形 (图中阴影部分 ) ,设AE = BF = CG = DH = x (cm),四边形 EFGH 的面积为 y (cm2) ,求 :
(1) 求 y 关于 x 的函数解析式和自变量 x 的取值范围
(2) 当 x 分别为 0.25,0.5,1,1.5,
1.75 时 ,求对应的四边形EFGH的
面积 y,并列表表示.
(3) 随着 x 的取值的增大,y 的值有怎样的变化?
三、运用新知
解:(1)∵在正方形纸上剪去 4 个全等的直角三角形,
∴∠AHE=∠DGH,∠DGH+∠DHG=90°,HG=HE,
∵∠EHG=180°-∠AHE-∠DHG,
∴∠EHG=90°,四边形EFGH为正方形,
在△AEH中,AE=x,AH=BE=AB-AE=2-x,∠A=90°,
∴HE2=AE2+AH2=x2+(2-x)2=2x2-4x+4,
正方形EFGH的面积y=HE2=2x2-4x+4,
∵AE,AH不能为负,∴0≤x≤2,
故y关于x的函数表达式:y=2x2-4x+4,自变量 x 的取值范围0≤x≤2。
三、运用新知
解:(2)
(3)由上表可以看出:
随着 x 的取值的增大,y 的值先减小后增大.
x 0.25 0.5 1 1.5 1.75
y
三、运用新知
1. 下列函数中,哪些是二次函数
是
不是
是
不是
四、巩固新知
2.若函数 为二次函数,求 m 的值.
解:因为该函数为二次函数,
则
解得:m = 2
注意:二次函数的二次项系数不能为零.
四、巩固新知
3. 要用长 20 m 的铁栏杆,一面靠墙,围成一个矩形的花圃,设连墙的一边为 x ,巨形的面积为 y ,求:
(1)写出 y 关与 x 的函数关系式.
(2)当 x = 3 时,距形的面积为多少
解:(1) y = x(20-2x)
= -2x2+20x (0(2)y = -2×32+20×3 = 42m2
x
四、巩固新知
1. 定义:一般地,形如 y=ax +bx+c (a,b,c是常数,a ≠ 0)的函数叫做 x 的二次函数.
2. 定义的实质是:ax2+bx+c 是整式,自变量 x 的最高次是二次,自变量 x 的取值范围是全体实数.
3. 二次函数的一般形式:
y=ax2+bx+c (其中 a、b、c 是常数,a ≠0 )
a 是二次项系数, b 是一次项系数, c 是常数项
五、归纳小结
二次函数的特殊形式:
当 b=0 时, y=ax2+c
当 c=0 时, y=ax2+bx
当 b=0,c=0时, y=ax2
五、归纳小结
再见
第二十二章 二次函数
二次函数的图像和性质
第 1 课时
1. 一元二次方程的一般形式是什么?
2. 函数定义是什么?
设在一个变化过程中有两个变量 x 与 y ,如果对于 x 的每一个值, y 都有唯一的值与它对应,那么就说 x 是自变量, y 是 x 的函数.
3. 一次函数,正比例函数的一般形式是什么?
一次函数:y = kx+b(k , b 是常数,k ≠ 0)
正比例函数:y = kx(k 是常数,k ≠ 0)
一、复习回顾
1. 现有一根 12 m 长的绳子,用它围成一个矩形,如何围法,才使举行的面积最大?小明同学认为当围成的矩形是正方形时 ,它的面积最大,他说的有道理吗?
2. 很多同学都喜欢打篮球,你知道吗:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
这些问题都可以通过学习二次函数的数学模型来解决
二、合作交流,探究新知
请用适当的函数解析式表示下列问题情境中的两个变量 y 与 x 之间的关系:
(1) 圆的面积 y ( cm2 )与圆的半径 x ( cm )
y = πx2
(2) 某商店 1 月份的利润是 2 万元,2、3 月份利润逐月增长,这两个月利润的月平均增长率为 x,3月份的利润为 y
y = 2(1+x)2
二、合作交流,探究新知
(3) 拟建中的一个温室的平面图如图,如果温室外围是一个矩形,周长为 120 m , 室内通道的尺寸如图,设一条边长为 x (m), 种植面积为 y (m2).
y = (60-x-4)(x-2)
1
1
1
3
x
y
二、合作交流,探究新知
y = πx2
y = 2(1+x)2 = 2x2+4x+2
y = (60-x-4)(x-2) = -x2+58x-112
y 是 x 的函数吗?y 是 x 的一次函数?反比例函数?
上述三个问题中的函数解析式具有哪些共同的特征?
在上面的问题中,函数都是用自变量的二次式表示的,
经化简后都具有 y=ax +bx+c 的形式.
(a,b,c 是常数,a ≠ 0 )
二、合作交流,探究新知
定义:一般地,形如 y = ax +bx+c ( a,b,c 是常数,a ≠ 0)的函数叫做 x 的二次函数.
注意:
(1)等号左边是变量 y,右边是关于自变量 x 的整式.
(2)a,b,c为常数,且 a ≠ 0.
(3 )等式的右边最高次数为 2 ,可以没有一次项和常数项,但不能没有二次项.
(4)x 的取值范围通常情况是任意实数.
二、合作交流,探究新知
二次函数的一般形式:
y= ax2+bx+c (其中a、b、c是常数,a ≠ 0 )
a 是二次项系数, b 是一次项系数, c 是常数项
二次函数的特殊形式:
当 b=0 时, y=ax2+c
当 c=0 时, y=ax2+bx
当 b=0,c=0 时, y=ax2
二、合作交流,探究新知
1. 已知二次函数 y=x2+px+q ,当 x=1 时,函数值是 4;当 x=2 时,函数值是 -5 ,求这个二次函数的解析式.
解:以 x=1、y=4 代入,得:
p+q+1=4 , 即:p+q=3 (1)
以 x=2、y=-5 代入,得:
4+2p+q=-5 ,即:2p+q=-9 (2)
解(1)、(2),得:
p=-12、q=15
则:y=x -12x+15
三、运用新知
2. 如图,一张正方形纸板的边长为 2 cm,将它剪去 4 个全等的直角三角形 (图中阴影部分 ) ,设AE = BF = CG = DH = x (cm),四边形 EFGH 的面积为 y (cm2) ,求 :
(1) 求 y 关于 x 的函数解析式和自变量 x 的取值范围
(2) 当 x 分别为 0.25,0.5,1,1.5,
1.75 时 ,求对应的四边形EFGH的
面积 y,并列表表示.
(3) 随着 x 的取值的增大,y 的值有怎样的变化?
三、运用新知
解:(1)∵在正方形纸上剪去 4 个全等的直角三角形,
∴∠AHE=∠DGH,∠DGH+∠DHG=90°,HG=HE,
∵∠EHG=180°-∠AHE-∠DHG,
∴∠EHG=90°,四边形EFGH为正方形,
在△AEH中,AE=x,AH=BE=AB-AE=2-x,∠A=90°,
∴HE2=AE2+AH2=x2+(2-x)2=2x2-4x+4,
正方形EFGH的面积y=HE2=2x2-4x+4,
∵AE,AH不能为负,∴0≤x≤2,
故y关于x的函数表达式:y=2x2-4x+4,自变量 x 的取值范围0≤x≤2。
三、运用新知
解:(2)
(3)由上表可以看出:
随着 x 的取值的增大,y 的值先减小后增大.
x 0.25 0.5 1 1.5 1.75
y
三、运用新知
1. 下列函数中,哪些是二次函数
是
不是
是
不是
四、巩固新知
2.若函数 为二次函数,求 m 的值.
解:因为该函数为二次函数,
则
解得:m = 2
注意:二次函数的二次项系数不能为零.
四、巩固新知
3. 要用长 20 m 的铁栏杆,一面靠墙,围成一个矩形的花圃,设连墙的一边为 x ,巨形的面积为 y ,求:
(1)写出 y 关与 x 的函数关系式.
(2)当 x = 3 时,距形的面积为多少
解:(1) y = x(20-2x)
= -2x2+20x (0
x
四、巩固新知
1. 定义:一般地,形如 y=ax +bx+c (a,b,c是常数,a ≠ 0)的函数叫做 x 的二次函数.
2. 定义的实质是:ax2+bx+c 是整式,自变量 x 的最高次是二次,自变量 x 的取值范围是全体实数.
3. 二次函数的一般形式:
y=ax2+bx+c (其中 a、b、c 是常数,a ≠0 )
a 是二次项系数, b 是一次项系数, c 是常数项
五、归纳小结
二次函数的特殊形式:
当 b=0 时, y=ax2+c
当 c=0 时, y=ax2+bx
当 b=0,c=0时, y=ax2
五、归纳小结
再见
同课章节目录
