人教版六年级下册数学《不规则物体体积的计算》课件(共22张PPT)
文档属性
| 名称 | 人教版六年级下册数学《不规则物体体积的计算》课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 06:33:35 | ||
图片预览





文档简介
(共22张PPT)
六年级下册
不规则物体体积计算
人教版六年级数学下册《圆柱与圆锥》P26例7
输入标题
学习目标
在解决问题的过程中体会转化、推理和变中有不变的数学思想。
经历发现和提出问题、分析和解决问题的完整过程,培养观察、概括的能力。
准备好了吗?一起去探索吧!
不规则物体体积计算
通过观察比较,掌握不规则物体的体积的计算方法,熟练运用圆柱的体积计算公式解决实际问题。
净含量:550ml
告诉我们什么?
商家标注存在虚假吗?我们可以怎样验证?
合作探究
1、你能直接通过测量相关数据计算出水部分的体积吗?为什么?小组里动手试试吧!再独立进行计算。(数据用去尾法保留整数)
2、你能直接通过测量相关数据计算出空气部分的体积吗?为什么?小组里也动手试试吧!再独立进行计算。 (数据用去尾法保留整数)
3、怎样计算你手中水瓶的容积?是多少毫升?商家的标识存在虚假吗?
go 5
go 7
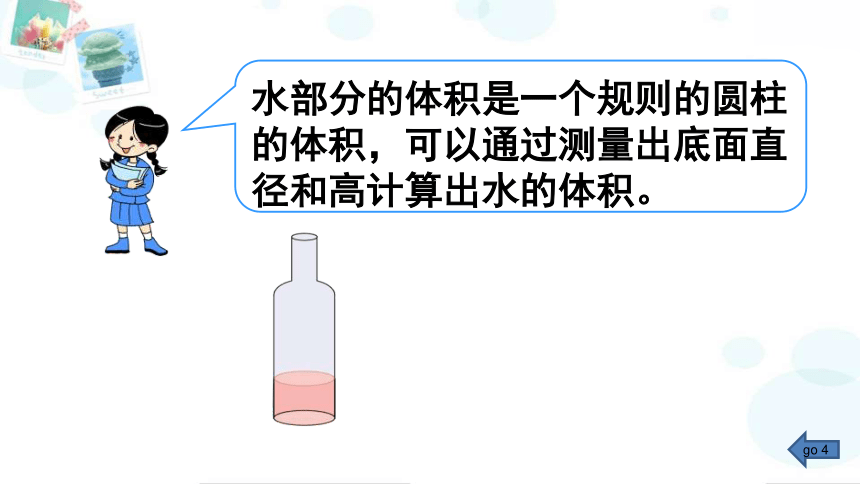
水部分的体积是一个规则的圆柱的体积,可以通过测量出底面直径和高计算出水的体积。
go 4
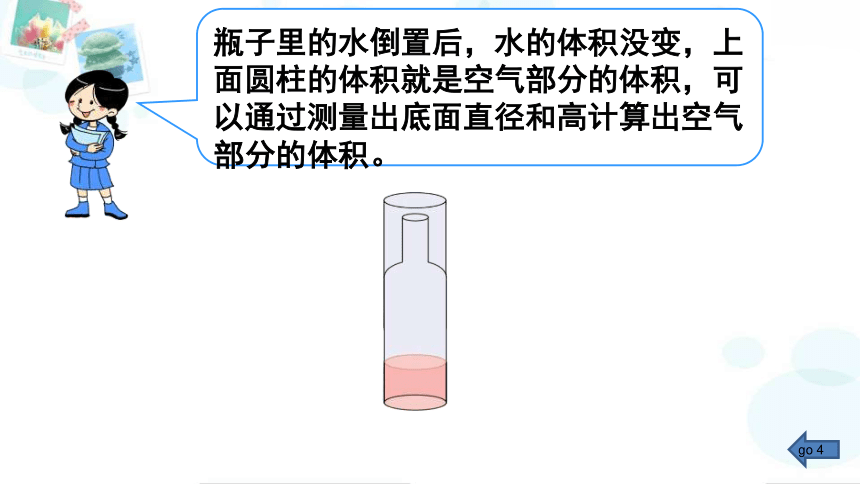
瓶子里的水倒置后,水的体积没变,上面圆柱的体积就是空气部分的体积,可以通过测量出底面直径和高计算出空气部分的体积。
go 4
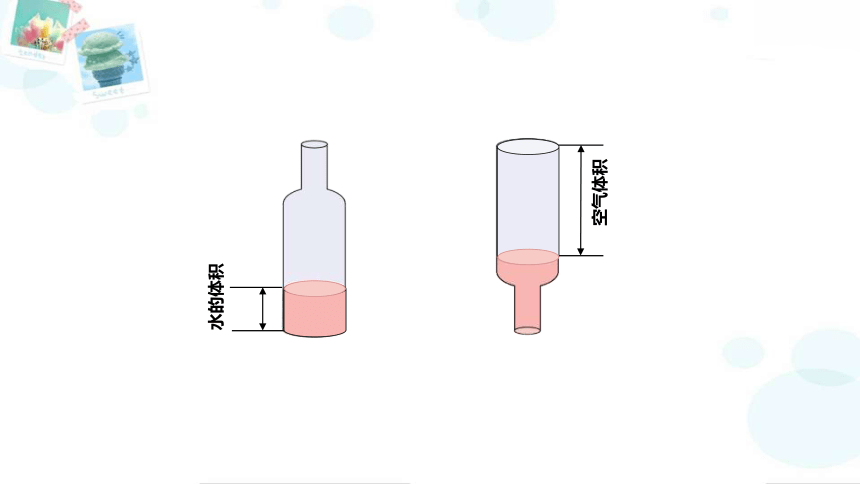
水的体积
空气体积
上面计算水瓶的容积时,我们用到了转化的方法。将不规则空气部分的体积转化成规则的圆柱,
也就是把不规则的水瓶转化成规则的圆柱。
等积变形
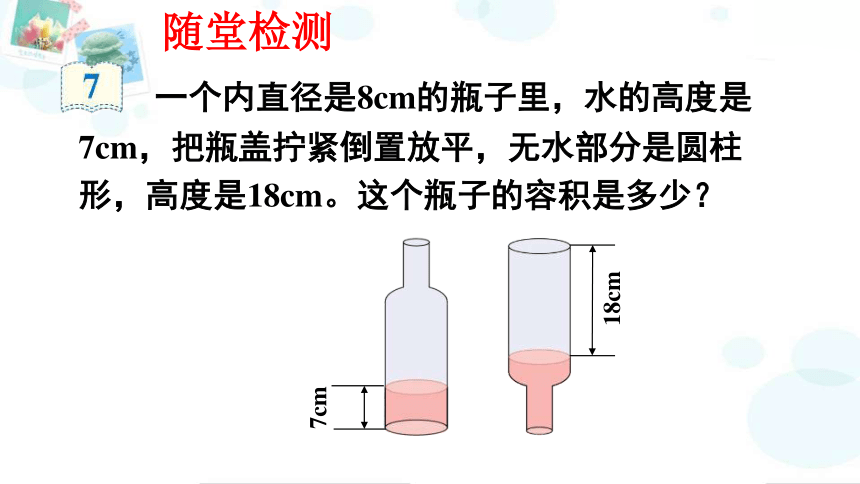
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
7cm
18cm
随堂检测
7cm
瓶子的容积转化成两个圆柱的体积。
18cm
答:这个瓶子的容积是1256mL。
瓶子的容积:
3.14×(8÷2)2×7+3.14×(8÷2)2×18
=3.14×16×(7+18)
=3.14×16×25
=1256 (cm )
=1256(mL)
图1中的空气与图2中的空气体积相等,把图2中的空气换到图1上,如下图,就能形成一个规则的圆柱。
思
考
你还能想到别的方法吗?
7cm
18cm
1
2
7cm
18cm
1
2
7cm
18cm
瓶子的容积:
3.14×(8÷2)2×(7+18)
=3.14×16×25
=1256 (cm )
=1256(mL)
你能计算出这个石块的体积的吗?
随堂检测
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
10cm
随堂检测
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(cm )
=282.6(mL)
10cm
一个输液瓶中装有100mL药液,每分钟输2.5mL,下面是12分钟后输液瓶内剩余的药液,请你求出整个输液瓶的容积。
2.5×12=30(mL)
100-30+80=150(mL)
答:整个输液瓶的容积是150mL。
能力提升
有一饮料瓶的容积是1.5升,现在它里面装有一些饮料,正放时饮料高度是15厘米,倒放时空余部分高度为5厘米,问瓶内现有饮料多少升?
能力提升
1.5升=1500立方厘米
1500÷(15+5)=75(平方厘米)
75×15=1125(立方厘米)=1.125(升)
答:瓶内现有饮料1.125升。
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
我们学习了什么
规则物体
不规则物体
转化
形状变了
体积不变
等积变形
1.完成P28第9—12题;
2.完成练习册本课时的习题。
课后练习
六年级下册
不规则物体体积计算
人教版六年级数学下册《圆柱与圆锥》P26例7
输入标题
学习目标
在解决问题的过程中体会转化、推理和变中有不变的数学思想。
经历发现和提出问题、分析和解决问题的完整过程,培养观察、概括的能力。
准备好了吗?一起去探索吧!
不规则物体体积计算
通过观察比较,掌握不规则物体的体积的计算方法,熟练运用圆柱的体积计算公式解决实际问题。
净含量:550ml
告诉我们什么?
商家标注存在虚假吗?我们可以怎样验证?
合作探究
1、你能直接通过测量相关数据计算出水部分的体积吗?为什么?小组里动手试试吧!再独立进行计算。(数据用去尾法保留整数)
2、你能直接通过测量相关数据计算出空气部分的体积吗?为什么?小组里也动手试试吧!再独立进行计算。 (数据用去尾法保留整数)
3、怎样计算你手中水瓶的容积?是多少毫升?商家的标识存在虚假吗?
go 5
go 7
水部分的体积是一个规则的圆柱的体积,可以通过测量出底面直径和高计算出水的体积。
go 4
瓶子里的水倒置后,水的体积没变,上面圆柱的体积就是空气部分的体积,可以通过测量出底面直径和高计算出空气部分的体积。
go 4
水的体积
空气体积
上面计算水瓶的容积时,我们用到了转化的方法。将不规则空气部分的体积转化成规则的圆柱,
也就是把不规则的水瓶转化成规则的圆柱。
等积变形
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
7cm
18cm
随堂检测
7cm
瓶子的容积转化成两个圆柱的体积。
18cm
答:这个瓶子的容积是1256mL。
瓶子的容积:
3.14×(8÷2)2×7+3.14×(8÷2)2×18
=3.14×16×(7+18)
=3.14×16×25
=1256 (cm )
=1256(mL)
图1中的空气与图2中的空气体积相等,把图2中的空气换到图1上,如下图,就能形成一个规则的圆柱。
思
考
你还能想到别的方法吗?
7cm
18cm
1
2
7cm
18cm
1
2
7cm
18cm
瓶子的容积:
3.14×(8÷2)2×(7+18)
=3.14×16×25
=1256 (cm )
=1256(mL)
你能计算出这个石块的体积的吗?
随堂检测
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
10cm
随堂检测
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(cm )
=282.6(mL)
10cm
一个输液瓶中装有100mL药液,每分钟输2.5mL,下面是12分钟后输液瓶内剩余的药液,请你求出整个输液瓶的容积。
2.5×12=30(mL)
100-30+80=150(mL)
答:整个输液瓶的容积是150mL。
能力提升
有一饮料瓶的容积是1.5升,现在它里面装有一些饮料,正放时饮料高度是15厘米,倒放时空余部分高度为5厘米,问瓶内现有饮料多少升?
能力提升
1.5升=1500立方厘米
1500÷(15+5)=75(平方厘米)
75×15=1125(立方厘米)=1.125(升)
答:瓶内现有饮料1.125升。
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
我们学习了什么
规则物体
不规则物体
转化
形状变了
体积不变
等积变形
1.完成P28第9—12题;
2.完成练习册本课时的习题。
课后练习
