数学人教A版(2019)必修第二册8.4.1平面 课件(共32张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.4.1平面 课件(共32张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 26.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 05:28:01 | ||
图片预览










文档简介
(共32张PPT)
第8章
8.4.1 平面
CONTENTS
目录
基本事实二
2
基本事实一
1
基本事实三
3
基本事实一
1
一、观察生活中的平面
桌面
海平面
黑板平面
桌面,海平面,都是水平放置平面
黑板平面,墙面,是竖直放置平面
二、平面的概念和画法
1、水平放置平面:
(1)通常用平行四边形表示平面
(2)水平边长画成邻边长的2倍
(3)锐角画成45°
平面的概念:
数学中的平面是指平坦、光滑、并且可以无限延展的图形。
平面的画法:
2、竖直放置平面:
(1)通常用平行四边形表示平面
(2)竖直边长画成邻边长的2倍
(3)锐角画成45°
平面
的表示
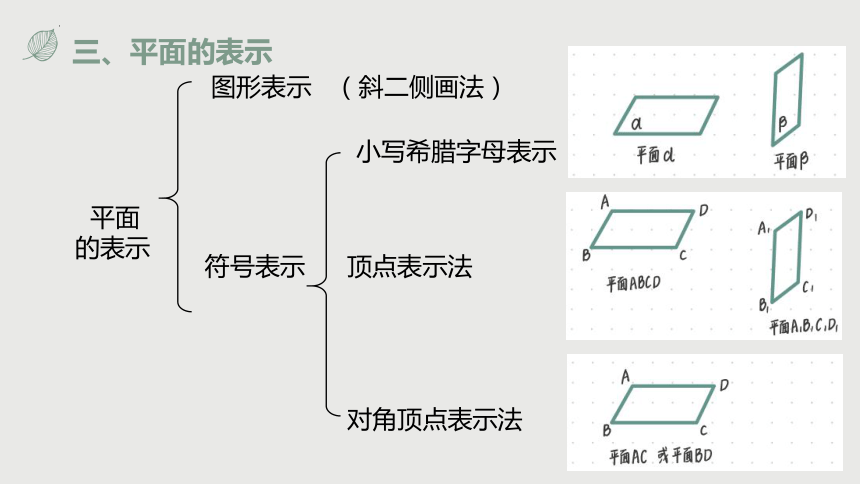
图形表示 (斜二侧画法)
符号表示
小写希腊字母表示
对角顶点表示法
顶点表示法
三、平面的表示
四、实验探索
小组合作:
分别用一个指尖、两个指尖、三个指尖表示点。用一个本子表示一个平面。看看几个指尖能平稳地将本子顶起来?
?
那么几个点能确定一个平面呢
我们知道:两点确定一条直线。
五、生活实例
?
那么几个点能确定一个平面呢
三脚架有与地面有三个接触点
(三个交点不在同一条直线上)
自行车有与地面有三个接触点
(三个交点不在同一条直线上)
通过实验观察,我们发现:
只有当三个指尖不在同一条直线上时,本子能被平稳地顶起来。
公理一:过不在一条直线上的三个点,有且只有一个平面。
简称:“不共线的三点,确定一个平面”。
α
A
C
B
图形语言:
符号语言:
A、B、C、三点不共线
有且只有一个 平面α
使得A∈α,B∈α,C∈α
六、基本事实1
一、多选题:
下列说法正确的是( )
A、 经过一点,有无数个平面
B、 经过两点,无法确定一个平面
C、 经过三点,有且只有三个平面
D、 不共线的三点确定一个平面
E、 过不在同一条直线上的三个点,
有且只有一个平面
七、例题讲解
例题解析:
A、正确。经过一个点,有无数个平面
B、正确。经过两个点,有无数个平面。所以,两点无法确定一个平面。
C、错误。
如果三点共线,那么经过这三个点,有无数个平面。
如果三点不共线,那么经过这三个点,有且只有一个平面。(公理一)
D、正确。公理一:“不共线的三点确定一个平面”。
E、正确。公理一:过不在同一条直线上的三个点,有且只有一个平面。
ABDE
√
√
√
√
×
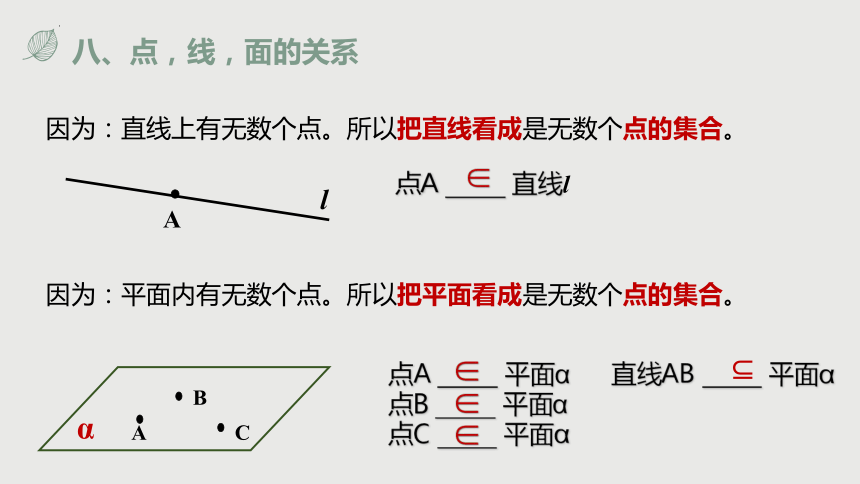
因为:直线上有无数个点。所以把直线看成是无数个点的集合。
α
A
C
B
八、点,线,面的关系
A
l
点A 直线l
∈
因为:平面内有无数个点。所以把平面看成是无数个点的集合。
点A 平面α
点B 平面α
点C 平面α
直线AB 平面α
∈
∈
∈
一、单选题:
下列说法正确的是( )
A、经过一点,有且只有一个平面
B、经过两点,有且只有两个平面
C、经过三点,有且只有一个平面
D、经过不共线的三个点,
有且只有一个平面
二、填空题:
1、
经过共线的三点,有 平面。
不共线的三点可确定 平面。
2、如图:
A 平面α; BC 平面α。
α
A
C
B
D
无数个
1个
∈
九、课堂练习
基本事实二
2
师生合作:取出一根木棍。
(1)当木棍与桌面没有任何交点时。木棍与桌面有什么位置关系?
(2)将木棍上任意一点,固定在桌面上。木棍与桌面有什么位置关系?
(3)将木棍上任意两点,固定在桌面上。木棍与桌面有什么位置关系?
(2)
(3)
(1)
一、实验探索
线与面的位置关系 图象语言
文字语言
交点个数
直线a//平面α
直线a不在平面α内
直线a在平面α内
0个
1个
无数个
二、得出结论
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内。
当一条直线上的所有点都在平面内时,称直线在平面内,或平面经过直线。
图形语言:
符号语言:
α
A
B
A∈直线
B∈直线
A∈平面α
B∈平面α
直线 平面α
三、基本事实2
线与面的位置关系 图象语言
文字语言
符号语言
直线a//平面α
直线a不在平面α内
直线a在平面α内
a 平面α
四、得出结论
a 平面α
a 平面α
α
推论1
经过一条直线和该直线外一点, 平面
符号语言:
A 有且只有一个平面α,使得A∈平面α, 平面α
A
有且只有 1个
五、推论1
α
推论2
经过两条相交直线, 平面
符号语言:
1 ∩ 2=A 有且只有一个平面α,使得 1 平面α, 2 平面α
1
2
A
有且只有 1个
五、推论2
推论3
经过两条平行直线, 平面
α
1
2
符号语言:
1// 2 有且只有一个平面α,使得 1 平面α, 2 平面α
有且只有1个
五、推论3
一、判断题:
1、一条直线上有两个点在一个平面内,那么这条直线在平面内( )
2、一条直线上有两个点在一个平面内,那么这个平面经过这条直线。( )
3、平面内的任意两条直线,无法确定一个平面( )
4、经过一条直线和直线上一点,有且只有一个平面。( )
5、经过一条直线和直线外一点,有且只有一个平面。( )
答案解析:
1、正确。公理二:如果一条直线上有两个点在一个平面内,那么这条直线上的所有点都在这个平面内。
2、正确。当一条直线上的所有点都在平面内时,称直线在平面内,或平面经过直线。
3、错误。平面内的两条直线,要么平行,要么相交。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
4、错误
5、正确
推论1:经过一条直线和该直线外一点,有且只有一个平面。
√
√
×
√
×
六、课堂练习
基本事实三
3
思考:把三角板的一个角立在桌面上。三角板所在的平面与桌面是否只交于一点P?为什么?对此你有什么结论?
α
β
因为平面具有无限延展性。所以三角板所在的平面β与桌面α,相交于直线 。
由此,得到基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条经过该点的公共直线。
此时称两个平面相交。公共直线称为两个平面的交线。
P
符号语言:
P∈α,P∈β 有且只有一条直线 ,使得P∈ ,α∩β=
一、基本事实3
一、作图题:
试用符号语言表示下列语句,并画出相应的图形。
(1)点A、点B在直线 上,直线 在平面α内。
(2)平面α和平面β相交于直线 。
α
A
B
(1)
(2)
α
β
注意:
画两个平面相交时,一定要画出它们的交线。平面被遮挡部分用虚线表示或不画。
二、课堂练习
一、选择题
2、两个平面相交,那么它们有( )
A. 零个公共交点
B. 一个公共交点
C. 两个公共交点
D. 无数个公共交点
α
β
二、看图填空
A
A 平面α; A 平面β
B 平面α; B 平面β
平面α∩平面β= 。
二、课堂练习
B
D
∈
∈
∈
∈
AB
课堂小结
4
基本事实1
过不在同一条直线上的三点,有且只有一个平面。
基本事实2
如果一条直线上有两个点在一个平面内,那么这条直线在这个平面内。
基本事实3
如果两个不重合的平面有一个公共交点,那么它们有且只有一条经过该点的公共直线。
课堂小结
课程分析
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。
课程分析
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。
课程分析
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。
推论1
经过一条直线和该直线外一点, 有且只有一个 平面
推论2
经过两条相交直线, 有且只有一个 平面
推论3
经过两条平行直线, 有且只有一个 平面
课堂小结
课后作业
5
课后作业
1、判断题
(1)书面是平面 ( )
(2)平面α和平面β相交,它们只有有限个公共点 ( )
(3)两个平面有三个不共线的公共点,则这两个平面重合 ( )
2、多选题 ( )
A. 三个点确定一个平面
B. 一条直线和一个点确定一个平面
C. 两条不重合的直线确定一个平面
D. 圆上的任意三点,有且只有一个平面
E. 两个平面相交,只有一个公共点
课后作业
3、作图题
不共面的4个点,可以确定几个平面。
4、用符号表示下列语句,并画出相应的图形。
(1)A在直线m外,M在平面ABCD内。
(2)直线m在平面α内,又在平面β内。
(3)平面ABCD经过直线m,点P不在直线m上,点P在平面α内。
天道酬勤 勤能补拙
谢谢观看
第8章
8.4.1 平面
CONTENTS
目录
基本事实二
2
基本事实一
1
基本事实三
3
基本事实一
1
一、观察生活中的平面
桌面
海平面
黑板平面
桌面,海平面,都是水平放置平面
黑板平面,墙面,是竖直放置平面
二、平面的概念和画法
1、水平放置平面:
(1)通常用平行四边形表示平面
(2)水平边长画成邻边长的2倍
(3)锐角画成45°
平面的概念:
数学中的平面是指平坦、光滑、并且可以无限延展的图形。
平面的画法:
2、竖直放置平面:
(1)通常用平行四边形表示平面
(2)竖直边长画成邻边长的2倍
(3)锐角画成45°
平面
的表示
图形表示 (斜二侧画法)
符号表示
小写希腊字母表示
对角顶点表示法
顶点表示法
三、平面的表示
四、实验探索
小组合作:
分别用一个指尖、两个指尖、三个指尖表示点。用一个本子表示一个平面。看看几个指尖能平稳地将本子顶起来?
?
那么几个点能确定一个平面呢
我们知道:两点确定一条直线。
五、生活实例
?
那么几个点能确定一个平面呢
三脚架有与地面有三个接触点
(三个交点不在同一条直线上)
自行车有与地面有三个接触点
(三个交点不在同一条直线上)
通过实验观察,我们发现:
只有当三个指尖不在同一条直线上时,本子能被平稳地顶起来。
公理一:过不在一条直线上的三个点,有且只有一个平面。
简称:“不共线的三点,确定一个平面”。
α
A
C
B
图形语言:
符号语言:
A、B、C、三点不共线
有且只有一个 平面α
使得A∈α,B∈α,C∈α
六、基本事实1
一、多选题:
下列说法正确的是( )
A、 经过一点,有无数个平面
B、 经过两点,无法确定一个平面
C、 经过三点,有且只有三个平面
D、 不共线的三点确定一个平面
E、 过不在同一条直线上的三个点,
有且只有一个平面
七、例题讲解
例题解析:
A、正确。经过一个点,有无数个平面
B、正确。经过两个点,有无数个平面。所以,两点无法确定一个平面。
C、错误。
如果三点共线,那么经过这三个点,有无数个平面。
如果三点不共线,那么经过这三个点,有且只有一个平面。(公理一)
D、正确。公理一:“不共线的三点确定一个平面”。
E、正确。公理一:过不在同一条直线上的三个点,有且只有一个平面。
ABDE
√
√
√
√
×
因为:直线上有无数个点。所以把直线看成是无数个点的集合。
α
A
C
B
八、点,线,面的关系
A
l
点A 直线l
∈
因为:平面内有无数个点。所以把平面看成是无数个点的集合。
点A 平面α
点B 平面α
点C 平面α
直线AB 平面α
∈
∈
∈
一、单选题:
下列说法正确的是( )
A、经过一点,有且只有一个平面
B、经过两点,有且只有两个平面
C、经过三点,有且只有一个平面
D、经过不共线的三个点,
有且只有一个平面
二、填空题:
1、
经过共线的三点,有 平面。
不共线的三点可确定 平面。
2、如图:
A 平面α; BC 平面α。
α
A
C
B
D
无数个
1个
∈
九、课堂练习
基本事实二
2
师生合作:取出一根木棍。
(1)当木棍与桌面没有任何交点时。木棍与桌面有什么位置关系?
(2)将木棍上任意一点,固定在桌面上。木棍与桌面有什么位置关系?
(3)将木棍上任意两点,固定在桌面上。木棍与桌面有什么位置关系?
(2)
(3)
(1)
一、实验探索
线与面的位置关系 图象语言
文字语言
交点个数
直线a//平面α
直线a不在平面α内
直线a在平面α内
0个
1个
无数个
二、得出结论
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内。
当一条直线上的所有点都在平面内时,称直线在平面内,或平面经过直线。
图形语言:
符号语言:
α
A
B
A∈直线
B∈直线
A∈平面α
B∈平面α
直线 平面α
三、基本事实2
线与面的位置关系 图象语言
文字语言
符号语言
直线a//平面α
直线a不在平面α内
直线a在平面α内
a 平面α
四、得出结论
a 平面α
a 平面α
α
推论1
经过一条直线和该直线外一点, 平面
符号语言:
A 有且只有一个平面α,使得A∈平面α, 平面α
A
有且只有 1个
五、推论1
α
推论2
经过两条相交直线, 平面
符号语言:
1 ∩ 2=A 有且只有一个平面α,使得 1 平面α, 2 平面α
1
2
A
有且只有 1个
五、推论2
推论3
经过两条平行直线, 平面
α
1
2
符号语言:
1// 2 有且只有一个平面α,使得 1 平面α, 2 平面α
有且只有1个
五、推论3
一、判断题:
1、一条直线上有两个点在一个平面内,那么这条直线在平面内( )
2、一条直线上有两个点在一个平面内,那么这个平面经过这条直线。( )
3、平面内的任意两条直线,无法确定一个平面( )
4、经过一条直线和直线上一点,有且只有一个平面。( )
5、经过一条直线和直线外一点,有且只有一个平面。( )
答案解析:
1、正确。公理二:如果一条直线上有两个点在一个平面内,那么这条直线上的所有点都在这个平面内。
2、正确。当一条直线上的所有点都在平面内时,称直线在平面内,或平面经过直线。
3、错误。平面内的两条直线,要么平行,要么相交。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
4、错误
5、正确
推论1:经过一条直线和该直线外一点,有且只有一个平面。
√
√
×
√
×
六、课堂练习
基本事实三
3
思考:把三角板的一个角立在桌面上。三角板所在的平面与桌面是否只交于一点P?为什么?对此你有什么结论?
α
β
因为平面具有无限延展性。所以三角板所在的平面β与桌面α,相交于直线 。
由此,得到基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条经过该点的公共直线。
此时称两个平面相交。公共直线称为两个平面的交线。
P
符号语言:
P∈α,P∈β 有且只有一条直线 ,使得P∈ ,α∩β=
一、基本事实3
一、作图题:
试用符号语言表示下列语句,并画出相应的图形。
(1)点A、点B在直线 上,直线 在平面α内。
(2)平面α和平面β相交于直线 。
α
A
B
(1)
(2)
α
β
注意:
画两个平面相交时,一定要画出它们的交线。平面被遮挡部分用虚线表示或不画。
二、课堂练习
一、选择题
2、两个平面相交,那么它们有( )
A. 零个公共交点
B. 一个公共交点
C. 两个公共交点
D. 无数个公共交点
α
β
二、看图填空
A
A 平面α; A 平面β
B 平面α; B 平面β
平面α∩平面β= 。
二、课堂练习
B
D
∈
∈
∈
∈
AB
课堂小结
4
基本事实1
过不在同一条直线上的三点,有且只有一个平面。
基本事实2
如果一条直线上有两个点在一个平面内,那么这条直线在这个平面内。
基本事实3
如果两个不重合的平面有一个公共交点,那么它们有且只有一条经过该点的公共直线。
课堂小结
课程分析
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。
课程分析
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。
课程分析
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。
推论1
经过一条直线和该直线外一点, 有且只有一个 平面
推论2
经过两条相交直线, 有且只有一个 平面
推论3
经过两条平行直线, 有且只有一个 平面
课堂小结
课后作业
5
课后作业
1、判断题
(1)书面是平面 ( )
(2)平面α和平面β相交,它们只有有限个公共点 ( )
(3)两个平面有三个不共线的公共点,则这两个平面重合 ( )
2、多选题 ( )
A. 三个点确定一个平面
B. 一条直线和一个点确定一个平面
C. 两条不重合的直线确定一个平面
D. 圆上的任意三点,有且只有一个平面
E. 两个平面相交,只有一个公共点
课后作业
3、作图题
不共面的4个点,可以确定几个平面。
4、用符号表示下列语句,并画出相应的图形。
(1)A在直线m外,M在平面ABCD内。
(2)直线m在平面α内,又在平面β内。
(3)平面ABCD经过直线m,点P不在直线m上,点P在平面α内。
天道酬勤 勤能补拙
谢谢观看
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
