2007年整式(2)[上学期] 新人教版
文档属性
| 名称 | 2007年整式(2)[上学期] 新人教版 |

|
|
| 格式 | rar | ||
| 文件大小 | 623.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-29 00:00:00 | ||
图片预览



文档简介
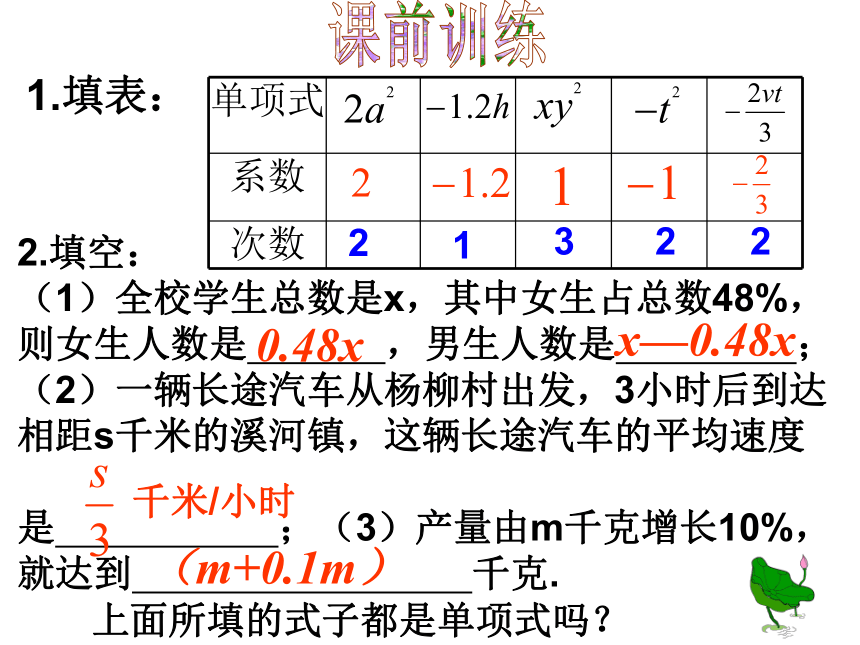
课件13张PPT。2.1 整式(2)1.数或字母的积,这样的式子叫做单项式.单独一个数或一个字母也叫做单项式.比如:200,a等都是单项式2.单项式中的数字因数叫做这个单项式的系数.一个单项式中,所有字母指数的和叫做这个单项式的次数.数200的系数是200,次数是0次;
字母a的系数是1,次数是1次.注意:(1)圆周率π是常数;(2)当一个单项式的系数是1或-1时,“1”通常省略不写。(3)单项式的系数应包括它前面的性质符号。知识回顾课前训练1.填表:213222.填空:
(1)全校学生总数是x,其中女生占总数48%,则女生人数是 ,男生人数是 ;
(2)一辆长途汽车从杨柳村出发,3小时后到达相距s千米的溪河镇,这辆长途汽车的平均速度
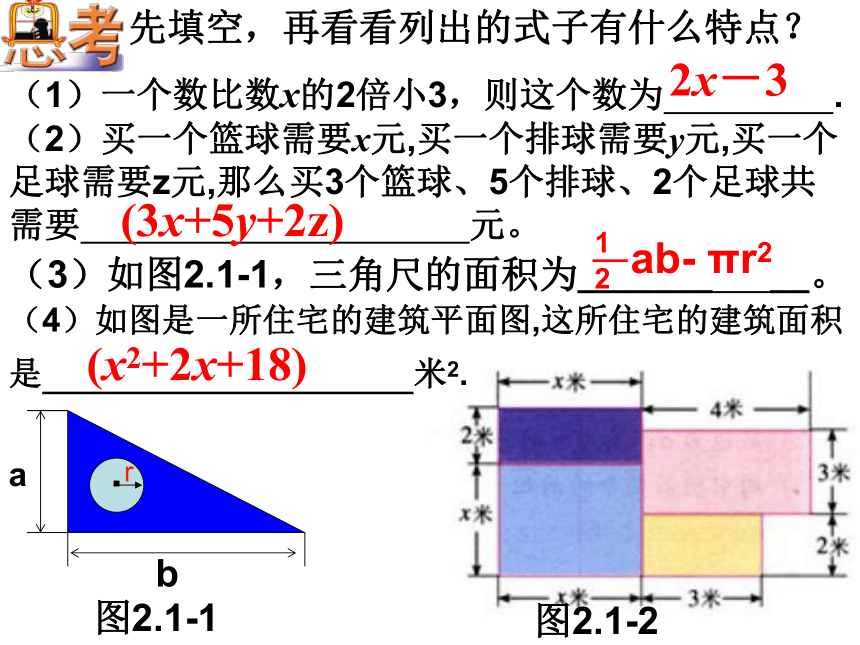
是 ;(3)产量由m千克增长10%,就达到 千克.0.48xx—0.48x千米/小时(m+0.1m)上面所填的式子都是单项式吗?(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,那么买3个篮球、5个排球、2个足球共需要 元。
(3x+5y+2z)(3)如图2.1-1,三角尺的面积为_______ __。图2.1-1(4)如图是一所住宅的建筑平面图,这所住宅的建筑面积是 米2.(x2+2x+18)先填空,再看看列出的式子有什么特点?(1)一个数比数x的2倍小3,则这个数为 .2x-3图2.1-23x+5y+2zx2+2x+182x-3观察发现这些式子的特点是:
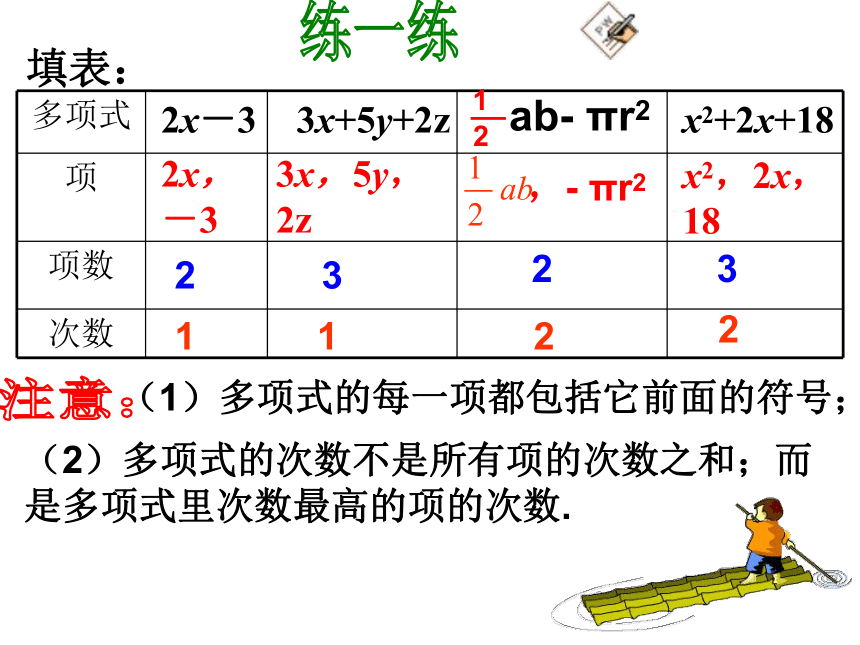
都是几个单项式的和.1、几个单项式的和叫做多项式。 2、在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。3、一般地,多项式里次数最高的项的次数,就是这个多项式的次数。——多项式多项式的定义及相关概念:练一练2x-33x+5y+2zx2+2x+182x,
-33x,5y,
2z,- πr2x2,2x,
1823231122填表:注意:(1)多项式的每一项都包括它前面的符号;(2)多项式的次数不是所有项的次数之和;而是多项式里次数最高的项的次数.例2:用多项式填空,并指出它们的项和次数:
(1)温度由t °C下降5 ° C后 是_______ ° C;
(2)甲数x的 与乙数y的 的差可以表示为
;
(3)如图2.1-3,圆环的面积为 ;
(4)如图2.1-4,钢管的体积是 .(t-5)解:(1)t-5,它的项是t和-5,次数是1;
(2) ,它的项是 和 ,次数是1;
(3) ,它的项是 和 ,次数是2;
(4) ,它的项是 和 ,次数是3;整式单项式多项式单项式与多项式统称整式。 代数式是用基本的运算符号(如加、减、乘、除等)把数、表示数的字母连接而成的式子.注意:代数式是不含等号和不等号的。代数式整式?单项式多项式(4)当出现除法时,一般用分数形式表示.书写代数式要注意的问题:(1)在代数式中要用到乘号,若数字与数字相乘,要用“×”号,若是数字与字母相乘或字母与字母相乘,通常简写作“·”或者省略不写.(2)数字因数、字母因数排列时,要把数字因数写在前边。(3)带分数与字母相乘时,应把带分数化为假分数。(5)几个字母因数排列时,要按字母表的顺序排列书写。(6)最后一步是加减运算的代数式,如若需要注明单位,那么必须用括号把整个式子括起来,后面再写单位。例3 一条河流的水流速度为2.5千米/时,如果已知船在静水中的速度,那么船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示?如果甲、乙两条船在静水中的速度分别是20千米/时和25千米/时,则它们在这条河流中顺水行驶和逆水行驶的速度各是多少?分析: 我们知道船在河流中行驶时,船的速度需要分两种情况讨论:顺水行驶:船的速度=船在静水中的速度+水流速度;逆水行驶:船的速度=船在静水中的速度-水流速度。 在上面的两个关系式中,如果用字母表示船在静水中的速度,那么船的速度就可以用含字母的式子表示出来。解:设船在静水中的速度为v千米/时,则当船顺水行驶时,船的速度为(v +2.5)千米/小时;当船逆水行驶时,船的速度为(v - 2.5)千米/小时。若甲船在静水中的速度是20千米/时,即v = 20,则v +2.5 =20 +2.5 =22.5,v - 2.5 =20 - 2.5 =17.5;若乙船在静水中的速度是35千米/时,即v = 30,则v +2.5 =35+2.5 =37.5,v - 2.5 =35- 2.5 =32.5; 由上可知,甲船顺水行驶的速度是22.5千米/时,逆水行驶的速度是17.5千米/时;乙船顺水行驶的速度是37.5千米/时,逆水行驶的速度是32.5千米/时。
字母a的系数是1,次数是1次.注意:(1)圆周率π是常数;(2)当一个单项式的系数是1或-1时,“1”通常省略不写。(3)单项式的系数应包括它前面的性质符号。知识回顾课前训练1.填表:213222.填空:
(1)全校学生总数是x,其中女生占总数48%,则女生人数是 ,男生人数是 ;
(2)一辆长途汽车从杨柳村出发,3小时后到达相距s千米的溪河镇,这辆长途汽车的平均速度
是 ;(3)产量由m千克增长10%,就达到 千克.0.48xx—0.48x千米/小时(m+0.1m)上面所填的式子都是单项式吗?(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,那么买3个篮球、5个排球、2个足球共需要 元。
(3x+5y+2z)(3)如图2.1-1,三角尺的面积为_______ __。图2.1-1(4)如图是一所住宅的建筑平面图,这所住宅的建筑面积是 米2.(x2+2x+18)先填空,再看看列出的式子有什么特点?(1)一个数比数x的2倍小3,则这个数为 .2x-3图2.1-23x+5y+2zx2+2x+182x-3观察发现这些式子的特点是:
都是几个单项式的和.1、几个单项式的和叫做多项式。 2、在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。3、一般地,多项式里次数最高的项的次数,就是这个多项式的次数。——多项式多项式的定义及相关概念:练一练2x-33x+5y+2zx2+2x+182x,
-33x,5y,
2z,- πr2x2,2x,
1823231122填表:注意:(1)多项式的每一项都包括它前面的符号;(2)多项式的次数不是所有项的次数之和;而是多项式里次数最高的项的次数.例2:用多项式填空,并指出它们的项和次数:
(1)温度由t °C下降5 ° C后 是_______ ° C;
(2)甲数x的 与乙数y的 的差可以表示为
;
(3)如图2.1-3,圆环的面积为 ;
(4)如图2.1-4,钢管的体积是 .(t-5)解:(1)t-5,它的项是t和-5,次数是1;
(2) ,它的项是 和 ,次数是1;
(3) ,它的项是 和 ,次数是2;
(4) ,它的项是 和 ,次数是3;整式单项式多项式单项式与多项式统称整式。 代数式是用基本的运算符号(如加、减、乘、除等)把数、表示数的字母连接而成的式子.注意:代数式是不含等号和不等号的。代数式整式?单项式多项式(4)当出现除法时,一般用分数形式表示.书写代数式要注意的问题:(1)在代数式中要用到乘号,若数字与数字相乘,要用“×”号,若是数字与字母相乘或字母与字母相乘,通常简写作“·”或者省略不写.(2)数字因数、字母因数排列时,要把数字因数写在前边。(3)带分数与字母相乘时,应把带分数化为假分数。(5)几个字母因数排列时,要按字母表的顺序排列书写。(6)最后一步是加减运算的代数式,如若需要注明单位,那么必须用括号把整个式子括起来,后面再写单位。例3 一条河流的水流速度为2.5千米/时,如果已知船在静水中的速度,那么船在这条河流中顺水行驶和逆水行驶的速度分别怎样表示?如果甲、乙两条船在静水中的速度分别是20千米/时和25千米/时,则它们在这条河流中顺水行驶和逆水行驶的速度各是多少?分析: 我们知道船在河流中行驶时,船的速度需要分两种情况讨论:顺水行驶:船的速度=船在静水中的速度+水流速度;逆水行驶:船的速度=船在静水中的速度-水流速度。 在上面的两个关系式中,如果用字母表示船在静水中的速度,那么船的速度就可以用含字母的式子表示出来。解:设船在静水中的速度为v千米/时,则当船顺水行驶时,船的速度为(v +2.5)千米/小时;当船逆水行驶时,船的速度为(v - 2.5)千米/小时。若甲船在静水中的速度是20千米/时,即v = 20,则v +2.5 =20 +2.5 =22.5,v - 2.5 =20 - 2.5 =17.5;若乙船在静水中的速度是35千米/时,即v = 30,则v +2.5 =35+2.5 =37.5,v - 2.5 =35- 2.5 =32.5; 由上可知,甲船顺水行驶的速度是22.5千米/时,逆水行驶的速度是17.5千米/时;乙船顺水行驶的速度是37.5千米/时,逆水行驶的速度是32.5千米/时。
