华师大版七年级下第10章图形的平移、旋转、中心对称导学案
文档属性
| 名称 | 华师大版七年级下第10章图形的平移、旋转、中心对称导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 71.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-08 00:00:00 | ||
图片预览




文档简介
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:图形的平移 课型:新授 教师寄语:好习惯是成功的开始
学习目标:1、根据日常生活认识图形的平移以及它的决定因素。
2、掌握图形平移的对应点、对应线段、对应角的识别。
3、找到图形平移的方向和距离
学习重点:理解平移是由移动方向和距离所决定。
学习难点:找到图形平移的方向和距离。
学习过程:
一、自主学习( 阅读课本P60—P61 )
1、什么叫图形的平移?
2、图形的平移由什么决定?
3、举出生活中平移的两个实例。
4、如图,△ABC是由△A’B’C’平移得到的,说出对应点,对应线段和对应角。并说出平移的方向和距离。
合作探究
1、判断下列现象是不是平移?
(1)门绕着门框旋转;
(2)汽车在笔直的公路上行驶;
(3)手扶电梯上的人由一层到了二层;
(4)手表时针的运动。
(5)奥运五环旗图案(在不考虑颜色前提下)形成过程.
2、如图,正方形ABCD沿AC的方向平移到正方形OEFG的位置,
请找出对应顶点、对应边和对应角。
交流展示
巩固训练
1.在下列六个图形中②、③、④、⑤、⑥中( )图案可以通过图案①平移得到的.
( http: / / www.21cnjy.com )
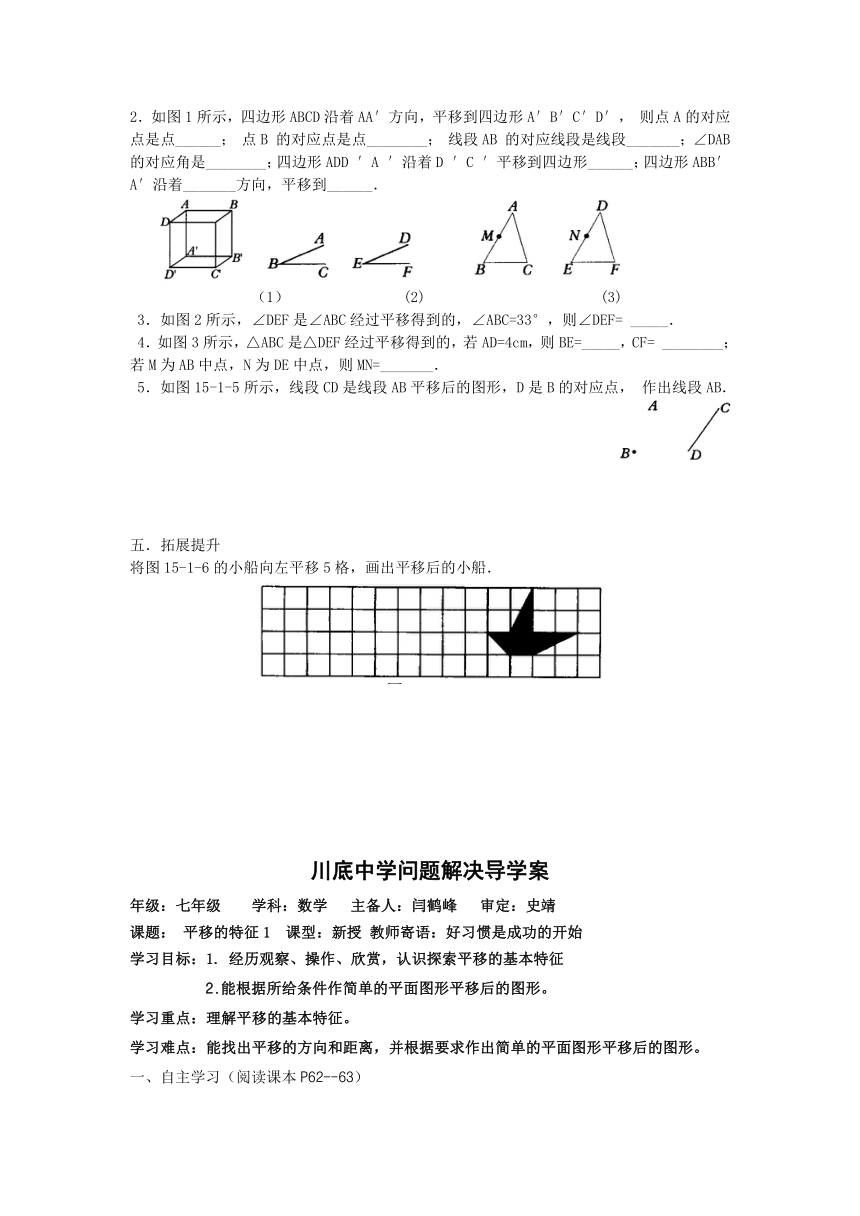
2.如图1所示,四边形ABCD沿着AA′ ( http: / / www.21cnjy.com )方向,平移到四边形A′B′C′D′,则点A的对应点是点______;点B的对应点是点________;线段AB的对应线段是线段_______;∠DAB的对应角是________;四边形ADD′A′沿着D′C′平移到四边形______;四边形ABB′A′沿着_______方向,平移到______.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3)
3.如图2所示,∠DEF是∠ABC经过平移得到的,∠ABC=33°,则∠DEF=_____.
4.如图3所示,△ABC是△DEF经过平 ( http: / / www.21cnjy.com )移得到的,若AD=4cm,则BE=_____,CF=________;若M为AB中点,N为DE中点,则MN=_______.
5.如图15-1-5所示,线段CD是线段AB平移后的图形,D是B的对应点,作出线段AB.
五.拓展提升
将图15-1-6的小船向左平移5格,画出平移后的小船.
( http: / / www.21cnjy.com )
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题: 平移的特征1 课型:新授 教师寄语:好习惯是成功的开始
学习目标:1. 经历观察、操作、欣赏,认识探索平移的基本特征
2.能根据所给条件作简单的平面图形平移后的图形。
学习重点:理解平移的基本特征。
学习难点:能找出平移的方向和距离,并根据要求作出简单的平面图形平移后的图形。
自主学习(阅读课本P62--63)
仔细观察图15.1.5,可得:
1、A B _____AB, A B _____AB, ∠B ______∠B
A C _____AC, A C _____AC, ∠C′_______∠C
BC与B C 呢?
从而可得平移的特征1: ___________________________________________________
_________________________________________________________________________________
2、观察图15.1.6, 将ΔABC沿着PQ的方向平移到ΔA B C 的位置,除了特征1之外,你还有什么发现?
AA ∥_____∥ _____
AA = _____= _____.
从而可得平移的特征2: ___________________________________________________
在课本上完成“试一试”。
思考:在平移过程中,对应点所连的线段可能在一条直线上吗?
二.合作探究
1、如图:ΔDEF可以看作ΔABC平移得到
1)平移的方向是 ;
平移的距离是 .
2)AB∥ ; AC∥ .
3)若BC=5cm,CF=3cm,
则BE= cm,CE= cm,EF= cm.
4)若连结A、D,与AD相等的线段是:
2、如图,将ΔABC沿EF方向平移3cm,
作出平移后的三角形。
三.交流展示
四、巩固训练
1、若∠A=60o,将∠A先向左平移1cm,再向下平移2cm,则∠A的大小( )
A、变小 B、变大
C、不变 D、无法确定
2、如图,在ΔABC中,∠A=40o,∠C=35o,
将ΔABC平移得到ΔDEF,DF与BC交于点G,
你能求出∠DGB与∠E的度数吗?
五、拓展提高
如图:在梯形ABCD中,A ( http: / / www.21cnjy.com )D∥BC,∠B+∠C=90o,点E在AD上,先将AB向右平移,使点A与点E重合,交BC于F,再将DC向左平移,使点D与点E重合,交BC于G,
(1)请判断ΔEFG的形状.
(2)若AD=3,FG=5,
求:BC的长
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:平移的特征2 课型:新授 教师寄语:好习惯是成功的开始
学习目标:1. 经历观察、操作、欣赏,认识探索平移的基本特征
2.能根据所给条件作简单的平面图形平移后的图形。
学习重点:理解平移的基本特征。
学习难点:能找出平移的方向和距离,并根据要求作出简单的平面图形平移后的图形。
一、自主学习(阅读课本P63-P64)
在课本的方格上完成“试一试”中要求的图形,并回答提出的问题。
在课本上画出“做一做”中要求的图形,并回答“做一做”提出的问题。你能用一句话来概括你的发现吗?
二、合作探究
1.如图所示,将字母A按箭头所指的方向,平移3cm,作出平移后的图形.
( http: / / www.21cnjy.com )
2、如图,直线a、b相交,试画出线段AB关于a的对称线段AB,再画出线段AB关于b的对称线段AB,并判断AB可否由AB平移得到。
三.交流展示
四.巩固训练
1、下列说法正确的是( )
A.图形平移的方向只有水平方向和竖直方向
B.图形平移后,它的位置、大小、形状都没改变
C.图形平移的方向不是唯一的,可向任何方向平移
D.图形平移后,对应线段不可能在同一直线上。
2、下列说法不正确的是( )
A.多次平移相当于一次平移 B.两次翻折相当于一次平移
C.当对称轴平行时,两次翻折相当于一次平移
D.平移时图形上每个点都移动了相同的距离
3、如图,ΔABC向右平移1cm之后得到ΔDEF,
如果AB=5cm,AC=3cm,EC=2cm,那么CF=___cm,
EF=_______cm,DE=______cm,DF=______cm.
五.拓展延伸
如图所示,在长方形地块内修筑同样宽的两条“之”字路,余下部分作为耕地,求道路宽为2m时,耕地面积为多少平方米?
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:图形的旋转 课型:新授 教师寄语:好习惯是成功的开始
学习目标:了解图形的旋转及图形旋转的基本特征,能够利用图形的旋转特 性进行计算。
学习重点:旋转的概念和性质。
学习难点:运用旋转的基础知识分析旋转图形的形成过程。
一、自主学习(阅读课本P65-P66,完成下列问题:)
1、旋转的定义:
__________________________________________________称为图形的旋转.
2、图形的旋转由__________、 ___________ 、 ____________决定。
3、完成课本上“试一试”和“做一做”
4、阅读课本例题,说明判断的依据。
二、合作探究
如图,ΔDAE绕点A按逆时针方向旋转到ΔBAC的位置,
请找出旋转中心、旋转角、对应顶点、对应边、对应角。
旋转中心是_______________________________
旋转角是_________________________________
对应点有_________________________________
对应边有_________________________________
对应角有_________________________________
交流展示
四、巩固训练
1、下列现象属于旋转的是( )
A.摩托车在急刹车时向前滑动
B.拧开自来水龙头的过程
C.空中飞舞的雪花
D。飞机起飞后冲向空中的过程
2、图形在旋转的过程中,其图形上的点所经过的路程是( )
A.直线 B.波浪线 C.折线 D.弧线
3、若线段AB绕点A顺时针旋转90后得到线段A B ,连接B B ,当线段AB=10cm时,线段B B =_________.
4、如图,等边三角形ABC经旋转后与等边三角形ACD重合,
如果把A点作为旋转中心,则至少把ΔABC顺时针旋转________度
后才能与ΔACD重合,A、B、C的对应点分别为________
如果把AC的中点作为旋转中心,则至少把ΔABC顺时针旋转_____度
后才能与ΔACD重合,A、B、C的对应点分别为_________
5、如图,在RtΔABC中,∠C=90°,∠CAB=30°,
把ΔABC绕着点A逆时针旋转60°,得到RtΔAED,
如果BC=啊,AC=吧,AB=c,
则EB的长为____________
五、拓展延伸
如图,P、Q、R分别是等边三角形ABC ( http: / / www.21cnjy.com )的三边AB、BC、CA的中点,M是BC上的任一点,把△PQM旋转到△PRN的位置,连接MN。(1)指出旋转中心与旋转的角度数;(2)说明△PMN是等边三角形的理由。
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题: 旋转的特征 课型:新授 教师寄语:好习惯是成功的开始
学习目标:理解旋转的基本特征,并能按要求作出简单平面图形旋转后的 图形
学习重点:理解旋转的基本特征。
学习难点:能找出旋转的中心方向和角度,并根据要求作出简单的平面图 形旋转后的图形。
一.自主学习:
(1)温故互查:
1、例举几个生活中的旋转现象
图形的旋转需满足哪些条件?
(2)设问导读:
1、认真观察课本图15.2.4与图15.2.5,你能发现哪些线段相等?哪些角相等?
2、图形旋转的特征有哪些?
合作探究
交流展示
四、巩固拓展:
1、下列现象属于旋转变换的是( )
A.物体在冰面上滑行 B.电梯向上运行
C.钟面上从12:00到12:15 分针的运动 D.镜子中人的像。
2、△ACE为等腰直角三角形,B为AE上一点,△ABC经过旋转到达△EDC的位置。
(1) 旋转中心为多少?
(2)旋转角是哪个角?
(3)若已知∠ACB=20°, 则∠CDE=_______,∠DEB=________
3、如图所示,以左图案的中心为旋转中心,将图案按 方向旋转
度,即可得到右边图案。
4、画出三角形ABC绕点O顺时针旋转90度后的图形。
( http: / / www.21cnjy.com )
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:旋转对称图形 课型:新授 教师寄语:好习惯是成功的开始
学习目标:认识旋转对称图形,并能按要求作出简单平面图形旋转后的图 形
重点:能按要求作出简单平面图形旋转后的图形
难点:理解旋转对称和旋转对称图形的不同
学习过程:
自主学习(阅读课本,回答问题)
1.旋转的特征是什么?
2、什么是旋转对称图形?例举几个生活中的旋转对称图形。
3、你能设计出一个旋转60度后能与自身重合的图形吗?
4、互相交流课本“做一做”中的问题
二.合作探究
三.交流展示
四.巩固拓展
1、将第一个图形按顺时针方向旋转90°后的图形是( )
2、如图,四边形ABCD是正方形,三角形ADE经顺时针旋转后与三角形ABF重合。
旋转中心是哪一点
旋转了多少度?
如果连接EF,那么三角形AEF是怎样的三角形?
( http: / / www.21cnjy.com )
3、下图是由三个正三角形组成的,它可以看作后一个是怎样由前一个得到的。
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:中心对称图形 课型:新授 教师寄语:好习惯是成功的开始
学习目标:1、认识中心对称,探索其基本性质,了解中心对称是旋转角为180度的旋转对称。
2、会画出已知图形关于某点的中心对称图形。
重点:理解中心对称及其性质
难点:会画出已知图形关于某点的中心对称图形
一:自主学习
(1)温故互查:
什么是旋转对称图形?试举例说明。
(2)、设问导读:
1、----------------------------------把这种图形叫中心对称图形。--------------叫对称中心。
2、关于某一点成中心对称的两个图形 ( http: / / www.21cnjy.com ),连接所有对称点的线段通过------------------,被-----------平分,对应线段与对应角都----------。
3、想一想:线段、三角形、平行四边形、圆是中心对称图形吗?如果是,对称中心又在哪里?
4、看课本第72页探索部分,回答后面的问题。
二.合作探究
三.交流展示
四.巩固拓展
1、单词NAME的四个字母中,是中心对称图形的是( )
2、下列说法中错误的是( )
A 关于某点对称的两个图形的对应点连成的线段,必被这点平分
B 关于某点成中心对称的两个图形能完全重合
C 若一个图形绕一点旋转一定角度,能与另一个图形完全重合,则这两个图形关于这点成中心对称。
3、已知三角形ABC和点O,画出三角形DEF,使它们关于点O成中心对称。
( http: / / www.21cnjy.com )
4、如图,已知AD是△ABC的中线,画出以点D为对称中心、与△ABC成中心对称的三角形
( http: / / www.21cnjy.com )
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:图形的全等 课型:新授 教师寄语:好习惯是成功的开始
学习目标:1、了解全等图形、全等多边形、全等三角形的概念和性质。
2、能辨别全等图形的对应元素。
重点:全等三角形的概念和性质 难点:辨别全等图形的对应元素
一.自主学习
(1)温故互查:
1、什么是中心对称图形?
2、图形经过图形的翻折、平移、旋转变换,它们的大小和形状有什么变化?
(2)设问导读:
1、什么是全等图形?
什么是全等三角形?
全等多边形的_____________________________分别相等。
例举几个生活中常见的全等图形。
看课本15.4.4图,指出它们的对应角、对应顶点、对应边。
二.合作交流
三.交流展示
巩固拓展
1、已知△ABC≌△CDA,指出它们的对应边、对应角。
( http: / / www.21cnjy.com )
2、如图,已知△ABC≌△ADC,∠BAC=60°, ∠ACD=23°,那么 ∠D等于多少度?
( http: / / www.21cnjy.com )
3、如图,已知△ABC≌△DEF,且AB=DE.试确定AC与DF的位置关系。并简单说明理由。
( http: / / www.21cnjy.com )
A
P
B
Q
M
C
R
N
(A)
(B)
(C)
(D)
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:图形的平移 课型:新授 教师寄语:好习惯是成功的开始
学习目标:1、根据日常生活认识图形的平移以及它的决定因素。
2、掌握图形平移的对应点、对应线段、对应角的识别。
3、找到图形平移的方向和距离
学习重点:理解平移是由移动方向和距离所决定。
学习难点:找到图形平移的方向和距离。
学习过程:
一、自主学习( 阅读课本P60—P61 )
1、什么叫图形的平移?
2、图形的平移由什么决定?
3、举出生活中平移的两个实例。
4、如图,△ABC是由△A’B’C’平移得到的,说出对应点,对应线段和对应角。并说出平移的方向和距离。
合作探究
1、判断下列现象是不是平移?
(1)门绕着门框旋转;
(2)汽车在笔直的公路上行驶;
(3)手扶电梯上的人由一层到了二层;
(4)手表时针的运动。
(5)奥运五环旗图案(在不考虑颜色前提下)形成过程.
2、如图,正方形ABCD沿AC的方向平移到正方形OEFG的位置,
请找出对应顶点、对应边和对应角。
交流展示
巩固训练
1.在下列六个图形中②、③、④、⑤、⑥中( )图案可以通过图案①平移得到的.
( http: / / www.21cnjy.com )
2.如图1所示,四边形ABCD沿着AA′ ( http: / / www.21cnjy.com )方向,平移到四边形A′B′C′D′,则点A的对应点是点______;点B的对应点是点________;线段AB的对应线段是线段_______;∠DAB的对应角是________;四边形ADD′A′沿着D′C′平移到四边形______;四边形ABB′A′沿着_______方向,平移到______.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3)
3.如图2所示,∠DEF是∠ABC经过平移得到的,∠ABC=33°,则∠DEF=_____.
4.如图3所示,△ABC是△DEF经过平 ( http: / / www.21cnjy.com )移得到的,若AD=4cm,则BE=_____,CF=________;若M为AB中点,N为DE中点,则MN=_______.
5.如图15-1-5所示,线段CD是线段AB平移后的图形,D是B的对应点,作出线段AB.
五.拓展提升
将图15-1-6的小船向左平移5格,画出平移后的小船.
( http: / / www.21cnjy.com )
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题: 平移的特征1 课型:新授 教师寄语:好习惯是成功的开始
学习目标:1. 经历观察、操作、欣赏,认识探索平移的基本特征
2.能根据所给条件作简单的平面图形平移后的图形。
学习重点:理解平移的基本特征。
学习难点:能找出平移的方向和距离,并根据要求作出简单的平面图形平移后的图形。
自主学习(阅读课本P62--63)
仔细观察图15.1.5,可得:
1、A B _____AB, A B _____AB, ∠B ______∠B
A C _____AC, A C _____AC, ∠C′_______∠C
BC与B C 呢?
从而可得平移的特征1: ___________________________________________________
_________________________________________________________________________________
2、观察图15.1.6, 将ΔABC沿着PQ的方向平移到ΔA B C 的位置,除了特征1之外,你还有什么发现?
AA ∥_____∥ _____
AA = _____= _____.
从而可得平移的特征2: ___________________________________________________
在课本上完成“试一试”。
思考:在平移过程中,对应点所连的线段可能在一条直线上吗?
二.合作探究
1、如图:ΔDEF可以看作ΔABC平移得到
1)平移的方向是 ;
平移的距离是 .
2)AB∥ ; AC∥ .
3)若BC=5cm,CF=3cm,
则BE= cm,CE= cm,EF= cm.
4)若连结A、D,与AD相等的线段是:
2、如图,将ΔABC沿EF方向平移3cm,
作出平移后的三角形。
三.交流展示
四、巩固训练
1、若∠A=60o,将∠A先向左平移1cm,再向下平移2cm,则∠A的大小( )
A、变小 B、变大
C、不变 D、无法确定
2、如图,在ΔABC中,∠A=40o,∠C=35o,
将ΔABC平移得到ΔDEF,DF与BC交于点G,
你能求出∠DGB与∠E的度数吗?
五、拓展提高
如图:在梯形ABCD中,A ( http: / / www.21cnjy.com )D∥BC,∠B+∠C=90o,点E在AD上,先将AB向右平移,使点A与点E重合,交BC于F,再将DC向左平移,使点D与点E重合,交BC于G,
(1)请判断ΔEFG的形状.
(2)若AD=3,FG=5,
求:BC的长
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:平移的特征2 课型:新授 教师寄语:好习惯是成功的开始
学习目标:1. 经历观察、操作、欣赏,认识探索平移的基本特征
2.能根据所给条件作简单的平面图形平移后的图形。
学习重点:理解平移的基本特征。
学习难点:能找出平移的方向和距离,并根据要求作出简单的平面图形平移后的图形。
一、自主学习(阅读课本P63-P64)
在课本的方格上完成“试一试”中要求的图形,并回答提出的问题。
在课本上画出“做一做”中要求的图形,并回答“做一做”提出的问题。你能用一句话来概括你的发现吗?
二、合作探究
1.如图所示,将字母A按箭头所指的方向,平移3cm,作出平移后的图形.
( http: / / www.21cnjy.com )
2、如图,直线a、b相交,试画出线段AB关于a的对称线段AB,再画出线段AB关于b的对称线段AB,并判断AB可否由AB平移得到。
三.交流展示
四.巩固训练
1、下列说法正确的是( )
A.图形平移的方向只有水平方向和竖直方向
B.图形平移后,它的位置、大小、形状都没改变
C.图形平移的方向不是唯一的,可向任何方向平移
D.图形平移后,对应线段不可能在同一直线上。
2、下列说法不正确的是( )
A.多次平移相当于一次平移 B.两次翻折相当于一次平移
C.当对称轴平行时,两次翻折相当于一次平移
D.平移时图形上每个点都移动了相同的距离
3、如图,ΔABC向右平移1cm之后得到ΔDEF,
如果AB=5cm,AC=3cm,EC=2cm,那么CF=___cm,
EF=_______cm,DE=______cm,DF=______cm.
五.拓展延伸
如图所示,在长方形地块内修筑同样宽的两条“之”字路,余下部分作为耕地,求道路宽为2m时,耕地面积为多少平方米?
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:图形的旋转 课型:新授 教师寄语:好习惯是成功的开始
学习目标:了解图形的旋转及图形旋转的基本特征,能够利用图形的旋转特 性进行计算。
学习重点:旋转的概念和性质。
学习难点:运用旋转的基础知识分析旋转图形的形成过程。
一、自主学习(阅读课本P65-P66,完成下列问题:)
1、旋转的定义:
__________________________________________________称为图形的旋转.
2、图形的旋转由__________、 ___________ 、 ____________决定。
3、完成课本上“试一试”和“做一做”
4、阅读课本例题,说明判断的依据。
二、合作探究
如图,ΔDAE绕点A按逆时针方向旋转到ΔBAC的位置,
请找出旋转中心、旋转角、对应顶点、对应边、对应角。
旋转中心是_______________________________
旋转角是_________________________________
对应点有_________________________________
对应边有_________________________________
对应角有_________________________________
交流展示
四、巩固训练
1、下列现象属于旋转的是( )
A.摩托车在急刹车时向前滑动
B.拧开自来水龙头的过程
C.空中飞舞的雪花
D。飞机起飞后冲向空中的过程
2、图形在旋转的过程中,其图形上的点所经过的路程是( )
A.直线 B.波浪线 C.折线 D.弧线
3、若线段AB绕点A顺时针旋转90后得到线段A B ,连接B B ,当线段AB=10cm时,线段B B =_________.
4、如图,等边三角形ABC经旋转后与等边三角形ACD重合,
如果把A点作为旋转中心,则至少把ΔABC顺时针旋转________度
后才能与ΔACD重合,A、B、C的对应点分别为________
如果把AC的中点作为旋转中心,则至少把ΔABC顺时针旋转_____度
后才能与ΔACD重合,A、B、C的对应点分别为_________
5、如图,在RtΔABC中,∠C=90°,∠CAB=30°,
把ΔABC绕着点A逆时针旋转60°,得到RtΔAED,
如果BC=啊,AC=吧,AB=c,
则EB的长为____________
五、拓展延伸
如图,P、Q、R分别是等边三角形ABC ( http: / / www.21cnjy.com )的三边AB、BC、CA的中点,M是BC上的任一点,把△PQM旋转到△PRN的位置,连接MN。(1)指出旋转中心与旋转的角度数;(2)说明△PMN是等边三角形的理由。
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题: 旋转的特征 课型:新授 教师寄语:好习惯是成功的开始
学习目标:理解旋转的基本特征,并能按要求作出简单平面图形旋转后的 图形
学习重点:理解旋转的基本特征。
学习难点:能找出旋转的中心方向和角度,并根据要求作出简单的平面图 形旋转后的图形。
一.自主学习:
(1)温故互查:
1、例举几个生活中的旋转现象
图形的旋转需满足哪些条件?
(2)设问导读:
1、认真观察课本图15.2.4与图15.2.5,你能发现哪些线段相等?哪些角相等?
2、图形旋转的特征有哪些?
合作探究
交流展示
四、巩固拓展:
1、下列现象属于旋转变换的是( )
A.物体在冰面上滑行 B.电梯向上运行
C.钟面上从12:00到12:15 分针的运动 D.镜子中人的像。
2、△ACE为等腰直角三角形,B为AE上一点,△ABC经过旋转到达△EDC的位置。
(1) 旋转中心为多少?
(2)旋转角是哪个角?
(3)若已知∠ACB=20°, 则∠CDE=_______,∠DEB=________
3、如图所示,以左图案的中心为旋转中心,将图案按 方向旋转
度,即可得到右边图案。
4、画出三角形ABC绕点O顺时针旋转90度后的图形。
( http: / / www.21cnjy.com )
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:旋转对称图形 课型:新授 教师寄语:好习惯是成功的开始
学习目标:认识旋转对称图形,并能按要求作出简单平面图形旋转后的图 形
重点:能按要求作出简单平面图形旋转后的图形
难点:理解旋转对称和旋转对称图形的不同
学习过程:
自主学习(阅读课本,回答问题)
1.旋转的特征是什么?
2、什么是旋转对称图形?例举几个生活中的旋转对称图形。
3、你能设计出一个旋转60度后能与自身重合的图形吗?
4、互相交流课本“做一做”中的问题
二.合作探究
三.交流展示
四.巩固拓展
1、将第一个图形按顺时针方向旋转90°后的图形是( )
2、如图,四边形ABCD是正方形,三角形ADE经顺时针旋转后与三角形ABF重合。
旋转中心是哪一点
旋转了多少度?
如果连接EF,那么三角形AEF是怎样的三角形?
( http: / / www.21cnjy.com )
3、下图是由三个正三角形组成的,它可以看作后一个是怎样由前一个得到的。
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:中心对称图形 课型:新授 教师寄语:好习惯是成功的开始
学习目标:1、认识中心对称,探索其基本性质,了解中心对称是旋转角为180度的旋转对称。
2、会画出已知图形关于某点的中心对称图形。
重点:理解中心对称及其性质
难点:会画出已知图形关于某点的中心对称图形
一:自主学习
(1)温故互查:
什么是旋转对称图形?试举例说明。
(2)、设问导读:
1、----------------------------------把这种图形叫中心对称图形。--------------叫对称中心。
2、关于某一点成中心对称的两个图形 ( http: / / www.21cnjy.com ),连接所有对称点的线段通过------------------,被-----------平分,对应线段与对应角都----------。
3、想一想:线段、三角形、平行四边形、圆是中心对称图形吗?如果是,对称中心又在哪里?
4、看课本第72页探索部分,回答后面的问题。
二.合作探究
三.交流展示
四.巩固拓展
1、单词NAME的四个字母中,是中心对称图形的是( )
2、下列说法中错误的是( )
A 关于某点对称的两个图形的对应点连成的线段,必被这点平分
B 关于某点成中心对称的两个图形能完全重合
C 若一个图形绕一点旋转一定角度,能与另一个图形完全重合,则这两个图形关于这点成中心对称。
3、已知三角形ABC和点O,画出三角形DEF,使它们关于点O成中心对称。
( http: / / www.21cnjy.com )
4、如图,已知AD是△ABC的中线,画出以点D为对称中心、与△ABC成中心对称的三角形
( http: / / www.21cnjy.com )
川底中学问题解决导学案
年级:七年级 学科:数学 主备人:闫鹤峰 审定:史靖
课题:图形的全等 课型:新授 教师寄语:好习惯是成功的开始
学习目标:1、了解全等图形、全等多边形、全等三角形的概念和性质。
2、能辨别全等图形的对应元素。
重点:全等三角形的概念和性质 难点:辨别全等图形的对应元素
一.自主学习
(1)温故互查:
1、什么是中心对称图形?
2、图形经过图形的翻折、平移、旋转变换,它们的大小和形状有什么变化?
(2)设问导读:
1、什么是全等图形?
什么是全等三角形?
全等多边形的_____________________________分别相等。
例举几个生活中常见的全等图形。
看课本15.4.4图,指出它们的对应角、对应顶点、对应边。
二.合作交流
三.交流展示
巩固拓展
1、已知△ABC≌△CDA,指出它们的对应边、对应角。
( http: / / www.21cnjy.com )
2、如图,已知△ABC≌△ADC,∠BAC=60°, ∠ACD=23°,那么 ∠D等于多少度?
( http: / / www.21cnjy.com )
3、如图,已知△ABC≌△DEF,且AB=DE.试确定AC与DF的位置关系。并简单说明理由。
( http: / / www.21cnjy.com )
A
P
B
Q
M
C
R
N
(A)
(B)
(C)
(D)
