【名师一号】2014-2015学年新课标A版高中数学必修1:第三章+++函数的应用+单元同步测试(含解析)
文档属性
| 名称 | 【名师一号】2014-2015学年新课标A版高中数学必修1:第三章+++函数的应用+单元同步测试(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 69.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-08 20:48:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第三章测试
(时间:120分钟 满分:150分)
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.二次函数f(x)=2x2+bx-3(b∈R)的零点个数是( )
A.0 B.1
C.2 D.不确定
解析 方程2x2+bx-3=0的判别式Δ=b2+24>0恒成立,所以方程有两个不等实根,因而函数f(x)有两个零点.【版权所有:21教育】
答案 C
2.若函数y=f(x)唯一的一个零点在区间(0,2),(1,2),(0,4)内,则下列命题中正确的是( )
A.函数f(x)在区间(0,1)内有零点
B.函数f(x)在区间(1,1.5)内有零点
C.函数f(x)在区间(2,4)内无零点
D.函数f(x)在区间(1,4)内无零点
解析 可用排除法,由题意知在(0,1)内没有零点,所以A错.B不一定,因为在(1,4)内一定有零点,所以D错,故C正确.
答案 C
3.根据表中的数据,可以判定方程ex-x-2=0的一个根所在的区间是( )
x -1 0 1 2 3
ex 0.37 1 2.72 7.39 20.09
x+2 1 2 3 4 5
A.(-1,0) B.(0,1)
C.(1,2) D.(2,3)
答案 C
4.方程lnx+2x-8=0根的个数是( )
A.0个 B.1个
C.2个 D.3个
解析 利用图象作答.
答案 B
5.下列函数中,随着x的增大,其增大速度最快的是( )
A.y=0.001ex B.y=1000lnx
C.y=x1000 D.y=1000·2x
解析 增大速度最快的应为指数型函数,又e≈2.718>2.
答案 A
6.已知直角梯形OABC中,AB∥OC, ( http: / / www.21cnjy.com )BC⊥OC,AB=1,OC=BC=2,直线x=t截这个梯形位于此直线左方的图形的面积(如图中阴影部分)为y,则函数y=f(t)的大致图象为图中的( )
解析 按一般方法求解,应先求出函数表达式, ( http: / / www.21cnjy.com )根据表达式确定图象,然而按小题小作的原则,不必求出解析式,观察图象不难发现C正确,因为一开始面积增长较快,当1≤t≤2时,面积平均增长,图象为直线,只有C适合这种规律.21世纪教育网版权所有
答案 C
7.已知函数f(x)=ex-x2+8x,则在下列区间中f(x)必有零点的是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
解析 f(x)=ex-x2+8x,f(-2 ( http: / / www.21cnjy.com ))=e-2-4-16<0,f(-1)=e-1-1-8<0,f(0)=e0=1>0,∴f(x)在区间(-1,0)内至少有一个零点,故选B.【来源:21·世纪·教育·网】
答案 B
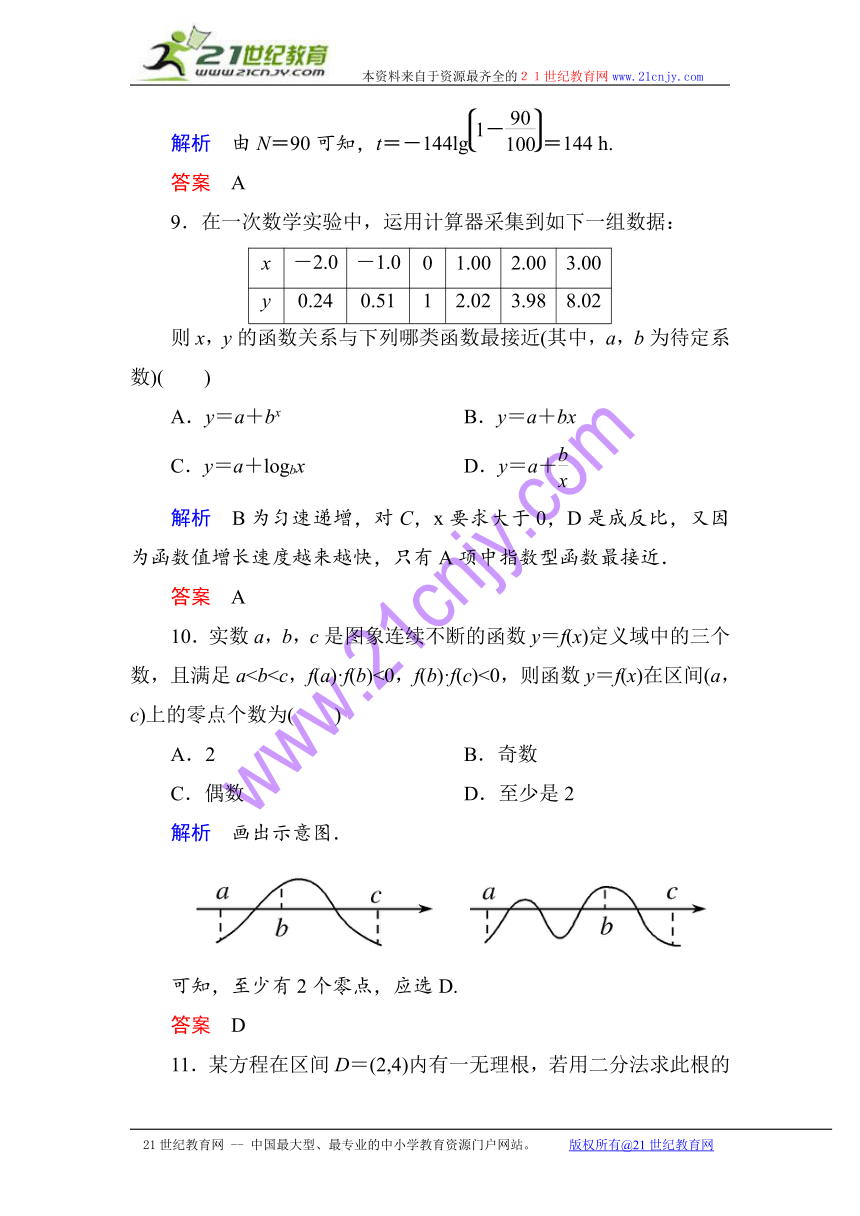
8.已知函数t=-144l ( http: / / www.21cnjy.com )g的图象可表示打字任务的“学习曲线”,其中t(h)表示达到打字水平N(字/min)所需的学习时间,N表示打字速度(字/min),则按此曲线要达到90字/min的水平,所需的学习时间是( )www.21-cn-jy.com
A.144 h B.90 h
C.60 h D.40 h
解析 由N=90可知,t=-144lg=144 h.
答案 A
9.在一次数学实验中,运用计算器采集到如下一组数据:
x -2.0 -1.0 0 1.00 2.00 3.00
y 0.24 0.51 1 2.02 3.98 8.02
则x,y的函数关系与下列哪类函数最接近(其中,a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=a+logbx D.y=a+
解析 B为匀速递增,对C,x要求大于0,D是成反比,又因为函数值增长速度越来越快,只有A项中指数型函数最接近.
答案 A
10.实数a,b,c是图象连续不断的函 ( http: / / www.21cnjy.com )数y=f(x)定义域中的三个数,且满足aA.2 B.奇数
C.偶数 D.至少是2
解析 画出示意图.
可知,至少有2个零点,应选D.
答案 D
11.某方程在区间D=(2,4)内有一无理根,若用二分法求此根的近似值,要使所得近似值的精确度达到0.1,则应将D分( )
A.2次 B.3次
C.4次 D.5次
解析 等分1次,区间长度为1,等分 ( http: / / www.21cnjy.com )2次区间长度为0.5,…,等分4次,区间长度为0.125,等分5次,区间长度为0.0625<0.1,符合题意.故选D.21cnjy.com
答案 D
12.西南大旱,为了保护水资源,提倡节约用水,某城市对居民生活用水,实行“阶梯水价”.计算方法如下表:21·世纪*教育网
每户每月用水量 水价
不超过12m3的部分 3元/m3
超过12 m3但不超过18 m3的部分 6元/m3
超过18 m3的部分 9元/m3
若某户居民本月交纳的水费为48元,则此户居民本月用水量( )
A.比12 m3少
B.比12 m3多,但不超过18 m3
C.比18 m3多
D.恰为12 m3
答案 B
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.为了保护学生的视力,课桌椅的 ( http: / / www.21cnjy.com )高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为y cm,椅子的高度为x cm,则y应是x的一次函数.下表列出两套符合条件的课桌椅的高度:
第一套 第二套
椅子高度x(cm) 40.0 37.0
课桌高度y(cm) 75.0 70.2
则y与x的函数关系为________.(不需注明定义域).
解析 依题意,由于课桌高度y是椅子高度x的一次函数,故可设y=ax+b(a≠0),将给出的符合条件的两套课桌椅的高度代入上述函数关系式,21·cn·jy·com
得
解得
所以y与x的函数关系式是y=1.6x+11.
答案 y=1.6x+11
14.用二分法求方程x3+4=6x2的一个近似解时,已经将一根锁定在区间(0,1)内,则下一步可断定该根所在的区间为________.
解析 设f(x)=x3-6x2+4,
显然f(0)>0,f(1)<0,
又f=3-6×2+4>0,
∴下一步可断定方程的根所在的区间为.
答案
15.函数f(x)=ax+b有一个零点是2,则函数g(x)=bx2-ax的零点是________.
解析 ∵f(x)=ax+b有一个零点是2,∴2a+b=0.而g(x)=bx2-ax=x(bx-a)=0,∴x=0,或x==-.2·1·c·n·j·y
答案 0,-
16.已知y=x(x-1)(x+1)的图象如 ( http: / / www.21cnjy.com )图所示.令f(x)=x(x-1)(x+1)+0.01,则下列关于f(x)=0的解叙述正确的是________.
①有三个实根;②x>1时恰有一实根;③当0解析 f(x)的图象是将函 ( http: / / www.21cnjy.com )数y=x(x-1)(x+1)的图象向上平移0.01个单位得到的,故f(x)的图象与x轴有三个交点,它们分别在区间(-∞,-1),和内,故只有①⑤正确.2-1-c-n-j-y
答案 ①⑤
三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分 ( http: / / www.21cnjy.com ))已知二次函数f(x)的图象过点(0,3),它的图象的对称轴为x=2,且f(x)的两个零点的平方和为10,求f(x)的解析式.www-2-1-cnjy-com
解 设f(x)=ax2+bx+c(a≠0),
由题意知,c=3,-=2.
设x1,x2是方程ax2+bx+c=0的两根,
则x1+x2=-,x1·x2=.
∵x+x=10,∴(x1+x2)2-2x1x2=10,即
2-=10,∴(-4)2-=10,
∴a=1,b=-4.
∴f(x)=x2-4x+3.
18.(本小题满分12分)A、B两城相 ( http: / / www.21cnjy.com )距100 km,在两地之间距A城x km处D地建一核电站给A、B两城供电,为保证城市安全.核电站与城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城为10亿度/月. 21*cnjy*com
(1)求x的范围;
(2)把月供电总费用y表示成x的函数;
(3)核电站建在距A城多远,才能使供电费用最小.
解 (1)x的取值范围为10≤x≤90;
(2)y=0.25×20x2+0.25×10(100-x2)
=5x2+(100-x)2(10≤x≤90);
(3)由y=5x2+(100-x)2=x2-500x+25000=2+.
则当x= km时,y最小.
故当核电站建在距A城 km时,才能使供电费用最小.
19.(本小题满分12分)某公司制定了 ( http: / / www.21cnjy.com )一个激励销售人员的奖励方案:当销售利润不超过15万元时,按销售利润的10%进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按2log5(A+1)进行奖励,没超出部分仍按销售利润的10%进行奖励.记资金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员的奖励方案的函数表达式;
(2)如果业务员老张获得5.5万元的资金,那么他的销售利润是多少万元?
解 (1)由题意,
得y=
(2)∵x∈(0,15]时,0.1x≤1.5,
又y=5.5>1.5,∴x>15,
所以1.5+2log5(x-14)=5.5,x=39.
答:老张的销售利润是39万元.
20.(本小题满分12分)某医药研 ( http: / / www.21cnjy.com )究所开发一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.【来源:21cnj*y.co*m】
(1)写出服药后y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫克血液中含药量不少于0.25微克时,治疗疾病有效.
①求服药一次治疗疾病有效的时间;
②当t=5时,第二次服药,求服药后30分钟,每毫升血液中的含药量.
解 (1)把点M(1,4)分别代入所给解析式可得
y=
(2)①∵解得0.0625≤t<1.
又解得1≤t≤5.
综上知,0.0625≤t≤5.
②由题设知,第二次服药后血液中每毫升的含药量
y=×4+23-5.5
=2+0.177=2.177(微克).
21.(本小题满分12分)已知函数f(x ( http: / / www.21cnjy.com ))=x-1+x2-2,试利用基本初等函数的图象判断f(x)有几个零点;并利用零点存在性定理确定各零点所在的范围(各区间长度不超过1).【出处:21教育名师】
解
由f(x)=0,得x-1=-x2+2,令y=x-1,y=-x2+2,其中抛物线顶点为(0,2),与x轴交于点(-2,0),(2,0).21教育名师原创作品
如图所示y=x-1,y=-x2+2的图象有3个交点,从而函数f(x)有3个零点.
∵x≠0,f(x)图象在(-∞,0),(0,+∞)上分别是连续不断的,
且f(-3)=>0,f(-2)=-<0,f=>0,
f(1)=-<0,f(2)=>0,
即f(-3)·f(-2)<0,f·f(1)<0,
f(2)·f(1)<0,
∴ 三个零点分别在区间(-3,-2),,(1,2)内.
22.(本小题满分12分)某县城出租 ( http: / / www.21cnjy.com )车的收费标准是:起步价是5元(乘车不超过3公里);行驶3公里后,每公里车费1.2元;行驶10公里后,每公里车费1.8元.21*cnjy*com
(1)写出车费与路程的关系式;
(2)一顾客行程30公里,为了省钱,他设计了两种乘车方案:
①分两段乘车:乘一车行15公里,换乘另一车再行15公里;
②分三段乘车:每乘10公里换一次车.
问哪一种方案最省钱.
解 (1)车费f(x)与路程x的关系式为
f(x)=
即f(x)=
(2)30公里不换车的车费为1.8×30-4.6=49.4(元);
方案①:行驶两个15公里的车费为
(1.8×15-4.6)×2=44.8(元);
方案②:行三个10公里的车费为
(1.2×10+1.4)×3=40.2(元).
由此可见,方案①和方案②都比不换车省钱,方案②比方案①更省钱.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第三章测试
(时间:120分钟 满分:150分)
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.二次函数f(x)=2x2+bx-3(b∈R)的零点个数是( )
A.0 B.1
C.2 D.不确定
解析 方程2x2+bx-3=0的判别式Δ=b2+24>0恒成立,所以方程有两个不等实根,因而函数f(x)有两个零点.【版权所有:21教育】
答案 C
2.若函数y=f(x)唯一的一个零点在区间(0,2),(1,2),(0,4)内,则下列命题中正确的是( )
A.函数f(x)在区间(0,1)内有零点
B.函数f(x)在区间(1,1.5)内有零点
C.函数f(x)在区间(2,4)内无零点
D.函数f(x)在区间(1,4)内无零点
解析 可用排除法,由题意知在(0,1)内没有零点,所以A错.B不一定,因为在(1,4)内一定有零点,所以D错,故C正确.
答案 C
3.根据表中的数据,可以判定方程ex-x-2=0的一个根所在的区间是( )
x -1 0 1 2 3
ex 0.37 1 2.72 7.39 20.09
x+2 1 2 3 4 5
A.(-1,0) B.(0,1)
C.(1,2) D.(2,3)
答案 C
4.方程lnx+2x-8=0根的个数是( )
A.0个 B.1个
C.2个 D.3个
解析 利用图象作答.
答案 B
5.下列函数中,随着x的增大,其增大速度最快的是( )
A.y=0.001ex B.y=1000lnx
C.y=x1000 D.y=1000·2x
解析 增大速度最快的应为指数型函数,又e≈2.718>2.
答案 A
6.已知直角梯形OABC中,AB∥OC, ( http: / / www.21cnjy.com )BC⊥OC,AB=1,OC=BC=2,直线x=t截这个梯形位于此直线左方的图形的面积(如图中阴影部分)为y,则函数y=f(t)的大致图象为图中的( )
解析 按一般方法求解,应先求出函数表达式, ( http: / / www.21cnjy.com )根据表达式确定图象,然而按小题小作的原则,不必求出解析式,观察图象不难发现C正确,因为一开始面积增长较快,当1≤t≤2时,面积平均增长,图象为直线,只有C适合这种规律.21世纪教育网版权所有
答案 C
7.已知函数f(x)=ex-x2+8x,则在下列区间中f(x)必有零点的是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
解析 f(x)=ex-x2+8x,f(-2 ( http: / / www.21cnjy.com ))=e-2-4-16<0,f(-1)=e-1-1-8<0,f(0)=e0=1>0,∴f(x)在区间(-1,0)内至少有一个零点,故选B.【来源:21·世纪·教育·网】
答案 B
8.已知函数t=-144l ( http: / / www.21cnjy.com )g的图象可表示打字任务的“学习曲线”,其中t(h)表示达到打字水平N(字/min)所需的学习时间,N表示打字速度(字/min),则按此曲线要达到90字/min的水平,所需的学习时间是( )www.21-cn-jy.com
A.144 h B.90 h
C.60 h D.40 h
解析 由N=90可知,t=-144lg=144 h.
答案 A
9.在一次数学实验中,运用计算器采集到如下一组数据:
x -2.0 -1.0 0 1.00 2.00 3.00
y 0.24 0.51 1 2.02 3.98 8.02
则x,y的函数关系与下列哪类函数最接近(其中,a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=a+logbx D.y=a+
解析 B为匀速递增,对C,x要求大于0,D是成反比,又因为函数值增长速度越来越快,只有A项中指数型函数最接近.
答案 A
10.实数a,b,c是图象连续不断的函 ( http: / / www.21cnjy.com )数y=f(x)定义域中的三个数,且满足a
C.偶数 D.至少是2
解析 画出示意图.
可知,至少有2个零点,应选D.
答案 D
11.某方程在区间D=(2,4)内有一无理根,若用二分法求此根的近似值,要使所得近似值的精确度达到0.1,则应将D分( )
A.2次 B.3次
C.4次 D.5次
解析 等分1次,区间长度为1,等分 ( http: / / www.21cnjy.com )2次区间长度为0.5,…,等分4次,区间长度为0.125,等分5次,区间长度为0.0625<0.1,符合题意.故选D.21cnjy.com
答案 D
12.西南大旱,为了保护水资源,提倡节约用水,某城市对居民生活用水,实行“阶梯水价”.计算方法如下表:21·世纪*教育网
每户每月用水量 水价
不超过12m3的部分 3元/m3
超过12 m3但不超过18 m3的部分 6元/m3
超过18 m3的部分 9元/m3
若某户居民本月交纳的水费为48元,则此户居民本月用水量( )
A.比12 m3少
B.比12 m3多,但不超过18 m3
C.比18 m3多
D.恰为12 m3
答案 B
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.为了保护学生的视力,课桌椅的 ( http: / / www.21cnjy.com )高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为y cm,椅子的高度为x cm,则y应是x的一次函数.下表列出两套符合条件的课桌椅的高度:
第一套 第二套
椅子高度x(cm) 40.0 37.0
课桌高度y(cm) 75.0 70.2
则y与x的函数关系为________.(不需注明定义域).
解析 依题意,由于课桌高度y是椅子高度x的一次函数,故可设y=ax+b(a≠0),将给出的符合条件的两套课桌椅的高度代入上述函数关系式,21·cn·jy·com
得
解得
所以y与x的函数关系式是y=1.6x+11.
答案 y=1.6x+11
14.用二分法求方程x3+4=6x2的一个近似解时,已经将一根锁定在区间(0,1)内,则下一步可断定该根所在的区间为________.
解析 设f(x)=x3-6x2+4,
显然f(0)>0,f(1)<0,
又f=3-6×2+4>0,
∴下一步可断定方程的根所在的区间为.
答案
15.函数f(x)=ax+b有一个零点是2,则函数g(x)=bx2-ax的零点是________.
解析 ∵f(x)=ax+b有一个零点是2,∴2a+b=0.而g(x)=bx2-ax=x(bx-a)=0,∴x=0,或x==-.2·1·c·n·j·y
答案 0,-
16.已知y=x(x-1)(x+1)的图象如 ( http: / / www.21cnjy.com )图所示.令f(x)=x(x-1)(x+1)+0.01,则下列关于f(x)=0的解叙述正确的是________.
①有三个实根;②x>1时恰有一实根;③当0
答案 ①⑤
三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分 ( http: / / www.21cnjy.com ))已知二次函数f(x)的图象过点(0,3),它的图象的对称轴为x=2,且f(x)的两个零点的平方和为10,求f(x)的解析式.www-2-1-cnjy-com
解 设f(x)=ax2+bx+c(a≠0),
由题意知,c=3,-=2.
设x1,x2是方程ax2+bx+c=0的两根,
则x1+x2=-,x1·x2=.
∵x+x=10,∴(x1+x2)2-2x1x2=10,即
2-=10,∴(-4)2-=10,
∴a=1,b=-4.
∴f(x)=x2-4x+3.
18.(本小题满分12分)A、B两城相 ( http: / / www.21cnjy.com )距100 km,在两地之间距A城x km处D地建一核电站给A、B两城供电,为保证城市安全.核电站与城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城为10亿度/月. 21*cnjy*com
(1)求x的范围;
(2)把月供电总费用y表示成x的函数;
(3)核电站建在距A城多远,才能使供电费用最小.
解 (1)x的取值范围为10≤x≤90;
(2)y=0.25×20x2+0.25×10(100-x2)
=5x2+(100-x)2(10≤x≤90);
(3)由y=5x2+(100-x)2=x2-500x+25000=2+.
则当x= km时,y最小.
故当核电站建在距A城 km时,才能使供电费用最小.
19.(本小题满分12分)某公司制定了 ( http: / / www.21cnjy.com )一个激励销售人员的奖励方案:当销售利润不超过15万元时,按销售利润的10%进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按2log5(A+1)进行奖励,没超出部分仍按销售利润的10%进行奖励.记资金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员的奖励方案的函数表达式;
(2)如果业务员老张获得5.5万元的资金,那么他的销售利润是多少万元?
解 (1)由题意,
得y=
(2)∵x∈(0,15]时,0.1x≤1.5,
又y=5.5>1.5,∴x>15,
所以1.5+2log5(x-14)=5.5,x=39.
答:老张的销售利润是39万元.
20.(本小题满分12分)某医药研 ( http: / / www.21cnjy.com )究所开发一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.【来源:21cnj*y.co*m】
(1)写出服药后y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫克血液中含药量不少于0.25微克时,治疗疾病有效.
①求服药一次治疗疾病有效的时间;
②当t=5时,第二次服药,求服药后30分钟,每毫升血液中的含药量.
解 (1)把点M(1,4)分别代入所给解析式可得
y=
(2)①∵解得0.0625≤t<1.
又解得1≤t≤5.
综上知,0.0625≤t≤5.
②由题设知,第二次服药后血液中每毫升的含药量
y=×4+23-5.5
=2+0.177=2.177(微克).
21.(本小题满分12分)已知函数f(x ( http: / / www.21cnjy.com ))=x-1+x2-2,试利用基本初等函数的图象判断f(x)有几个零点;并利用零点存在性定理确定各零点所在的范围(各区间长度不超过1).【出处:21教育名师】
解
由f(x)=0,得x-1=-x2+2,令y=x-1,y=-x2+2,其中抛物线顶点为(0,2),与x轴交于点(-2,0),(2,0).21教育名师原创作品
如图所示y=x-1,y=-x2+2的图象有3个交点,从而函数f(x)有3个零点.
∵x≠0,f(x)图象在(-∞,0),(0,+∞)上分别是连续不断的,
且f(-3)=>0,f(-2)=-<0,f=>0,
f(1)=-<0,f(2)=>0,
即f(-3)·f(-2)<0,f·f(1)<0,
f(2)·f(1)<0,
∴ 三个零点分别在区间(-3,-2),,(1,2)内.
22.(本小题满分12分)某县城出租 ( http: / / www.21cnjy.com )车的收费标准是:起步价是5元(乘车不超过3公里);行驶3公里后,每公里车费1.2元;行驶10公里后,每公里车费1.8元.21*cnjy*com
(1)写出车费与路程的关系式;
(2)一顾客行程30公里,为了省钱,他设计了两种乘车方案:
①分两段乘车:乘一车行15公里,换乘另一车再行15公里;
②分三段乘车:每乘10公里换一次车.
问哪一种方案最省钱.
解 (1)车费f(x)与路程x的关系式为
f(x)=
即f(x)=
(2)30公里不换车的车费为1.8×30-4.6=49.4(元);
方案①:行驶两个15公里的车费为
(1.8×15-4.6)×2=44.8(元);
方案②:行三个10公里的车费为
(1.2×10+1.4)×3=40.2(元).
由此可见,方案①和方案②都比不换车省钱,方案②比方案①更省钱.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
