【名师一号】2014-2015学年新课标A版高中数学必修3:第二章+统计++单元同步测试(含解析)
文档属性
| 名称 | 【名师一号】2014-2015学年新课标A版高中数学必修3:第二章+统计++单元同步测试(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 44.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-08 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第二章测试
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的)
1.某商场想通过检查发票及销售记录的2% ( http: / / www.21cnjy.com )来快速估计每月的销售总额.采取如下方法:从某本50张的发票存根中随机抽一张,如15号,然后按顺序往后将65号,115号,165号,…抽出,发票上的销售额组成一个调查样本.这种抽取样本的方法是( )
A.简单随机抽样 B.系统抽样
C.分层抽样 D.其他方式的抽样
答案 B
2.①某学校高二年级共有526人,为了调查 ( http: / / www.21cnjy.com )学生每天用于休息的时间,决定抽取10%的学生进行调查;②一次数学月考中,某班有10人在100分以上,32人在90~100分,12人低于90分,现从中抽取9人了解有关情况;③运动会工作人员为参加4×100 m接力赛的6支队伍安排跑道.就这三件事,恰当的抽样方法分别为( )
A.分层抽样、分层抽样、简单随机抽样
B.系统抽样、系统抽样、简单随机抽样
C.分层抽样、简单随机抽样、简单随机抽样
D.系统抽样、分层抽样、简单随机抽样
解析 ①中总体容量较多,抽取的样本容量较大 ( http: / / www.21cnjy.com ),用系统抽样比较恰当;②中考试成绩各分数段之间的同学有明显的差异,应按分层抽样比较恰当;③中个体较少,按简单随机抽样比较恰当.
答案 D
3.某中学有高一学生400 ( http: / / www.21cnjy.com )人,高二学生300人,高三学生500人,现用分层抽样的方法在这三个年级中抽取120人进行体能测试,则从高三抽取的人数应为( )21世纪教育网版权所有
A.40 B.48
C.50 D.80
解析 ∵一、二、三年级的人数比为4:3:5,∴从高三应抽取的人数为120×=50.
答案 C
4.将一个样本容量为100的数据分组,各组的频数如下:
(17,19],1;[19,21),1 ( http: / / www.21cnjy.com );(21,23],3;(23,25],3;(25,27],18;(27,29],16;(29,31],28;(31,33],30.2·1·c·n·j·y
根据样本频率分布,估计小于或等于29的数据大约占总体的( )
A.58% B.42%
C.40% D.16%
解析 依题意可得=42%.
答案 B
5.工人的月工资y(元)与劳动生产率x(千元)的回归方程为=50+80x,下列判断正确的是( )21·cn·jy·com
A.劳动生产率为1000元时,工资为130元
B.劳动生产率提高1000元,则工资提高80元
C.劳动生产率提高1000元,则工资提高130元
D.当月工资为210元时,劳动生产率为2000元
解析 由回归系数的意义知,当>0时,自变量和因变量正相关,当<0时,自变量和因变量负相关,回归直线的斜率=80,所以x每增加1个单位(千元),工人工资y平均增加80个单位(元),即劳动生产率提高1000元时,工资提高80元,故选B.
答案 B
6.甲、乙两名同学在五次数学测试中的成绩统计用茎叶图表示如下,若甲、乙两人的平均成绩分别用X甲,X乙表示,则下列结论正确的是( )【来源:21·世纪·教育·网】
A.X甲>X乙,甲比乙成绩稳定
B.X甲>X乙,乙比甲成绩稳定
C.X甲D.X甲解析 由茎叶图知,
X甲=×(68+69+70+71+72)=70,
X乙=×(63+68+69+69+71)=68,
∴X甲>X乙,且甲比乙成绩稳定.
答案 A
7.如果在一次实验中,测得(x,y ( http: / / www.21cnjy.com ))的四组数值分别是A(1,3),B(2,3.8),C(3,5.2),D(4,6),则y与x之间的回归直线方程是( )
A.=x+1.9 B.=1.04x+1.9
C.=0.95x+1.04 D.=1.05x-0.9
解析 =(1+2+3+4)=2.5,=(3+3.8+5.2+6)=4.5.
因为回归直线方程过样本点中心(,),代入验证知,应选B.
答案 B
8.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如下:
卡片号码 1 2 3 4 5 6 7 8 9 10
取到的次数 13 8 5 7 6 13 18 10 11 9
则取到号码为奇数的频率是( )
A.0.53 B.0.5
C.0.47 D.0.37
解析 取到号码为奇数的频数为13+5+6+18+11=53,故频率为0.53.
答案 A
9.甲、乙两支女子曲棍球队在去年的国际联赛中 ( http: / / www.21cnjy.com ),甲队平均每场进球数为3.2,全年比赛进球个数的标准差为3;乙队平均每场进球数是1.8,全年进球数的标准差为0.3.下列说法中,正确的个数为( )21·世纪*教育网
①甲队的技术比乙队好;②乙队发挥比甲队稳定;③乙队几乎每场都进球;④甲队的表现时好时坏.
A.1 B.2
C.3 D.4
解析 由平均数及方差的意义知,①,②,③,④都正确.
答案 D
10.10名工人某天生产同 ( http: / / www.21cnjy.com )一种零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )www-2-1-cnjy-com
A.a>b>c B.b>c>a
C.c>a>b D.c>b>a
解析 把10个数据从小到大排列为10,12,14,14,15,15,16,17,17,17.
∴中位数b=15,众数c=17,
平均数a=×(10+12+14×2+15×2+16+17×3)=14.7.
∴a答案 D
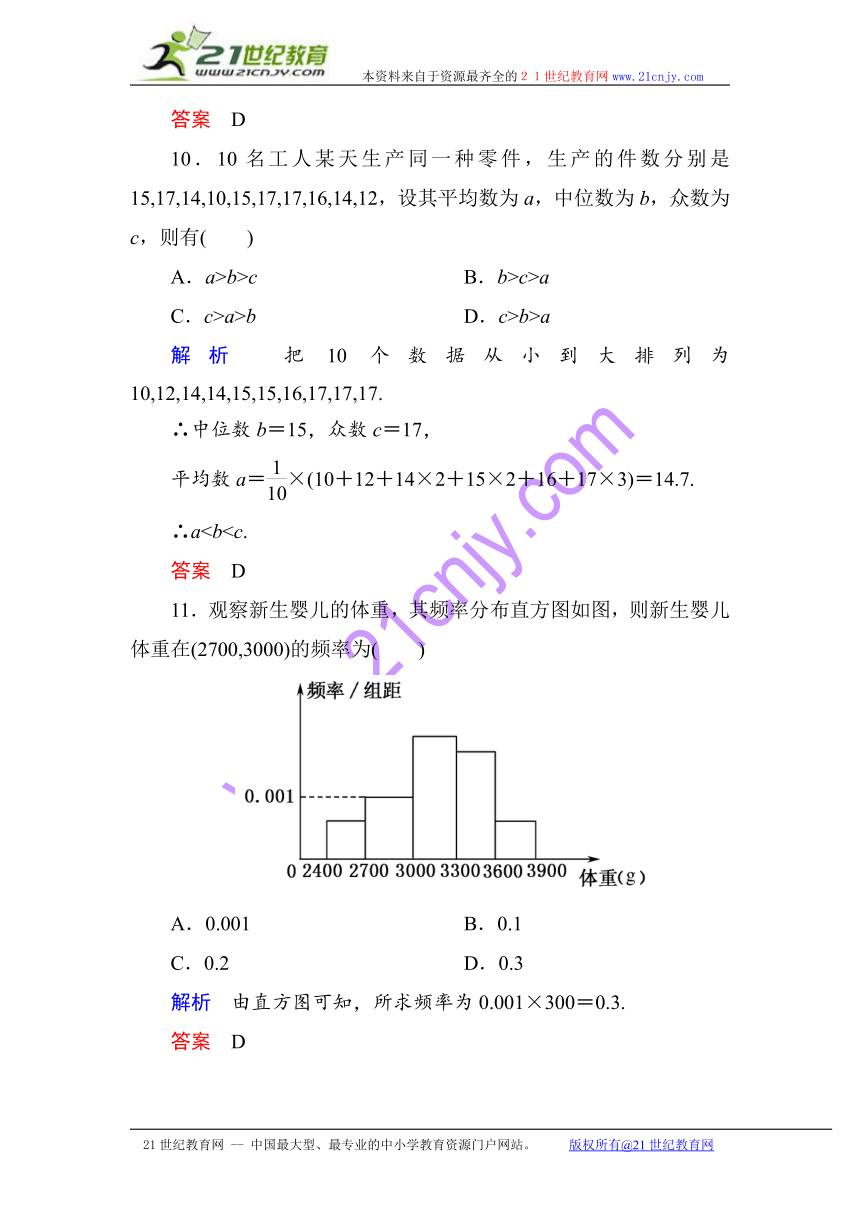
11.观察新生婴儿的体重,其频率分布直方图如图,则新生婴儿体重在(2700,3000)的频率为( )2-1-c-n-j-y
A.0.001 B.0.1
C.0.2 D.0.3
解析 由直方图可知,所求频率为0.001×300=0.3.
答案 D
12.设矩形的长为a,宽 ( http: / / www.21cnjy.com )为b,其比满足b?a=≈0.618,这种矩形给人以美感,称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:21教育网
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数与标准值0.618比较,正确结论是( )
A.甲批次的总体平均数与标准值更接近
B.乙批次的总体平均数与标准值更接近
C.两个批次总体平均数与标准值接近程度相同
D.两个批次总体平均数与标准值接近程度不能确定
解析 甲批次的样本平均数为
×(0.598+0.625+0.628+0.595+0.639)
=0.617;
乙批次的样本平均数为
×(0.618+0.613+0.592+0.622+0.620)
=0.613.
所以可估计:甲批次的总体平均数与标准值更接近.
答案 A
二、填空题(本大题共4小题,每小题5分,满分20分.把答案填在题中横线上)
13.将某班的60名学生编号为:01, ( http: / / www.21cnjy.com )02,…,60,采用系统抽样方法抽取一个容量为5的样本,且随机抽得的一个号码为04,则剩下的四个号码依次是________. 21*cnjy*com
解析 由于从60个中抽取5个,故分组的间距为12,又第一组的号码为04,所以其他四个号码依次是16,28,40,52.
答案 16,28,40,52
14.如图是CBA篮球联赛中,甲、乙两名运动员某赛季一些场次得分的茎叶图,则平均得分高的运动员是________.
解析 由茎叶图知平均得分高的运动员是甲,或计算得甲=20.4,2=19.3,甲>乙.
答案 甲
15.防疫站对学生进行身体健康调查,采 ( http: / / www.21cnjy.com )用分层抽样法抽取.某中学共有学生1600名,抽取一个容量为200的样本,已知女生比男生少抽了10人,则该校的女生人数应为________人.
解析 由题意知,样本中有女生95人,男生105人,则全校共有女生为95÷=760人.
答案 760
16.某市高三数学抽样考试中,对9 ( http: / / www.21cnjy.com )0分以上(含90分)的成绩进行统计,其频率分布图如图所示,若130~140分数段的人数为90人,则90~100分数段的人数为________.【来源:21cnj*y.co*m】
解析 由频率分布图知,设90~100分数段的人数为x,则=,∴x=720.
答案 720
三、解答题(本大题共6小题,满分70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)已知一组数据从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,求这组数据的平均数与方差.
解 由于数据-1,0,4,x,7,14的中位数为5,
所以=5,x=6.
设这组数据的平均数为,方差为s2,由题意得
=×(-1+0+4+6+7+14)=5,
s2=×[(-1-5)2+(0-5)2+(4-5)2+(6-5)2+(7-5)2+(14-5)2]=.【出处:21教育名师】
18.(12分)为了了解小学生的体能情况 ( http: / / www.21cnjy.com ),抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组频率分别为0.1,0.3,0.4,第一小组的频数为5.【版权所有:21教育】
(1)求第四小组的频率;
(2)参加这次测试的学生有多少人;
(3)若次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率是多少.
解 (1)由累积频率为1知,第四小组的频率为
1-0.1-0.3-0.4=0.2.
(2)设参加这次测试的学生有x人,则0.1x=5,
∴x=50.即参加这次测试的学生有50人.
(3)达标率为0.3+0.4+0.2=90%,
所以估计该年级学生跳绳测试的达标率为90%.
19.(12分)对某400件元件进行寿命追踪调查情况频率分布如下:
寿命(h) 频率
[500,600) 0.10
[600,700) 0.15
[700,800) 0.40
[800,900) 0.20
[900,1000] 0.15
合计 1
(1)列出寿命与频数对应表;
(2)估计元件寿命在[500,800)内的频率;
(3)估计元件寿命在700 h以上的频率.
解 (1)寿命与频数对应表:
寿命(h) [500,600) [600,700) [700,800) [800,900) [900,1000]
频数 40 60 160 80 60
(2)估计该元件寿命在[500,800)内的频率为
0.10+0.15+0.40=0.65.
(3)估计该元件寿命在700 h以上的频率为
0.40+0.20+0.15=0.75.
20.(12分)两台机床同时生产一种零件,在10天中,两台机床每天的次品数如下:
甲 1,0,2,0,2,3,0,4,1,2
乙 1,3,2,1,0,2,1,1,0,1
(1)哪台机床次品数的平均数较小?
(2)哪台机床的生产状况比较稳定?
解 (1)甲=(1+0+2+0+2+3+0+4+1+2)×=1.5,
乙=(1+3+2+1+0+2+1+1+0+1)×=1.2.
∵甲>乙,
∴乙车床次品数的平均数较小.
(2)s=[(1-1.5)2+( ( http: / / www.21cnjy.com )0-1.5)2+(2-1.5)2+(0-1.5)2+(2-1.5)2+(3-1.5)2+(0-1.5)2+(4-1.5)2+(1-1.5)2+(2-1.5)2]=1.65,
同理s=0.76,
∵s>s,
∴乙车床的生产状况比较稳定.
21.(12分)某学校暑假中组织了一次 ( http: / / www.21cnjy.com )旅游活动,分两组,一组去武夷山,另一组去海南,且每个职工至多参加其中一组.在参加旅游活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.去武夷山组的职工占参加活动总人数的,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:www.21-cn-jy.com
(1)去海南组中,青年人、中年人、老年人分别所占的比例;
(2)去海南组中,青年人、中年人、老年人分别应抽取的人数.
解 (1)设去武夷山组的人数为x,去海南组中,青年人、中年人、老年人各占比例分别为a,b,c,则有
=47.5%,=10%,
解得b=50%,c=10%.所以a=100%-b-c=40%.
故去海南组中,青年人、中年人、老年人各占比例分别为40%、50%、10%.
(2)去海南组中,抽取的青年人 ( http: / / www.21cnjy.com )数为200××40%=60(人);抽取的中年人数为200××50%=75(人);抽取的老年人数为200××10%=15(人).21cnjy.com
22.(12分)某个体服装店经营各种服装,在某周内获纯利润y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表:
x 3 4 5 6 7 8 9
y 66 69 73 81 89 90 91
已知:=280,iyi=3487.
(1)求,;
(2)画出散点图;
(3)观察散点图,若y与x线性相关,请求纯利润y与每天销售件数x之间的回归直线方程.
解 (1)==6,
==≈79.86.
(2)散点图如图所示.
(3)观察散点图知,y与x线性相关.设回归直线方程为=x+.
∵=280,iyi=3487,
=6,=,
∴===4.75.
=-6×4.75≈51.36.
∴回归直线方程为=4.75x+51.36.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第二章测试
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的)
1.某商场想通过检查发票及销售记录的2% ( http: / / www.21cnjy.com )来快速估计每月的销售总额.采取如下方法:从某本50张的发票存根中随机抽一张,如15号,然后按顺序往后将65号,115号,165号,…抽出,发票上的销售额组成一个调查样本.这种抽取样本的方法是( )
A.简单随机抽样 B.系统抽样
C.分层抽样 D.其他方式的抽样
答案 B
2.①某学校高二年级共有526人,为了调查 ( http: / / www.21cnjy.com )学生每天用于休息的时间,决定抽取10%的学生进行调查;②一次数学月考中,某班有10人在100分以上,32人在90~100分,12人低于90分,现从中抽取9人了解有关情况;③运动会工作人员为参加4×100 m接力赛的6支队伍安排跑道.就这三件事,恰当的抽样方法分别为( )
A.分层抽样、分层抽样、简单随机抽样
B.系统抽样、系统抽样、简单随机抽样
C.分层抽样、简单随机抽样、简单随机抽样
D.系统抽样、分层抽样、简单随机抽样
解析 ①中总体容量较多,抽取的样本容量较大 ( http: / / www.21cnjy.com ),用系统抽样比较恰当;②中考试成绩各分数段之间的同学有明显的差异,应按分层抽样比较恰当;③中个体较少,按简单随机抽样比较恰当.
答案 D
3.某中学有高一学生400 ( http: / / www.21cnjy.com )人,高二学生300人,高三学生500人,现用分层抽样的方法在这三个年级中抽取120人进行体能测试,则从高三抽取的人数应为( )21世纪教育网版权所有
A.40 B.48
C.50 D.80
解析 ∵一、二、三年级的人数比为4:3:5,∴从高三应抽取的人数为120×=50.
答案 C
4.将一个样本容量为100的数据分组,各组的频数如下:
(17,19],1;[19,21),1 ( http: / / www.21cnjy.com );(21,23],3;(23,25],3;(25,27],18;(27,29],16;(29,31],28;(31,33],30.2·1·c·n·j·y
根据样本频率分布,估计小于或等于29的数据大约占总体的( )
A.58% B.42%
C.40% D.16%
解析 依题意可得=42%.
答案 B
5.工人的月工资y(元)与劳动生产率x(千元)的回归方程为=50+80x,下列判断正确的是( )21·cn·jy·com
A.劳动生产率为1000元时,工资为130元
B.劳动生产率提高1000元,则工资提高80元
C.劳动生产率提高1000元,则工资提高130元
D.当月工资为210元时,劳动生产率为2000元
解析 由回归系数的意义知,当>0时,自变量和因变量正相关,当<0时,自变量和因变量负相关,回归直线的斜率=80,所以x每增加1个单位(千元),工人工资y平均增加80个单位(元),即劳动生产率提高1000元时,工资提高80元,故选B.
答案 B
6.甲、乙两名同学在五次数学测试中的成绩统计用茎叶图表示如下,若甲、乙两人的平均成绩分别用X甲,X乙表示,则下列结论正确的是( )【来源:21·世纪·教育·网】
A.X甲>X乙,甲比乙成绩稳定
B.X甲>X乙,乙比甲成绩稳定
C.X甲
X甲=×(68+69+70+71+72)=70,
X乙=×(63+68+69+69+71)=68,
∴X甲>X乙,且甲比乙成绩稳定.
答案 A
7.如果在一次实验中,测得(x,y ( http: / / www.21cnjy.com ))的四组数值分别是A(1,3),B(2,3.8),C(3,5.2),D(4,6),则y与x之间的回归直线方程是( )
A.=x+1.9 B.=1.04x+1.9
C.=0.95x+1.04 D.=1.05x-0.9
解析 =(1+2+3+4)=2.5,=(3+3.8+5.2+6)=4.5.
因为回归直线方程过样本点中心(,),代入验证知,应选B.
答案 B
8.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如下:
卡片号码 1 2 3 4 5 6 7 8 9 10
取到的次数 13 8 5 7 6 13 18 10 11 9
则取到号码为奇数的频率是( )
A.0.53 B.0.5
C.0.47 D.0.37
解析 取到号码为奇数的频数为13+5+6+18+11=53,故频率为0.53.
答案 A
9.甲、乙两支女子曲棍球队在去年的国际联赛中 ( http: / / www.21cnjy.com ),甲队平均每场进球数为3.2,全年比赛进球个数的标准差为3;乙队平均每场进球数是1.8,全年进球数的标准差为0.3.下列说法中,正确的个数为( )21·世纪*教育网
①甲队的技术比乙队好;②乙队发挥比甲队稳定;③乙队几乎每场都进球;④甲队的表现时好时坏.
A.1 B.2
C.3 D.4
解析 由平均数及方差的意义知,①,②,③,④都正确.
答案 D
10.10名工人某天生产同 ( http: / / www.21cnjy.com )一种零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )www-2-1-cnjy-com
A.a>b>c B.b>c>a
C.c>a>b D.c>b>a
解析 把10个数据从小到大排列为10,12,14,14,15,15,16,17,17,17.
∴中位数b=15,众数c=17,
平均数a=×(10+12+14×2+15×2+16+17×3)=14.7.
∴a
11.观察新生婴儿的体重,其频率分布直方图如图,则新生婴儿体重在(2700,3000)的频率为( )2-1-c-n-j-y
A.0.001 B.0.1
C.0.2 D.0.3
解析 由直方图可知,所求频率为0.001×300=0.3.
答案 D
12.设矩形的长为a,宽 ( http: / / www.21cnjy.com )为b,其比满足b?a=≈0.618,这种矩形给人以美感,称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:21教育网
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数与标准值0.618比较,正确结论是( )
A.甲批次的总体平均数与标准值更接近
B.乙批次的总体平均数与标准值更接近
C.两个批次总体平均数与标准值接近程度相同
D.两个批次总体平均数与标准值接近程度不能确定
解析 甲批次的样本平均数为
×(0.598+0.625+0.628+0.595+0.639)
=0.617;
乙批次的样本平均数为
×(0.618+0.613+0.592+0.622+0.620)
=0.613.
所以可估计:甲批次的总体平均数与标准值更接近.
答案 A
二、填空题(本大题共4小题,每小题5分,满分20分.把答案填在题中横线上)
13.将某班的60名学生编号为:01, ( http: / / www.21cnjy.com )02,…,60,采用系统抽样方法抽取一个容量为5的样本,且随机抽得的一个号码为04,则剩下的四个号码依次是________. 21*cnjy*com
解析 由于从60个中抽取5个,故分组的间距为12,又第一组的号码为04,所以其他四个号码依次是16,28,40,52.
答案 16,28,40,52
14.如图是CBA篮球联赛中,甲、乙两名运动员某赛季一些场次得分的茎叶图,则平均得分高的运动员是________.
解析 由茎叶图知平均得分高的运动员是甲,或计算得甲=20.4,2=19.3,甲>乙.
答案 甲
15.防疫站对学生进行身体健康调查,采 ( http: / / www.21cnjy.com )用分层抽样法抽取.某中学共有学生1600名,抽取一个容量为200的样本,已知女生比男生少抽了10人,则该校的女生人数应为________人.
解析 由题意知,样本中有女生95人,男生105人,则全校共有女生为95÷=760人.
答案 760
16.某市高三数学抽样考试中,对9 ( http: / / www.21cnjy.com )0分以上(含90分)的成绩进行统计,其频率分布图如图所示,若130~140分数段的人数为90人,则90~100分数段的人数为________.【来源:21cnj*y.co*m】
解析 由频率分布图知,设90~100分数段的人数为x,则=,∴x=720.
答案 720
三、解答题(本大题共6小题,满分70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)已知一组数据从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,求这组数据的平均数与方差.
解 由于数据-1,0,4,x,7,14的中位数为5,
所以=5,x=6.
设这组数据的平均数为,方差为s2,由题意得
=×(-1+0+4+6+7+14)=5,
s2=×[(-1-5)2+(0-5)2+(4-5)2+(6-5)2+(7-5)2+(14-5)2]=.【出处:21教育名师】
18.(12分)为了了解小学生的体能情况 ( http: / / www.21cnjy.com ),抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组频率分别为0.1,0.3,0.4,第一小组的频数为5.【版权所有:21教育】
(1)求第四小组的频率;
(2)参加这次测试的学生有多少人;
(3)若次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率是多少.
解 (1)由累积频率为1知,第四小组的频率为
1-0.1-0.3-0.4=0.2.
(2)设参加这次测试的学生有x人,则0.1x=5,
∴x=50.即参加这次测试的学生有50人.
(3)达标率为0.3+0.4+0.2=90%,
所以估计该年级学生跳绳测试的达标率为90%.
19.(12分)对某400件元件进行寿命追踪调查情况频率分布如下:
寿命(h) 频率
[500,600) 0.10
[600,700) 0.15
[700,800) 0.40
[800,900) 0.20
[900,1000] 0.15
合计 1
(1)列出寿命与频数对应表;
(2)估计元件寿命在[500,800)内的频率;
(3)估计元件寿命在700 h以上的频率.
解 (1)寿命与频数对应表:
寿命(h) [500,600) [600,700) [700,800) [800,900) [900,1000]
频数 40 60 160 80 60
(2)估计该元件寿命在[500,800)内的频率为
0.10+0.15+0.40=0.65.
(3)估计该元件寿命在700 h以上的频率为
0.40+0.20+0.15=0.75.
20.(12分)两台机床同时生产一种零件,在10天中,两台机床每天的次品数如下:
甲 1,0,2,0,2,3,0,4,1,2
乙 1,3,2,1,0,2,1,1,0,1
(1)哪台机床次品数的平均数较小?
(2)哪台机床的生产状况比较稳定?
解 (1)甲=(1+0+2+0+2+3+0+4+1+2)×=1.5,
乙=(1+3+2+1+0+2+1+1+0+1)×=1.2.
∵甲>乙,
∴乙车床次品数的平均数较小.
(2)s=[(1-1.5)2+( ( http: / / www.21cnjy.com )0-1.5)2+(2-1.5)2+(0-1.5)2+(2-1.5)2+(3-1.5)2+(0-1.5)2+(4-1.5)2+(1-1.5)2+(2-1.5)2]=1.65,
同理s=0.76,
∵s>s,
∴乙车床的生产状况比较稳定.
21.(12分)某学校暑假中组织了一次 ( http: / / www.21cnjy.com )旅游活动,分两组,一组去武夷山,另一组去海南,且每个职工至多参加其中一组.在参加旅游活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.去武夷山组的职工占参加活动总人数的,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:www.21-cn-jy.com
(1)去海南组中,青年人、中年人、老年人分别所占的比例;
(2)去海南组中,青年人、中年人、老年人分别应抽取的人数.
解 (1)设去武夷山组的人数为x,去海南组中,青年人、中年人、老年人各占比例分别为a,b,c,则有
=47.5%,=10%,
解得b=50%,c=10%.所以a=100%-b-c=40%.
故去海南组中,青年人、中年人、老年人各占比例分别为40%、50%、10%.
(2)去海南组中,抽取的青年人 ( http: / / www.21cnjy.com )数为200××40%=60(人);抽取的中年人数为200××50%=75(人);抽取的老年人数为200××10%=15(人).21cnjy.com
22.(12分)某个体服装店经营各种服装,在某周内获纯利润y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表:
x 3 4 5 6 7 8 9
y 66 69 73 81 89 90 91
已知:=280,iyi=3487.
(1)求,;
(2)画出散点图;
(3)观察散点图,若y与x线性相关,请求纯利润y与每天销售件数x之间的回归直线方程.
解 (1)==6,
==≈79.86.
(2)散点图如图所示.
(3)观察散点图知,y与x线性相关.设回归直线方程为=x+.
∵=280,iyi=3487,
=6,=,
∴===4.75.
=-6×4.75≈51.36.
∴回归直线方程为=4.75x+51.36.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
