【名师一号】2014-2015学年新课标A版高中数学必修3:第三章++概率+单元同步测试(含解析)
文档属性
| 名称 | 【名师一号】2014-2015学年新课标A版高中数学必修3:第三章++概率+单元同步测试(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 68.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-08 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第三章测试
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的)
1.先后抛掷2枚一分、二分的硬币,观察落地后硬币的正、反面情况,则下列事件包含3个基本事件的是( )21世纪教育网版权所有
A.至少一枚硬币正面向上
B.只有一枚硬币正面向上
C.两枚硬币都是正面向上
D.两枚硬币一枚正面向上,另一枚正面向下
解析 先后抛掷2枚一分、二分的硬币,其结 ( http: / / www.21cnjy.com )果有4种情形:“1正2正”、“1正2反”、“1反2正”、“1反2反”,可得“至少一枚硬币正面向上”包含3个基本事件. 21*cnjy*com
答案 A
2.下列命题:
①对立事件一定是互斥事件;②若A,B为两个 ( http: / / www.21cnjy.com )随机事件,则P(A∪B)=P(A)+P(B);③若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A,B满足P(A)+P(B)=1,则A与B是对立事件.
其中正确命题的个数是( )
A.1 B.2
C.3 D.4
解析 ①正确;②不正确,当A与B是互斥事件 ( http: / / www.21cnjy.com )时,才有P(A∪B)=P(A)+P(B),对于任意两个事件A,B满足P(A∪B)=P(A)+P(B)-P(AB);③也不正确.P(A)+P(B)+P(C)不一定等于1,还可能小于1;④也不正确.例如:袋中有大小相同的红、黄、黑、绿4个球,从袋中任摸一个球,设事件A={摸到红球或黄球},事件B={摸到黄球或黑球},显然事件A与B不互斥,但P(A)+P(B)=+=1.
答案 A
3.掷一枚均匀的硬币,如果连续抛掷1000次,那么第999次出现正面向上的概率是( )
A. B.
C. D.
解析 投掷一枚均匀的硬币正面向上的概率为,它不因抛掷的次数而变化,因此抛掷一次正面向上的概率为,抛掷第999次正面向上的概率还是.【出处:21教育名师】
答案 D
4.某导演先从2个金鸡奖和 ( http: / / www.21cnjy.com )3个百花奖的5位演员名单中挑选2名演主角,后又从剩下的演员中挑选1名演配角.这位导演挑选出2个金鸡奖演员和1个百花奖演员的概率为( )
A. B.
C. D.
解析 设2个金鸡奖演员编号为1,2,3 ( http: / / www.21cnjy.com )个百花奖演员编号为3,4,5.从编号为1,2,3,4,5的演员中任选3名有10种挑选方法:(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),其中挑选出2名金鸡奖和1名百花奖的有3种:(1,2,3),(1,2,4),(1,2,5),故所求的概率为P=.
答案 D
5.设某厂产品的次品率为3%,估计该厂8000件产品中次品的件数为( )
A.3 B.160
C.240 D.7480
解析 次品数为8000×3%=240.
答案 C
6.有四个游戏盘,将它们水平放稳后,在上面扔一颗小玻璃球,若小球落在阴影部分,则可中奖,小明要想增加中奖机会,应选择的游戏盘是( )
解析 由几何概型概率公式知,图中中 ( http: / / www.21cnjy.com )奖的概率依次是P(A)=,P(B)=,P(C)==,P(D)=,因此,要想增加中奖机会,应选择A盘.
答案 A
7.在线段AB上任取三个点x1,x2,x3,则x2位于x1与x3之间的概率为( )
A. B.
C. D.1
解析 由于x1,x2,x3是任意的 ( http: / / www.21cnjy.com ),它们的排列次序有:x1x2x3,x2x1x3,x2x3x1,x3x2x1,x1x3x2,x3x1x2,共6种情况.其中x2在x1与x3之间有两种情况,故所求概率为=.
答案 B
8.小明同学的QQ密码是由0,1,2,3,4 ( http: / / www.21cnjy.com ),5,6,7,8,9这10个数字中的6个数字组成的六位数,由于长时间未登录QQ,小明忘记了密码的最后一个数字,如果小明登录QQ时密码的最后一个数字随意选取,则恰好能登录的概率是( )21·cn·jy·com
A. B.
C. D.
解析 只考虑最后一位数字即可,从0至9这10个数字中任取一个,作为密码的最后一位数字有10种可能,其中只有一种可能登录成功,故其概率为.
答案 D
9.某人从甲地去乙地共走了 ( http: / / www.21cnjy.com )500 m,途中要过一条宽为x m的河流,他不小心把一件物品丢在途中,若物品掉在河里就找不到,若物品不掉在河里,则能找到,已知该物品能找到的概率为,则河宽为( )
A.100 m B.80 m
C. 50 m D.40 m
解析 设河宽x m,则1-=,∴x=100 (m).
答案 A
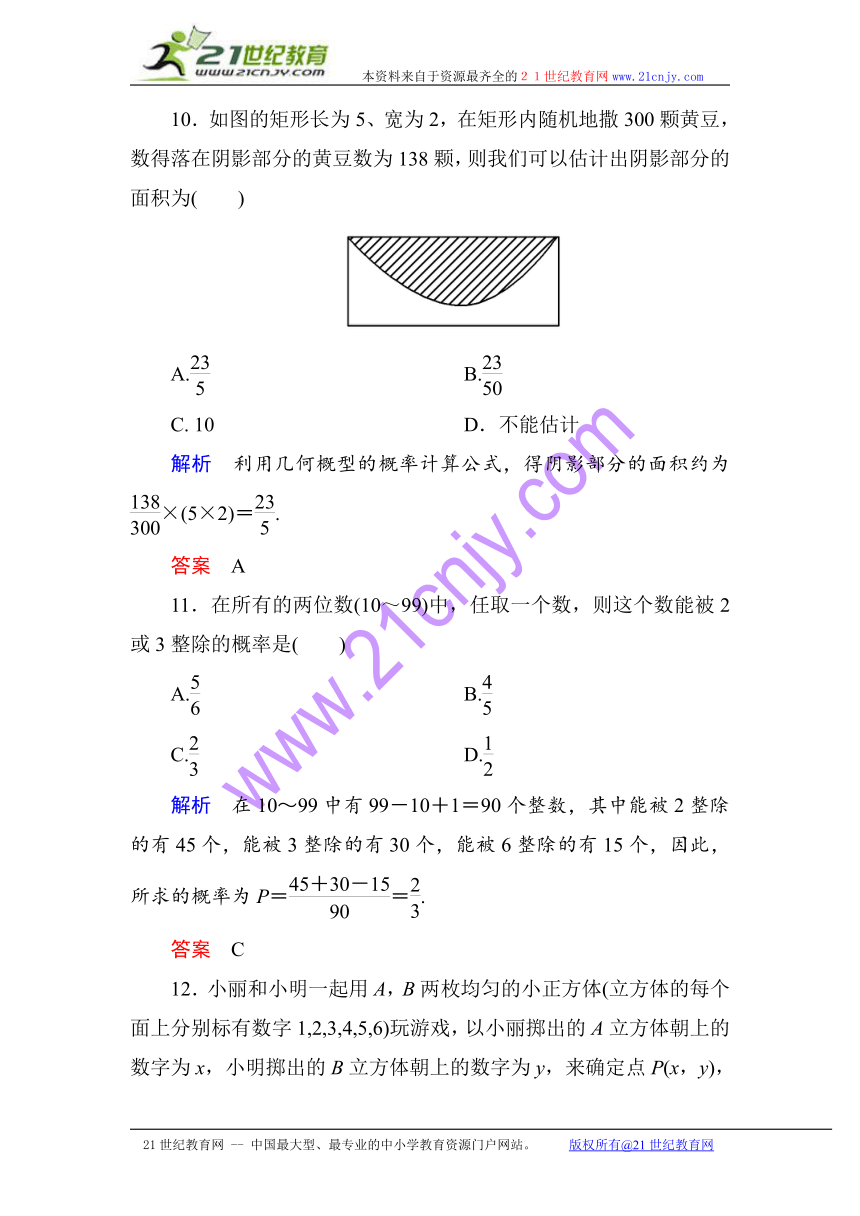
10.如图的矩形长为5、宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分的面积为( )
A. B.
C. 10 D.不能估计
解析 利用几何概型的概率计算公式,得阴影部分的面积约为×(5×2)=.
答案 A
11.在所有的两位数(10~99)中,任取一个数,则这个数能被2或3整除的概率是( )
A. B.
C. D.
解析 在10~99中有9 ( http: / / www.21cnjy.com )9-10+1=90个整数,其中能被2整除的有45个,能被3整除的有30个,能被6整除的有15个,因此,所求的概率为P==.21cnjy.com
答案 C
12.小丽和小明一起用A,B两枚均匀的 ( http: / / www.21cnjy.com )小正方体(立方体的每个面上分别标有数字1,2,3,4,5,6)玩游戏,以小丽掷出的A立方体朝上的数字为x,小明掷出的B立方体朝上的数字为y,来确定点P(x,y),那么他们各掷一次所确定的点P(x,y)落在抛物线y=-x2+4x上的概率为( )
A. B.
C. D.
解析 根据题意,两人各掷小正方体一次, ( http: / / www.21cnjy.com )每人都有6种可能性,则点P(x,y)的情况有6×6=36种可能,而y=-x2+4x=-(x-2)2+4,即(x-2)2+y=4,易得在抛物线上的点有(2,4),(1,3),(3,3)共3种.因此满足条件的概率为=.
答案 C
二、填空题(本大题共4小题,每小题5分,满分20分.把答案填在题中横线上)
13.一种投掷骰子的游戏规则是:交 ( http: / / www.21cnjy.com )2元钱可掷一次骰子,若骰子朝上的点数是1,则中奖2元;若点数是2或3,则中奖1元,若点数是4,5或6,则无奖,某人投掷一次,那么中奖的概率是______.
解析 由题意知,投掷一次骰子若点数为1,2,3则获奖,若出现点数4,5,6无奖,所以中奖的概率为.
答案
14.设集合A={0,1,2},B={0 ( http: / / www.21cnjy.com ),1,2},分别从集合A和B中随机取一个数a和b,确定平面上一个点P(a,b),设“点P(a,b)落在直线x+y=n上”为事件Cn(0≤n≤4,n∈N),若事件Cn的概率最大,则n的可能值为________.【版权所有:21教育】
解析 基本事件为点(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),总数为9.www.21-cn-jy.com
当n=0时,落在直线x+y=0上的点有1个(0,0);
当n=1时,落在直线x+y=1上的点有2个,(0,1)和(1,0);
当n=2时,落在直线x+y=2上的点有(1,1),(2,0),(0,2),共3个;
当n=3时,落在直线x+y=3上的点有(1,2),(2,1)共2个;
当n=4时,落在直线x+y=4上的点只有(2,2)1个.
因此,当Cn的概率最大时,n=2.
答案 2
15.已知区域E={(x,y)|0≤ ( http: / / www.21cnjy.com )x≤3,0≤y≤2},F={(x,y)|0≤x≤3,0≤y≤2,x≥y},若向区域E内随机投掷一点,则该点落入区域F内的概率为________.21·世纪*教育网
解析 依题意可知,本问题属于几何概型,区域E和区域F的对应图形如图所示.
其中区域E的面积为3×2=6,区域F的面积为×(1+3)×2=4,所以向区域E内随机投掷一点,该点落入区域F内的概率为P==.
答案
16.从4名男生和2名女生中任选3人参加演讲比赛,所选3人中至少有1名女生的概率为,那么所选3人中都是男生的概率为________.www-2-1-cnjy-com
解析 设A={3人中至少有1名女生},B={3人中都是男生},则A,B为对立事件,∴P(B)=1-P(A)=.2-1-c-n-j-y
答案
三、解答题(本大题共6小题,满分70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)某学校篮球队,羽毛球队、乒乓球队各有10名队员,某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求:21教育名师原创作品
(1)该队员只属于一支球队的概率;
(2)该队员最多属于两支球队的概率.
解 由图知,三支球队共有队员10+4+3+3=20人,其中只参加一支球队的队员有5+4+3=12人,参加两支球队的队员有1+2+3=6人.
(1)设“该队员只属于一支球队”为事件A,
则P(A)==.
(2)设“该队员最多属于两支球队”为事件B,
则P(B)=+==.(或P(B)=1-=)
18.(12分)高一军训时,某同学射击一次,命中10环,9环,8环的概率分别为0.13,0.28,0.31.
(1)求射击一次,命中10环或9环的概率;
(2)求射击一次,至少命中8环的概率;
(3)求射击一次,命中环数小于9环的概率.
解 设事件“射击一次,命中i环”为事件 ( http: / / www.21cnjy.com )Ai(0≤i≤10,且i∈N),且Ai两两互斥.由题意知P(A10)=0.13,P(A9)=0.28,P(A8)=0.31.
(1)记“射击一次,命中10环或9环”的事件为A,那么P(A)=P(A10)+P(A9)=0.13+0.28=0.41.
(2)记“射击一次,至少命中8环”的事件为B,那么P(B)=P(A10)+P(A9)+P(A8)=0.13+0.28+0.31=0.72.
(3)记“射击一次,命中环数小于9环”的事件为C,则C与A是对立事件,∴P(C)=1-P(A)=1-0.41=0.59.
19.(12分)水池的容积是2 ( http: / / www.21cnjy.com )0 m3,向水池注水的水龙头A和水龙头B的流速都是1 m3/h,它们在一昼夜内随机开放(0~24小时),求水池不溢出水的概率.(精确到0.01)
解 设水龙头A开x小时,水龙头B开y小时,若水池不溢出水,则x+y≤20,
记“水池不溢出水”为事件M,则M所占区 ( http: / / www.21cnjy.com )域面积为×20×20=200,整个区域的面积为24×24=576,由几何概型的概率公式,得P(M)=≈0.35,
即水池不溢出水的概率为0.35.
20.(12分)A、B两个箱子分别装有标号为0,1,2的三种卡片,每种卡片的张数如表所示.
( http: / / www.21cnjy.com )
(1)从A、B箱中各取1张卡片,用x表示取出的2张卡片的数字之积,求x=2的概率;
(2)从A、B箱中各取1张卡片,用y表示取出的2张卡片的数字之和,求x=0,y=2的概率.
解 依题意知,从A、B箱中各取1张卡片,其基本事件有6×5=30个.
(1)记事件C为“从A、B箱中各取1张卡片,2张卡片的数字之积等于2”,则C包含5个基本事件,由古典概型的概率公式得P(C)==.
(2)记事件D为“从A、B箱中各取1张卡片,其数字之和为2且积为0”,则包含10个基本事件,则P(D)==.
21.(12分)某中学生物兴趣小组在学校生 ( http: / / www.21cnjy.com )物园地种植了一批名贵树苗,为了解树苗生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米).把这些高度列成了如下的频数分布表:
组别 [40,50) [50,60) [60,70) [70,80) [80,90) [90,100]
频数 2 3 14 15 12 4
(1)在这批树苗中任取一棵,其高度在85厘米以上的概率大约是多少?
(2)这批树苗的平均高度大约是多少?(计算时可以用组中值代替各组数据的平均值)
(3)为了进一步获得研究资料 ( http: / / www.21cnjy.com ),若从[40,50)组中移出一棵树苗,从[90,100]组中移出两棵树苗进行试验研究,则[40,50)组中的树苗A和[90,100]组中的树苗C同时被移出的概率是多少?21教育网
解 (1)由已知,高度在85厘米以上的树苗大约有6+4=10棵,则所求的概率大约为==0.2.
(2)树苗的平均高度x≈
=
=73.8厘米.
(3)依题意,记[40,50)组中的树苗分别为A、B,[90,100]组中的树苗分别为C、D、E、F,则所有的基本事件为2·1·c·n·j·y
ACD、ACE、ACF、ADE、ADF、AEF、BCD、BCE、BCF、BDE、BDF、BEF,共12个.【来源:21cnj*y.co*m】
满足A、C同时被移出的基本事件为ACD、ACE、ACF,共3个,所以树苗A和树苗C同时被移出的概率P==0.25.
22.(12分)已知关于x的二次函数f ( http: / / www.21cnjy.com )(x)=ax2-bx+1(a≠0),设集合P={1,2,3},Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数a和b得到的数对(a,b).【来源:21·世纪·教育·网】
(1)列举出所有的数对(a,b),并求函数y=f(x)有零点的概率;
(2)求函数y=f(x)在区间[1,+∞)上是增函数的概率.
解 (1)(a,b)共有(1,-1), ( http: / / www.21cnjy.com )(1,1),(1,2),(1,3),(1,4),(2,-1),(2,1),(2,2),(2,3),(2,4),(3,-1),(3,1),(3,2),(3,3),(3,4),15种情况.21*cnjy*com
函数y=f(x)有零点,Δ=b2-4a≥0,
有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共6种情况
所以函数y=f(x)有零点的概率为=.
(2)函数y=f(x)的对称轴为x=,
在区间[1,+∞)上是增函数,则有≤1,即b-2a≤0.
因此有(1,-1),(1,1),(1,2 ( http: / / www.21cnjy.com )),(2,-1),(2,1),(2,2),(2,3),(2,4),(3,-1),(3,1),(3,2),(3,3),(3,4),共13种情况满足条件,
所以函数y=f(x)在区间[1,+∞)上是增函数的概率为.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第三章测试
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的)
1.先后抛掷2枚一分、二分的硬币,观察落地后硬币的正、反面情况,则下列事件包含3个基本事件的是( )21世纪教育网版权所有
A.至少一枚硬币正面向上
B.只有一枚硬币正面向上
C.两枚硬币都是正面向上
D.两枚硬币一枚正面向上,另一枚正面向下
解析 先后抛掷2枚一分、二分的硬币,其结 ( http: / / www.21cnjy.com )果有4种情形:“1正2正”、“1正2反”、“1反2正”、“1反2反”,可得“至少一枚硬币正面向上”包含3个基本事件. 21*cnjy*com
答案 A
2.下列命题:
①对立事件一定是互斥事件;②若A,B为两个 ( http: / / www.21cnjy.com )随机事件,则P(A∪B)=P(A)+P(B);③若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A,B满足P(A)+P(B)=1,则A与B是对立事件.
其中正确命题的个数是( )
A.1 B.2
C.3 D.4
解析 ①正确;②不正确,当A与B是互斥事件 ( http: / / www.21cnjy.com )时,才有P(A∪B)=P(A)+P(B),对于任意两个事件A,B满足P(A∪B)=P(A)+P(B)-P(AB);③也不正确.P(A)+P(B)+P(C)不一定等于1,还可能小于1;④也不正确.例如:袋中有大小相同的红、黄、黑、绿4个球,从袋中任摸一个球,设事件A={摸到红球或黄球},事件B={摸到黄球或黑球},显然事件A与B不互斥,但P(A)+P(B)=+=1.
答案 A
3.掷一枚均匀的硬币,如果连续抛掷1000次,那么第999次出现正面向上的概率是( )
A. B.
C. D.
解析 投掷一枚均匀的硬币正面向上的概率为,它不因抛掷的次数而变化,因此抛掷一次正面向上的概率为,抛掷第999次正面向上的概率还是.【出处:21教育名师】
答案 D
4.某导演先从2个金鸡奖和 ( http: / / www.21cnjy.com )3个百花奖的5位演员名单中挑选2名演主角,后又从剩下的演员中挑选1名演配角.这位导演挑选出2个金鸡奖演员和1个百花奖演员的概率为( )
A. B.
C. D.
解析 设2个金鸡奖演员编号为1,2,3 ( http: / / www.21cnjy.com )个百花奖演员编号为3,4,5.从编号为1,2,3,4,5的演员中任选3名有10种挑选方法:(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),其中挑选出2名金鸡奖和1名百花奖的有3种:(1,2,3),(1,2,4),(1,2,5),故所求的概率为P=.
答案 D
5.设某厂产品的次品率为3%,估计该厂8000件产品中次品的件数为( )
A.3 B.160
C.240 D.7480
解析 次品数为8000×3%=240.
答案 C
6.有四个游戏盘,将它们水平放稳后,在上面扔一颗小玻璃球,若小球落在阴影部分,则可中奖,小明要想增加中奖机会,应选择的游戏盘是( )
解析 由几何概型概率公式知,图中中 ( http: / / www.21cnjy.com )奖的概率依次是P(A)=,P(B)=,P(C)==,P(D)=,因此,要想增加中奖机会,应选择A盘.
答案 A
7.在线段AB上任取三个点x1,x2,x3,则x2位于x1与x3之间的概率为( )
A. B.
C. D.1
解析 由于x1,x2,x3是任意的 ( http: / / www.21cnjy.com ),它们的排列次序有:x1x2x3,x2x1x3,x2x3x1,x3x2x1,x1x3x2,x3x1x2,共6种情况.其中x2在x1与x3之间有两种情况,故所求概率为=.
答案 B
8.小明同学的QQ密码是由0,1,2,3,4 ( http: / / www.21cnjy.com ),5,6,7,8,9这10个数字中的6个数字组成的六位数,由于长时间未登录QQ,小明忘记了密码的最后一个数字,如果小明登录QQ时密码的最后一个数字随意选取,则恰好能登录的概率是( )21·cn·jy·com
A. B.
C. D.
解析 只考虑最后一位数字即可,从0至9这10个数字中任取一个,作为密码的最后一位数字有10种可能,其中只有一种可能登录成功,故其概率为.
答案 D
9.某人从甲地去乙地共走了 ( http: / / www.21cnjy.com )500 m,途中要过一条宽为x m的河流,他不小心把一件物品丢在途中,若物品掉在河里就找不到,若物品不掉在河里,则能找到,已知该物品能找到的概率为,则河宽为( )
A.100 m B.80 m
C. 50 m D.40 m
解析 设河宽x m,则1-=,∴x=100 (m).
答案 A
10.如图的矩形长为5、宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分的面积为( )
A. B.
C. 10 D.不能估计
解析 利用几何概型的概率计算公式,得阴影部分的面积约为×(5×2)=.
答案 A
11.在所有的两位数(10~99)中,任取一个数,则这个数能被2或3整除的概率是( )
A. B.
C. D.
解析 在10~99中有9 ( http: / / www.21cnjy.com )9-10+1=90个整数,其中能被2整除的有45个,能被3整除的有30个,能被6整除的有15个,因此,所求的概率为P==.21cnjy.com
答案 C
12.小丽和小明一起用A,B两枚均匀的 ( http: / / www.21cnjy.com )小正方体(立方体的每个面上分别标有数字1,2,3,4,5,6)玩游戏,以小丽掷出的A立方体朝上的数字为x,小明掷出的B立方体朝上的数字为y,来确定点P(x,y),那么他们各掷一次所确定的点P(x,y)落在抛物线y=-x2+4x上的概率为( )
A. B.
C. D.
解析 根据题意,两人各掷小正方体一次, ( http: / / www.21cnjy.com )每人都有6种可能性,则点P(x,y)的情况有6×6=36种可能,而y=-x2+4x=-(x-2)2+4,即(x-2)2+y=4,易得在抛物线上的点有(2,4),(1,3),(3,3)共3种.因此满足条件的概率为=.
答案 C
二、填空题(本大题共4小题,每小题5分,满分20分.把答案填在题中横线上)
13.一种投掷骰子的游戏规则是:交 ( http: / / www.21cnjy.com )2元钱可掷一次骰子,若骰子朝上的点数是1,则中奖2元;若点数是2或3,则中奖1元,若点数是4,5或6,则无奖,某人投掷一次,那么中奖的概率是______.
解析 由题意知,投掷一次骰子若点数为1,2,3则获奖,若出现点数4,5,6无奖,所以中奖的概率为.
答案
14.设集合A={0,1,2},B={0 ( http: / / www.21cnjy.com ),1,2},分别从集合A和B中随机取一个数a和b,确定平面上一个点P(a,b),设“点P(a,b)落在直线x+y=n上”为事件Cn(0≤n≤4,n∈N),若事件Cn的概率最大,则n的可能值为________.【版权所有:21教育】
解析 基本事件为点(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),总数为9.www.21-cn-jy.com
当n=0时,落在直线x+y=0上的点有1个(0,0);
当n=1时,落在直线x+y=1上的点有2个,(0,1)和(1,0);
当n=2时,落在直线x+y=2上的点有(1,1),(2,0),(0,2),共3个;
当n=3时,落在直线x+y=3上的点有(1,2),(2,1)共2个;
当n=4时,落在直线x+y=4上的点只有(2,2)1个.
因此,当Cn的概率最大时,n=2.
答案 2
15.已知区域E={(x,y)|0≤ ( http: / / www.21cnjy.com )x≤3,0≤y≤2},F={(x,y)|0≤x≤3,0≤y≤2,x≥y},若向区域E内随机投掷一点,则该点落入区域F内的概率为________.21·世纪*教育网
解析 依题意可知,本问题属于几何概型,区域E和区域F的对应图形如图所示.
其中区域E的面积为3×2=6,区域F的面积为×(1+3)×2=4,所以向区域E内随机投掷一点,该点落入区域F内的概率为P==.
答案
16.从4名男生和2名女生中任选3人参加演讲比赛,所选3人中至少有1名女生的概率为,那么所选3人中都是男生的概率为________.www-2-1-cnjy-com
解析 设A={3人中至少有1名女生},B={3人中都是男生},则A,B为对立事件,∴P(B)=1-P(A)=.2-1-c-n-j-y
答案
三、解答题(本大题共6小题,满分70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)某学校篮球队,羽毛球队、乒乓球队各有10名队员,某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求:21教育名师原创作品
(1)该队员只属于一支球队的概率;
(2)该队员最多属于两支球队的概率.
解 由图知,三支球队共有队员10+4+3+3=20人,其中只参加一支球队的队员有5+4+3=12人,参加两支球队的队员有1+2+3=6人.
(1)设“该队员只属于一支球队”为事件A,
则P(A)==.
(2)设“该队员最多属于两支球队”为事件B,
则P(B)=+==.(或P(B)=1-=)
18.(12分)高一军训时,某同学射击一次,命中10环,9环,8环的概率分别为0.13,0.28,0.31.
(1)求射击一次,命中10环或9环的概率;
(2)求射击一次,至少命中8环的概率;
(3)求射击一次,命中环数小于9环的概率.
解 设事件“射击一次,命中i环”为事件 ( http: / / www.21cnjy.com )Ai(0≤i≤10,且i∈N),且Ai两两互斥.由题意知P(A10)=0.13,P(A9)=0.28,P(A8)=0.31.
(1)记“射击一次,命中10环或9环”的事件为A,那么P(A)=P(A10)+P(A9)=0.13+0.28=0.41.
(2)记“射击一次,至少命中8环”的事件为B,那么P(B)=P(A10)+P(A9)+P(A8)=0.13+0.28+0.31=0.72.
(3)记“射击一次,命中环数小于9环”的事件为C,则C与A是对立事件,∴P(C)=1-P(A)=1-0.41=0.59.
19.(12分)水池的容积是2 ( http: / / www.21cnjy.com )0 m3,向水池注水的水龙头A和水龙头B的流速都是1 m3/h,它们在一昼夜内随机开放(0~24小时),求水池不溢出水的概率.(精确到0.01)
解 设水龙头A开x小时,水龙头B开y小时,若水池不溢出水,则x+y≤20,
记“水池不溢出水”为事件M,则M所占区 ( http: / / www.21cnjy.com )域面积为×20×20=200,整个区域的面积为24×24=576,由几何概型的概率公式,得P(M)=≈0.35,
即水池不溢出水的概率为0.35.
20.(12分)A、B两个箱子分别装有标号为0,1,2的三种卡片,每种卡片的张数如表所示.
( http: / / www.21cnjy.com )
(1)从A、B箱中各取1张卡片,用x表示取出的2张卡片的数字之积,求x=2的概率;
(2)从A、B箱中各取1张卡片,用y表示取出的2张卡片的数字之和,求x=0,y=2的概率.
解 依题意知,从A、B箱中各取1张卡片,其基本事件有6×5=30个.
(1)记事件C为“从A、B箱中各取1张卡片,2张卡片的数字之积等于2”,则C包含5个基本事件,由古典概型的概率公式得P(C)==.
(2)记事件D为“从A、B箱中各取1张卡片,其数字之和为2且积为0”,则包含10个基本事件,则P(D)==.
21.(12分)某中学生物兴趣小组在学校生 ( http: / / www.21cnjy.com )物园地种植了一批名贵树苗,为了解树苗生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米).把这些高度列成了如下的频数分布表:
组别 [40,50) [50,60) [60,70) [70,80) [80,90) [90,100]
频数 2 3 14 15 12 4
(1)在这批树苗中任取一棵,其高度在85厘米以上的概率大约是多少?
(2)这批树苗的平均高度大约是多少?(计算时可以用组中值代替各组数据的平均值)
(3)为了进一步获得研究资料 ( http: / / www.21cnjy.com ),若从[40,50)组中移出一棵树苗,从[90,100]组中移出两棵树苗进行试验研究,则[40,50)组中的树苗A和[90,100]组中的树苗C同时被移出的概率是多少?21教育网
解 (1)由已知,高度在85厘米以上的树苗大约有6+4=10棵,则所求的概率大约为==0.2.
(2)树苗的平均高度x≈
=
=73.8厘米.
(3)依题意,记[40,50)组中的树苗分别为A、B,[90,100]组中的树苗分别为C、D、E、F,则所有的基本事件为2·1·c·n·j·y
ACD、ACE、ACF、ADE、ADF、AEF、BCD、BCE、BCF、BDE、BDF、BEF,共12个.【来源:21cnj*y.co*m】
满足A、C同时被移出的基本事件为ACD、ACE、ACF,共3个,所以树苗A和树苗C同时被移出的概率P==0.25.
22.(12分)已知关于x的二次函数f ( http: / / www.21cnjy.com )(x)=ax2-bx+1(a≠0),设集合P={1,2,3},Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数a和b得到的数对(a,b).【来源:21·世纪·教育·网】
(1)列举出所有的数对(a,b),并求函数y=f(x)有零点的概率;
(2)求函数y=f(x)在区间[1,+∞)上是增函数的概率.
解 (1)(a,b)共有(1,-1), ( http: / / www.21cnjy.com )(1,1),(1,2),(1,3),(1,4),(2,-1),(2,1),(2,2),(2,3),(2,4),(3,-1),(3,1),(3,2),(3,3),(3,4),15种情况.21*cnjy*com
函数y=f(x)有零点,Δ=b2-4a≥0,
有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共6种情况
所以函数y=f(x)有零点的概率为=.
(2)函数y=f(x)的对称轴为x=,
在区间[1,+∞)上是增函数,则有≤1,即b-2a≤0.
因此有(1,-1),(1,1),(1,2 ( http: / / www.21cnjy.com )),(2,-1),(2,1),(2,2),(2,3),(2,4),(3,-1),(3,1),(3,2),(3,3),(3,4),共13种情况满足条件,
所以函数y=f(x)在区间[1,+∞)上是增函数的概率为.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
