【名师一号】2014-2015学年新课标A版高中数学必修5:第三章+不等式++单元同步测试(含解析)
文档属性
| 名称 | 【名师一号】2014-2015学年新课标A版高中数学必修5:第三章+不等式++单元同步测试(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 34.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-08 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第三章测试
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若<<0,则下列不等式中不正确的是( )
A.a+b2
C.ab解析 由<<0,可得b答案 D
2.若a,b>0,且P=,Q=,则P,Q的大小关系是( )
A.P>Q B.PC.P≥Q D.P≤Q
解析 P2-Q2=-(a+b)
=≤0,
所以P2≤Q2,即P≤Q.
答案 D
3.已知向量a=(x,-1),b=(y-1,1),x,y∈R+,若a∥b,则t=x++y+的最小值是( )2-1-c-n-j-y
A.4 B.5
C.6 D.8
解析 由a∥b,得x+y=1.
∴t=t(x+y)=(x+y)=1+1+++1≥3+2=5.
当且仅当x=y=时,t取最小值5.
答案 B
4.若集合A={x|(2x+1)(x-3)<0},B={x∈N*|x≤5},则A∩B是( )
A.{1,2,3} B.{1,2}
C.{4,5} D.{1,2,3,4,5}
解析 因为集合A={x|-答案 B
5.若mA.pC.p解析 将p,q看成变量,则m答案 B
6.当点(x,y)在直线x+3y=2上移动时,z=3x+27y+1的最小值是( )
A.3 B.7
C.1+2 D.6
解析 z=3x+27y+1≥2+1=2+1=2+1=7.
答案 B
7.
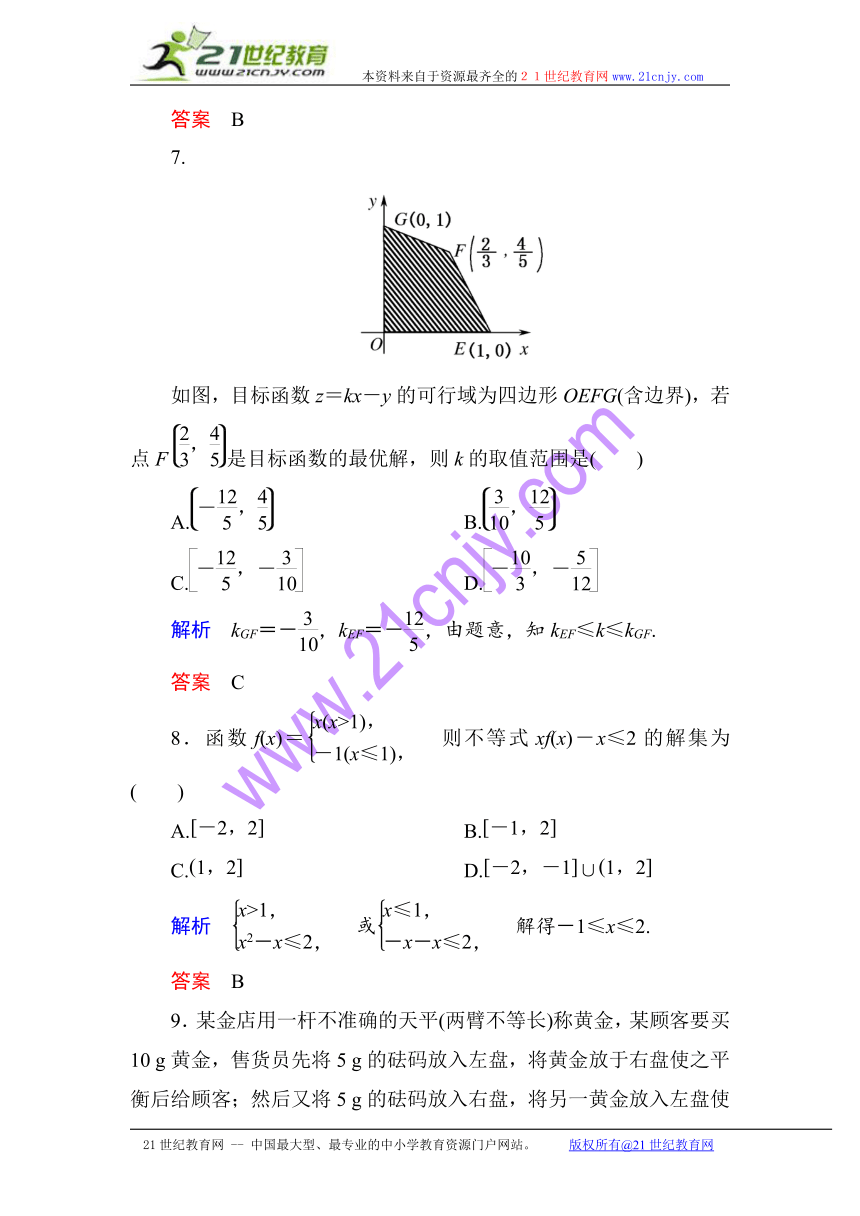
如图,目标函数z=kx-y的可行域为四边形OEFG(含边界),若点F是目标函数的最优解,则k的取值范围是( )
A. B.
C. D.
解析 kGF=-,kEF=-,由题意,知kEF≤k≤kGF.
答案 C
8.函数f(x)=则不等式xf(x)-x≤2的解集为( )
A. B.
C. D.∪
解析 或解得-1≤x≤2.
答案 B
9.某金店用一杆不准确的天平(两臂不等长 ( http: / / www.21cnjy.com ))称黄金,某顾客要买10 g黄金,售货员先将5 g的砝码放入左盘,将黄金放于右盘使之平衡后给顾客;然后又将5 g的砝码放入右盘,将另一黄金放入左盘使之平衡后又给顾客,则顾客实际所得黄金( )21世纪教育网版权所有
A.大于10 g B.小于10 g
C.大于等于10 g D.小于等于10 g
解析 设天平的两边臂长分别为a,b,两次所称黄金的重量分别为xg,yg.
则所以x+y=+>2 =10.
答案 A
10.对任意的a∈,函数f(x)=x2+(a-4)x+4-2a的值总大于0,则x的取值范围为( )2·1·c·n·j·y
A.(1,3) B.(-∞,1)∪(3,+∞)
C.(-∞,1) D.(3,+∞)
解析 y=φ(a)=(x-2)a+(x2-4x+4),
x=2时,y=0,所以x≠2.只需
答案 B
11.设a>0,b>0,若是3a与3b的等比中项,则+的最小值为( )
A.8 B.4
C.1 D.
解析 ∵a>0,b>0,3a·3b=3,∴a+b=1,
∴+=+=1+++1≥2+2 =4.
答案 B
12.对于使-x2+2x≤m成立的所有常数 ( http: / / www.21cnjy.com )M中,我们把M的最小值叫做-x2+2x的上确界.若a,b∈R+,且a+b=1,则--的上确界为( )21cnjy.com
A.-3 B.-4
C.- D.-
解析 ∵a,b∈R+,且a+b=1,
∴+=+=+++2≥+2 =,∴--≤-,即--的上确界为-.
答案 D
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.设a>b,则①ac2>bc2;②2a>2b;③<;④a3>b3;⑤|a|>|b|.正确的结论有________.21教育网
答案 ②④
14.函数y=2x2+的最小值是________.
解析 y=2x2+=2(x2+1)+-2≥2-2=2×4-2=6.
当且仅当2(x2+1)=.即x=±1时,等号成立.
答案 6
15.已知不等式x2-ax-b<0的解集为(2,3),则不等式bx2-ax-1>0的解集为________.21·世纪*教育网
解析 依题意知方程x2-ax-b=0的两根 ( http: / / www.21cnjy.com )为2,3,根据韦达定理可求得a=5,b=-6,所以不等式为6x2+5x+1<0,解得-答案
16.某实验室需购某种化工 ( http: / / www.21cnjy.com )原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元.在满足需要的条件下,最少要花费________元.
解析 设购买35kg的x袋,24kg的 ( http: / / www.21cnjy.com )y袋,则35x+24y≥106,x∈N,y∈N,共花费z=140x+120y,作出由对应的平面区域,则知目标函数在(1,3)点处取得最小值为500元.
答案 500
三、解答题(本大题共6个小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)已知a,b,x,y>0且>,x>y,
求证:>.
证明:-=.
由>>0,可得b>a>0.
又∵x>y>0,∴bx>ay,x+a>0,y+b>0,
∴>0,∴>.
18.(12分)设f(x)=(m+1)x2-mx+m-1.
(1)当m=1时,求不等式f(x)>0的解集;
(2)若不等式f(x)+1>0的解集为(,3),求m的值.
解 (1)当m=1时,f(x)>0,即
2x2-x>0 x(2x-1)>0 x<0,或x>.
∴此时不等式的解集为(-∞,0)∪(,+∞).
(2)由f(x)+1>0,得(m+1)x2-mx+m>0.
∵不等式的解集为(,3),
∴和3是方程(m+1)x2-mx+m=0的两个根,
且m+1<0.
∴解得m=-.
19.(12分)已知关于x的不等式kx2-2x+6k<0(k≠0).
(1)若不等式的解集是{x|x<-3或x>-2},求k的值;
(2)若不等式的解集为R,求k的取值范围.
解 (1)∵不等式kx2-2x+6k<0的解集是{x|x<-3或x>-2},
∴方程kx2-2x+6k=0的两根为-3,-2,且k<0.
由根与系数的关系得∴k=-.
(2)∵不等式kx2-2x+6k<0的解集为R,
∴解得
故k的取值范围是.
20.(12分)某校伙食长期以面粉 ( http: / / www.21cnjy.com )和大米为主食,面食每100 g含蛋白质6个单位,含淀粉4个单位,售价0.5元,米食每100 g含蛋白质3个单位,含淀粉7个单位,售价0.4元,学校要求给学生配制盒饭,每盒盒饭至少有8个单位的蛋白质和10个单位的淀粉,问应如何配制盒饭,才既科学又费用最少?21·cn·jy·com
解 设每盒盒饭需要面食x百克,米食y百克,所需费用为z=0.5x+0.4y,且x,y满足
作出可行域,如图所示.由图可知,平行直线系y=-x+z过点A时,纵截距z最小,即z最小.由解得点A.【来源:21·世纪·教育·网】
所以每盒盒饭为面食百克,米食百克时,既科学又费用最少.
21.(12分)若f(x)是定义在 ( http: / / www.21cnjy.com )(0,+∞)上的增函数,且对一切x>0,y>0满足f=f(x)-f(y),若f(2)=1,解不等式f(x+3)-f<2.
解 由f(x+3)-f<2,得
即
又f=f(4)-f(2),∴f(4)=2f(2)=2.
∴
∵f(x)是(0,+∞)上的增函数,
∴解得022.(12分)某渔业公司今年初用98万元购 ( http: / / www.21cnjy.com )进一艘渔船用于捕捞,第一年需各种费用12万元,从第二年开始包括维修费在内,每年所需费用均比上一年增加4万元,该船每年捕捞的总收入为50万元.
(1)该船捕捞几年开始盈利?(即总收入减去成本及所有费用之差为正值)
(2)该船捕捞若干年后,处理方案有两种:
①当年平均盈利达到最大值时,以26万元的价格卖出;
②当盈利总额达到最大值时,以8万元的价格卖出.问哪一种方案较为合算,请说明理由.
解 (1)设捕捞n年后开始盈利,盈利为y元,则y=50n--98=-2n2+40n-98.
由y>0,得n2-20n+49<0,
解得10-则3≤n≤17,故n=3.即捕捞3年后,开始盈利.
(2)①平均盈利为=-2n-+40≤-2+40=12,当且仅当2n=,即n=7时,年平均盈利最大.www-2-1-cnjy-com
故经过7年捕捞后年平均盈利最大,共盈利12×7+26=110万元.
②∵y=-2n2+40n-98=-2(n-10)2+102,
∴当n=10时,y的最大值为102.
即经过10年捕捞盈利总额最大,共盈利102+8=110万元.
综上知两种方案获利相等,但方案②的时间长,所以方案①合算.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第三章测试
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若<<0,则下列不等式中不正确的是( )
A.a+b
C.ab
2.若a,b>0,且P=,Q=,则P,Q的大小关系是( )
A.P>Q B.P
解析 P2-Q2=-(a+b)
=≤0,
所以P2≤Q2,即P≤Q.
答案 D
3.已知向量a=(x,-1),b=(y-1,1),x,y∈R+,若a∥b,则t=x++y+的最小值是( )2-1-c-n-j-y
A.4 B.5
C.6 D.8
解析 由a∥b,得x+y=1.
∴t=t(x+y)=(x+y)=1+1+++1≥3+2=5.
当且仅当x=y=时,t取最小值5.
答案 B
4.若集合A={x|(2x+1)(x-3)<0},B={x∈N*|x≤5},则A∩B是( )
A.{1,2,3} B.{1,2}
C.{4,5} D.{1,2,3,4,5}
解析 因为集合A={x|-
5.若m
6.当点(x,y)在直线x+3y=2上移动时,z=3x+27y+1的最小值是( )
A.3 B.7
C.1+2 D.6
解析 z=3x+27y+1≥2+1=2+1=2+1=7.
答案 B
7.
如图,目标函数z=kx-y的可行域为四边形OEFG(含边界),若点F是目标函数的最优解,则k的取值范围是( )
A. B.
C. D.
解析 kGF=-,kEF=-,由题意,知kEF≤k≤kGF.
答案 C
8.函数f(x)=则不等式xf(x)-x≤2的解集为( )
A. B.
C. D.∪
解析 或解得-1≤x≤2.
答案 B
9.某金店用一杆不准确的天平(两臂不等长 ( http: / / www.21cnjy.com ))称黄金,某顾客要买10 g黄金,售货员先将5 g的砝码放入左盘,将黄金放于右盘使之平衡后给顾客;然后又将5 g的砝码放入右盘,将另一黄金放入左盘使之平衡后又给顾客,则顾客实际所得黄金( )21世纪教育网版权所有
A.大于10 g B.小于10 g
C.大于等于10 g D.小于等于10 g
解析 设天平的两边臂长分别为a,b,两次所称黄金的重量分别为xg,yg.
则所以x+y=+>2 =10.
答案 A
10.对任意的a∈,函数f(x)=x2+(a-4)x+4-2a的值总大于0,则x的取值范围为( )2·1·c·n·j·y
A.(1,3) B.(-∞,1)∪(3,+∞)
C.(-∞,1) D.(3,+∞)
解析 y=φ(a)=(x-2)a+(x2-4x+4),
x=2时,y=0,所以x≠2.只需
答案 B
11.设a>0,b>0,若是3a与3b的等比中项,则+的最小值为( )
A.8 B.4
C.1 D.
解析 ∵a>0,b>0,3a·3b=3,∴a+b=1,
∴+=+=1+++1≥2+2 =4.
答案 B
12.对于使-x2+2x≤m成立的所有常数 ( http: / / www.21cnjy.com )M中,我们把M的最小值叫做-x2+2x的上确界.若a,b∈R+,且a+b=1,则--的上确界为( )21cnjy.com
A.-3 B.-4
C.- D.-
解析 ∵a,b∈R+,且a+b=1,
∴+=+=+++2≥+2 =,∴--≤-,即--的上确界为-.
答案 D
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.设a>b,则①ac2>bc2;②2a>2b;③<;④a3>b3;⑤|a|>|b|.正确的结论有________.21教育网
答案 ②④
14.函数y=2x2+的最小值是________.
解析 y=2x2+=2(x2+1)+-2≥2-2=2×4-2=6.
当且仅当2(x2+1)=.即x=±1时,等号成立.
答案 6
15.已知不等式x2-ax-b<0的解集为(2,3),则不等式bx2-ax-1>0的解集为________.21·世纪*教育网
解析 依题意知方程x2-ax-b=0的两根 ( http: / / www.21cnjy.com )为2,3,根据韦达定理可求得a=5,b=-6,所以不等式为6x2+5x+1<0,解得-
16.某实验室需购某种化工 ( http: / / www.21cnjy.com )原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元.在满足需要的条件下,最少要花费________元.
解析 设购买35kg的x袋,24kg的 ( http: / / www.21cnjy.com )y袋,则35x+24y≥106,x∈N,y∈N,共花费z=140x+120y,作出由对应的平面区域,则知目标函数在(1,3)点处取得最小值为500元.
答案 500
三、解答题(本大题共6个小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)已知a,b,x,y>0且>,x>y,
求证:>.
证明:-=.
由>>0,可得b>a>0.
又∵x>y>0,∴bx>ay,x+a>0,y+b>0,
∴>0,∴>.
18.(12分)设f(x)=(m+1)x2-mx+m-1.
(1)当m=1时,求不等式f(x)>0的解集;
(2)若不等式f(x)+1>0的解集为(,3),求m的值.
解 (1)当m=1时,f(x)>0,即
2x2-x>0 x(2x-1)>0 x<0,或x>.
∴此时不等式的解集为(-∞,0)∪(,+∞).
(2)由f(x)+1>0,得(m+1)x2-mx+m>0.
∵不等式的解集为(,3),
∴和3是方程(m+1)x2-mx+m=0的两个根,
且m+1<0.
∴解得m=-.
19.(12分)已知关于x的不等式kx2-2x+6k<0(k≠0).
(1)若不等式的解集是{x|x<-3或x>-2},求k的值;
(2)若不等式的解集为R,求k的取值范围.
解 (1)∵不等式kx2-2x+6k<0的解集是{x|x<-3或x>-2},
∴方程kx2-2x+6k=0的两根为-3,-2,且k<0.
由根与系数的关系得∴k=-.
(2)∵不等式kx2-2x+6k<0的解集为R,
∴解得
故k的取值范围是.
20.(12分)某校伙食长期以面粉 ( http: / / www.21cnjy.com )和大米为主食,面食每100 g含蛋白质6个单位,含淀粉4个单位,售价0.5元,米食每100 g含蛋白质3个单位,含淀粉7个单位,售价0.4元,学校要求给学生配制盒饭,每盒盒饭至少有8个单位的蛋白质和10个单位的淀粉,问应如何配制盒饭,才既科学又费用最少?21·cn·jy·com
解 设每盒盒饭需要面食x百克,米食y百克,所需费用为z=0.5x+0.4y,且x,y满足
作出可行域,如图所示.由图可知,平行直线系y=-x+z过点A时,纵截距z最小,即z最小.由解得点A.【来源:21·世纪·教育·网】
所以每盒盒饭为面食百克,米食百克时,既科学又费用最少.
21.(12分)若f(x)是定义在 ( http: / / www.21cnjy.com )(0,+∞)上的增函数,且对一切x>0,y>0满足f=f(x)-f(y),若f(2)=1,解不等式f(x+3)-f<2.
解 由f(x+3)-f<2,得
即
又f=f(4)-f(2),∴f(4)=2f(2)=2.
∴
∵f(x)是(0,+∞)上的增函数,
∴解得0
(1)该船捕捞几年开始盈利?(即总收入减去成本及所有费用之差为正值)
(2)该船捕捞若干年后,处理方案有两种:
①当年平均盈利达到最大值时,以26万元的价格卖出;
②当盈利总额达到最大值时,以8万元的价格卖出.问哪一种方案较为合算,请说明理由.
解 (1)设捕捞n年后开始盈利,盈利为y元,则y=50n--98=-2n2+40n-98.
由y>0,得n2-20n+49<0,
解得10-
(2)①平均盈利为=-2n-+40≤-2+40=12,当且仅当2n=,即n=7时,年平均盈利最大.www-2-1-cnjy-com
故经过7年捕捞后年平均盈利最大,共盈利12×7+26=110万元.
②∵y=-2n2+40n-98=-2(n-10)2+102,
∴当n=10时,y的最大值为102.
即经过10年捕捞盈利总额最大,共盈利102+8=110万元.
综上知两种方案获利相等,但方案②的时间长,所以方案①合算.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
