【名师一号】2014-2015学年新课标A版高中数学选修2-1:第三章++空间向量与立体几何+单元同步测试(含解析)
文档属性
| 名称 | 【名师一号】2014-2015学年新课标A版高中数学选修2-1:第三章++空间向量与立体几何+单元同步测试(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 105.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-09 11:11:53 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第三章测试
(时间:120分钟,满分:150分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的)
1.向量a=(2x,1,3),b=(1,-2y,9),若a与b共线,则( )
A.x=1,y=1 B.x=,y=-
C.x=,y=- D.x=-,y=
解析 由a∥b知,a=λb,∴2x=λ,1=-2λy,3=9λ,∴λ=,x=,y=-.
答案 C
2.已知a=(-3,2,5),b=(1,x,-1),且a·b=2,则x的值是( )
A.6 B.5
C.4 D.3
解析 a·b=-3+2x-5=2,∴x=5.
答案 B
3.设l1的方向向量为a=(1,2,-2),l2的方向向量为b=(-2,3,m),若l1⊥l2,则实数m的值为( )2-1-c-n-j-y
A.3 B.2
C.1 D.
解析 ∵l1⊥l2,∴a⊥b,∴a·b=0,∴-2+6-2m=0,∴m=2.
答案 B
4.若a,b均为非零向量,则a·b=|a||b|是a与b共线的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
解析 ∵a·b=|a||b|cos〈a,b〉,而a·b=|a||b|.
∴cos〈a,b〉=1,∴〈a,b〉=0.
∴a与b共线.反之,若a与b共线,也可能a·b=-|a|·|b|,因此应选B.
答案 B
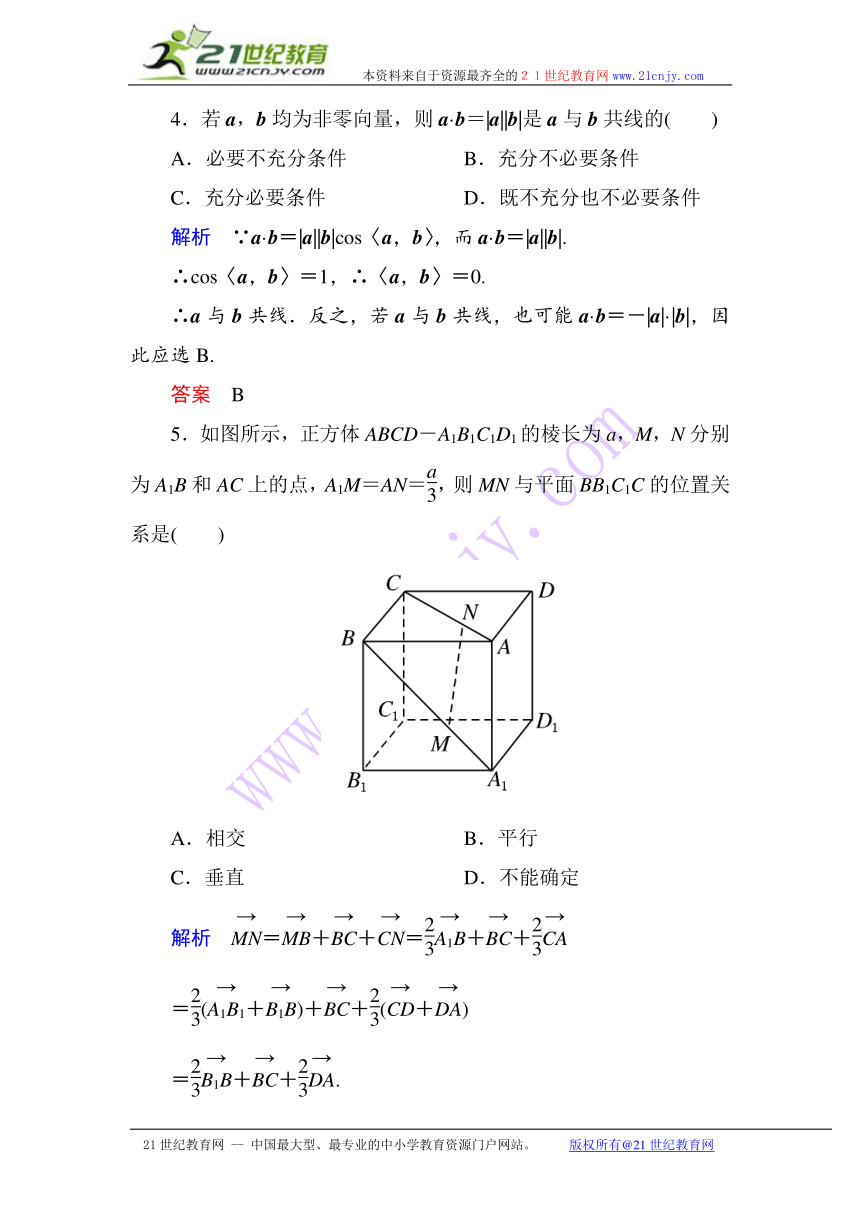
5.如图所示,正方体ABCD-A1B1C ( http: / / www.21cnjy.com )1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是( )2·1·c·n·j·y
A.相交 B.平行
C.垂直 D.不能确定
解析 =++=++
=(+)++(+)
=++.
而是平面BB1C1C的一个法向量,且·=·=0,
∴⊥.
又MN 平面BB1C1C,∴MN∥平面BB1C1C.
答案 B
6.已知a,b,c是空间的一个基底,设p=a+b,q=a-b,则下列向量中可以与p,q一起构成空间的另一个基底的是( )
A.a B.b
C.c D.以上都不对
解析 ∵a,b,c不共面,
∴a+b,a-b,c不共面,∴p,q,c可构成空间的一个基底.
答案 C
7.已知△ABC的三个顶点A(3,3,2),B(4,-3,7),C(0,5,1),则BC边上的中线长为( ) 21*cnjy*com
A.2 B.3
C. D.
解析 BC的中点D的坐标为(2,1,4),
∴=(-1,-2,2).
∴||==3.
答案 B
8.与向量a=(2,3,6)共线的单位向量是( )
A.(,,)
B.(-,-,-)
C.(,-,-)和(-,,)
D.(,,)和(-,-,-)
解析 |a|==7,∴与a共线的单位向量是±(2,3,6),故应选D.
答案 D
9.已知向量a=(2,4,x),b=(2,y,2),若|a|=6且a⊥b,则x+y为( )
A.-3或1 B.3或-1
C.-3 D.1
解析 由|a|=6,a⊥b,
得解得或
∴x+y=1,或-3.
答案 A
10.已知a=(x,2,0),b=(3,2-x,x2),且a与b的夹角为钝角,则实数x的取值范围是( )21教育网
A.x>4 B.x<-4
C.0解析 ∵〈a,b〉为钝角,∴a·b=|a||b|cos〈a,b〉<0,即3x+2(2-x)<0,∴x<-4.21cnjy.com
答案 B
11.已知空间四个点A(1,1,1),B( ( http: / / www.21cnjy.com )-4,0,2),C(-3,-1,0),D(-1,0,4),则直线AD与平面ABC所成的角为( )www.21-cn-jy.com
A.30° B.45°
C.60° D.90°
解析 设平面ABC的一个法向量为n=(x,y,z),
∵=(-5,-1,1),=(-4,-2,-1),
由n·=0及n·=0,得
令z=1,
得x=,y=-,∴n=(,-,1).
又=(-2,-1,3),设AD与平面ABC所成的角为θ,则
sinθ===,
∴θ=30°.
答案 A
12.如图所示,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )
A. B.
C. D.
解析 不妨令CB=1,则CA=CC1=2,得O(0,0,0),B(0,0,1),C1(0,2,0),A(2,0,0),B1(0,2,1),21·cn·jy·com
∴=(0,2,-1),=(-2,2,1).
∴cos〈,〉===.
答案 A
二、填空题(本大题共4小题,每小题5分,满分20分.把答案填在题中横线上)
13.已知{i,j,k}为单位正交基底,且 ( http: / / www.21cnjy.com )a=-i+j+3k,b=2i-3j-2k,则向量a+b与向量a-2b的坐标分别是________;________.
解析 依题意知,a=(-1,1,3),b=(2,-3,-2),则a+b=(1,-2,1),
a-2b=(-1,1,3)-2(2,-3,-2)=(-5,7,7).
答案 (1,-2,1) (-5,7,7)
14.在△ABC中,已知=(2,4,0),=(-1,3,0),则∠ABC=________.
解析 cos〈,〉===,
∴〈,〉=,∴∠ABC=π-=.
答案
15.正方体ABCD-A1B1C1D1中,面ABD1与面B1BD1所夹角的大小为________.
解析
建立空间直角坐标系D-xyz,如图.
设正方体的棱长为1,则A(1,0,0),B(1,1,0),B1(1,1,1),D1(0,0,1).
∴=(1,0,-1),=(1,1,-1),=(1,1,0).
设平面ABD1的法向量为m ( http: / / www.21cnjy.com )=(x1,y1,z1),平面B1BD1的法向量为n=(x2,y2,z2),则由m·=0,m·=0,可得m=(1,0,1),由n·=0,n·=0,得n=(1,-1,0),∴cos〈m,n〉==.∴所求二平面的大小为60°.21世纪教育网版权所有
答案 60°
16.在下列命题中:①若a,b共线,则 ( http: / / www.21cnjy.com )a,b所在的直线平行;②若a,b所在的直线是异面直线,则a,b一定不共面;③若a,b,c三向量两两共面,则a,b,c三向量一定也共面;④已知三向量a,b,c,则空间任意一个向量p总可以唯一表示为p=xa+yb+zc,其中不正确的命题为________.【来源:21·世纪·教育·网】
解析 ①a,b共线,包括a与b重合,所以①错.
②空间任意两个向量均共面,所以②错.
③以空间向量的一组基底{a,b,c}为例,知它们两两共面,但它们三个不共面,所以③错.
④当与a,b,c共面时,不成立,所以④错.
答案 ①②③④
三、解答题(本大题共6小题,满分70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量,,是否可以组成一个基底,并说明理由.21·世纪*教育网
解 ,,不可以组成一个基底.理由如下:
连接AC,BD相交于点O,
∵ABCD是平行四边形,
∴O是AC,BD的中点.
在△MBD中,连接MO,
则=(+).
在△PAC中,M是PC的中点,O是AC的中点
∴=,∴=2=+.
∴,,共面,
故,,不可以组成一个基底.
18.(12分)设a1=2i-j+ ( http: / / www.21cnjy.com )k,a2=i+3j-2k,a3=-2i+j-3k,a4=3i+2j+5k,试问是否存在实数a,b,c使a4=aa1+ba2+ca3成立?如果存在,求出a,b,c的值;如果不存在,请说明理由.
解 假设a4=aa1+ba2+ca3成立.
由已知a1=(2,-1,1),a2=(1,3,-2),
a3=(-2,1,-3),a4=(3,2,5),可得
(2a+b-2c,-a+3b+c,a-2b-3c)=(3,2,5).
∴
解得:a=-2,b=1,c=-3.
故有a4=-2a1+a2-3a3.
综上知,满足题意的实数存在,
且a=-2,b=1,c=-3.
19.(12分)四棱柱ABCD-A ( http: / / www.21cnjy.com )′B′C′D′中,AB=5,AD=3,AA′=7,∠BAD=60°,∠BAA′=∠DAA′=45°,求AC′的长.
解 =++=++,
∴()2=(++)2
=2+2+2+2(·+·+·)
=25+9+49+2(5×3cos60°+5×7cos45°+3×7cos45°)
=98+56.
∴||=,
即AC′的长为.
20.(12分)如图所示,PD垂直于正方形ABCD所在的平面,AB=2,PC与平面ABCD所成角是45°,F是AD的中点,M是PC的中点.www-2-1-cnjy-com
求证:DM∥平面PFB.
证明 以D为原点建立如图所示的空间直角坐标系 ( http: / / www.21cnjy.com ),由PC与平面ABCD所成的角为45°,即∠PCD=45°,得PD=2,则P(0,0,2),C(0,2,0),B(2,2,0),F(1,0,0),D(0,0,0),M(0,1,1),【来源:21cnj*y.co*m】
∴=(1,2,0),=(-1,0,2),=(0,1,1).
设平面PFB的法向量为n=(x,y,z),则
∴即
令y=1,则x=-2,z=-1.
故平面PFB的一个法向量为n=(-2,1,-1).
∵·n=0,∴⊥n.
又DM 平面PFB,则DM∥平面PFB.
21.(12分)
如图,正四棱柱ABCD—A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.
(1)证明A1C⊥平面BED;
(2)求二面角A1-DE-B的余弦值.
解 以D为坐标原点,射线DA为x轴的正半轴,建立如图所示的空间直角坐标系D-xyz.
依题设B(2,2,0),C(0,2,0),E(0,2,1),A1(2,0,4).
=(0,2,1),=(2,2,0),
=(-2,2,-4),=(2,0,4).
(1)∵·=0,·=0,
∴A1C⊥BD,A1C⊥DE.
又DB∩DE=D,
∴A1C⊥平面DBE.
(2)设向量n=(x,y,z)是平面DA1E的法向量,则n⊥,n⊥.
∴2y+z=0,2x+4z=0.
令y=1,则z=-2,x=4,
∴n=(4,1,-2).
∴cos〈n,〉==.
∵〈n,〉等于二面角A1-DE-B的平面角,
∴二面角A1-DE-B的余弦值为.
22.(12分)正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点.
(1)证明:平面AED⊥平面A1FD1;
(2)在AE上求一点M,使得A1M⊥平面DAE.
解 (1)证明:建立如图所 ( http: / / www.21cnjy.com )示的空间直角坐标系D-xyz,不妨设正方体的棱长为2,则A(2,0,0),E(2,2,1),F(0,1,0),A1(2,0,2),D1(0,0,2).
设平面AED的法向量为n1=(x1,y1,z1),则
∴
令y1=1,得n1=(0,1,-2).
同理可得平面A1FD1的法向量n2=(0,2,1).
∵n1·n2=0,∴平面AED⊥平面A1FD1.
(2)由于点M在AE上,
∴可设=λ=λ(0,2,1)=(0,2λ,λ),
可得M(2,2λ,λ),于是=(0,2λ,λ-2).
要使A1M⊥平面DAE,需A1M⊥AE,
∴·=(0,2λ,λ-2)·(0,2,1)=5λ-2=0,得λ=.
故当AM=AE时,即点M坐标为(2,,)时,A1M⊥平面DAE.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第三章测试
(时间:120分钟,满分:150分)
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的)
1.向量a=(2x,1,3),b=(1,-2y,9),若a与b共线,则( )
A.x=1,y=1 B.x=,y=-
C.x=,y=- D.x=-,y=
解析 由a∥b知,a=λb,∴2x=λ,1=-2λy,3=9λ,∴λ=,x=,y=-.
答案 C
2.已知a=(-3,2,5),b=(1,x,-1),且a·b=2,则x的值是( )
A.6 B.5
C.4 D.3
解析 a·b=-3+2x-5=2,∴x=5.
答案 B
3.设l1的方向向量为a=(1,2,-2),l2的方向向量为b=(-2,3,m),若l1⊥l2,则实数m的值为( )2-1-c-n-j-y
A.3 B.2
C.1 D.
解析 ∵l1⊥l2,∴a⊥b,∴a·b=0,∴-2+6-2m=0,∴m=2.
答案 B
4.若a,b均为非零向量,则a·b=|a||b|是a与b共线的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
解析 ∵a·b=|a||b|cos〈a,b〉,而a·b=|a||b|.
∴cos〈a,b〉=1,∴〈a,b〉=0.
∴a与b共线.反之,若a与b共线,也可能a·b=-|a|·|b|,因此应选B.
答案 B
5.如图所示,正方体ABCD-A1B1C ( http: / / www.21cnjy.com )1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是( )2·1·c·n·j·y
A.相交 B.平行
C.垂直 D.不能确定
解析 =++=++
=(+)++(+)
=++.
而是平面BB1C1C的一个法向量,且·=·=0,
∴⊥.
又MN 平面BB1C1C,∴MN∥平面BB1C1C.
答案 B
6.已知a,b,c是空间的一个基底,设p=a+b,q=a-b,则下列向量中可以与p,q一起构成空间的另一个基底的是( )
A.a B.b
C.c D.以上都不对
解析 ∵a,b,c不共面,
∴a+b,a-b,c不共面,∴p,q,c可构成空间的一个基底.
答案 C
7.已知△ABC的三个顶点A(3,3,2),B(4,-3,7),C(0,5,1),则BC边上的中线长为( ) 21*cnjy*com
A.2 B.3
C. D.
解析 BC的中点D的坐标为(2,1,4),
∴=(-1,-2,2).
∴||==3.
答案 B
8.与向量a=(2,3,6)共线的单位向量是( )
A.(,,)
B.(-,-,-)
C.(,-,-)和(-,,)
D.(,,)和(-,-,-)
解析 |a|==7,∴与a共线的单位向量是±(2,3,6),故应选D.
答案 D
9.已知向量a=(2,4,x),b=(2,y,2),若|a|=6且a⊥b,则x+y为( )
A.-3或1 B.3或-1
C.-3 D.1
解析 由|a|=6,a⊥b,
得解得或
∴x+y=1,或-3.
答案 A
10.已知a=(x,2,0),b=(3,2-x,x2),且a与b的夹角为钝角,则实数x的取值范围是( )21教育网
A.x>4 B.x<-4
C.0
答案 B
11.已知空间四个点A(1,1,1),B( ( http: / / www.21cnjy.com )-4,0,2),C(-3,-1,0),D(-1,0,4),则直线AD与平面ABC所成的角为( )www.21-cn-jy.com
A.30° B.45°
C.60° D.90°
解析 设平面ABC的一个法向量为n=(x,y,z),
∵=(-5,-1,1),=(-4,-2,-1),
由n·=0及n·=0,得
令z=1,
得x=,y=-,∴n=(,-,1).
又=(-2,-1,3),设AD与平面ABC所成的角为θ,则
sinθ===,
∴θ=30°.
答案 A
12.如图所示,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )
A. B.
C. D.
解析 不妨令CB=1,则CA=CC1=2,得O(0,0,0),B(0,0,1),C1(0,2,0),A(2,0,0),B1(0,2,1),21·cn·jy·com
∴=(0,2,-1),=(-2,2,1).
∴cos〈,〉===.
答案 A
二、填空题(本大题共4小题,每小题5分,满分20分.把答案填在题中横线上)
13.已知{i,j,k}为单位正交基底,且 ( http: / / www.21cnjy.com )a=-i+j+3k,b=2i-3j-2k,则向量a+b与向量a-2b的坐标分别是________;________.
解析 依题意知,a=(-1,1,3),b=(2,-3,-2),则a+b=(1,-2,1),
a-2b=(-1,1,3)-2(2,-3,-2)=(-5,7,7).
答案 (1,-2,1) (-5,7,7)
14.在△ABC中,已知=(2,4,0),=(-1,3,0),则∠ABC=________.
解析 cos〈,〉===,
∴〈,〉=,∴∠ABC=π-=.
答案
15.正方体ABCD-A1B1C1D1中,面ABD1与面B1BD1所夹角的大小为________.
解析
建立空间直角坐标系D-xyz,如图.
设正方体的棱长为1,则A(1,0,0),B(1,1,0),B1(1,1,1),D1(0,0,1).
∴=(1,0,-1),=(1,1,-1),=(1,1,0).
设平面ABD1的法向量为m ( http: / / www.21cnjy.com )=(x1,y1,z1),平面B1BD1的法向量为n=(x2,y2,z2),则由m·=0,m·=0,可得m=(1,0,1),由n·=0,n·=0,得n=(1,-1,0),∴cos〈m,n〉==.∴所求二平面的大小为60°.21世纪教育网版权所有
答案 60°
16.在下列命题中:①若a,b共线,则 ( http: / / www.21cnjy.com )a,b所在的直线平行;②若a,b所在的直线是异面直线,则a,b一定不共面;③若a,b,c三向量两两共面,则a,b,c三向量一定也共面;④已知三向量a,b,c,则空间任意一个向量p总可以唯一表示为p=xa+yb+zc,其中不正确的命题为________.【来源:21·世纪·教育·网】
解析 ①a,b共线,包括a与b重合,所以①错.
②空间任意两个向量均共面,所以②错.
③以空间向量的一组基底{a,b,c}为例,知它们两两共面,但它们三个不共面,所以③错.
④当与a,b,c共面时,不成立,所以④错.
答案 ①②③④
三、解答题(本大题共6小题,满分70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量,,是否可以组成一个基底,并说明理由.21·世纪*教育网
解 ,,不可以组成一个基底.理由如下:
连接AC,BD相交于点O,
∵ABCD是平行四边形,
∴O是AC,BD的中点.
在△MBD中,连接MO,
则=(+).
在△PAC中,M是PC的中点,O是AC的中点
∴=,∴=2=+.
∴,,共面,
故,,不可以组成一个基底.
18.(12分)设a1=2i-j+ ( http: / / www.21cnjy.com )k,a2=i+3j-2k,a3=-2i+j-3k,a4=3i+2j+5k,试问是否存在实数a,b,c使a4=aa1+ba2+ca3成立?如果存在,求出a,b,c的值;如果不存在,请说明理由.
解 假设a4=aa1+ba2+ca3成立.
由已知a1=(2,-1,1),a2=(1,3,-2),
a3=(-2,1,-3),a4=(3,2,5),可得
(2a+b-2c,-a+3b+c,a-2b-3c)=(3,2,5).
∴
解得:a=-2,b=1,c=-3.
故有a4=-2a1+a2-3a3.
综上知,满足题意的实数存在,
且a=-2,b=1,c=-3.
19.(12分)四棱柱ABCD-A ( http: / / www.21cnjy.com )′B′C′D′中,AB=5,AD=3,AA′=7,∠BAD=60°,∠BAA′=∠DAA′=45°,求AC′的长.
解 =++=++,
∴()2=(++)2
=2+2+2+2(·+·+·)
=25+9+49+2(5×3cos60°+5×7cos45°+3×7cos45°)
=98+56.
∴||=,
即AC′的长为.
20.(12分)如图所示,PD垂直于正方形ABCD所在的平面,AB=2,PC与平面ABCD所成角是45°,F是AD的中点,M是PC的中点.www-2-1-cnjy-com
求证:DM∥平面PFB.
证明 以D为原点建立如图所示的空间直角坐标系 ( http: / / www.21cnjy.com ),由PC与平面ABCD所成的角为45°,即∠PCD=45°,得PD=2,则P(0,0,2),C(0,2,0),B(2,2,0),F(1,0,0),D(0,0,0),M(0,1,1),【来源:21cnj*y.co*m】
∴=(1,2,0),=(-1,0,2),=(0,1,1).
设平面PFB的法向量为n=(x,y,z),则
∴即
令y=1,则x=-2,z=-1.
故平面PFB的一个法向量为n=(-2,1,-1).
∵·n=0,∴⊥n.
又DM 平面PFB,则DM∥平面PFB.
21.(12分)
如图,正四棱柱ABCD—A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.
(1)证明A1C⊥平面BED;
(2)求二面角A1-DE-B的余弦值.
解 以D为坐标原点,射线DA为x轴的正半轴,建立如图所示的空间直角坐标系D-xyz.
依题设B(2,2,0),C(0,2,0),E(0,2,1),A1(2,0,4).
=(0,2,1),=(2,2,0),
=(-2,2,-4),=(2,0,4).
(1)∵·=0,·=0,
∴A1C⊥BD,A1C⊥DE.
又DB∩DE=D,
∴A1C⊥平面DBE.
(2)设向量n=(x,y,z)是平面DA1E的法向量,则n⊥,n⊥.
∴2y+z=0,2x+4z=0.
令y=1,则z=-2,x=4,
∴n=(4,1,-2).
∴cos〈n,〉==.
∵〈n,〉等于二面角A1-DE-B的平面角,
∴二面角A1-DE-B的余弦值为.
22.(12分)正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点.
(1)证明:平面AED⊥平面A1FD1;
(2)在AE上求一点M,使得A1M⊥平面DAE.
解 (1)证明:建立如图所 ( http: / / www.21cnjy.com )示的空间直角坐标系D-xyz,不妨设正方体的棱长为2,则A(2,0,0),E(2,2,1),F(0,1,0),A1(2,0,2),D1(0,0,2).
设平面AED的法向量为n1=(x1,y1,z1),则
∴
令y1=1,得n1=(0,1,-2).
同理可得平面A1FD1的法向量n2=(0,2,1).
∵n1·n2=0,∴平面AED⊥平面A1FD1.
(2)由于点M在AE上,
∴可设=λ=λ(0,2,1)=(0,2λ,λ),
可得M(2,2λ,λ),于是=(0,2λ,λ-2).
要使A1M⊥平面DAE,需A1M⊥AE,
∴·=(0,2λ,λ-2)·(0,2,1)=5λ-2=0,得λ=.
故当AM=AE时,即点M坐标为(2,,)时,A1M⊥平面DAE.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
