1.1.2 空间向量的数量积运算 学案(含解析)
文档属性
| 名称 | 1.1.2 空间向量的数量积运算 学案(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 286.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 08:51:17 | ||
图片预览

文档简介
第一章 空间向量与立体几何
1.1.2 空间向量的数量积运算
学案
学习目标
1.了解空间向量的夹角、模的概念及其表示.
2.掌握空间向量的数量积及其运算律.
3.能运用向量的数量积解决立体几何中的垂直、夹角、距离或长度等问题.
知识汇总
1.空间向量的夹角:已知两个非零向量a,b,在空间任取一点O,作,,则叫做向量a,b的夹角,记作.如果,那么向量a,b互相垂直,记作.
2.空间向量的数量积:已知两个非零向量a,b,则叫做a,b的数量积,记作.即. 零向量与任意向量的数量积为0.
由向量的数量积定义,可得;.
3.空间向量数量积的运算律::,;(交换律);(分配律).
习题检测
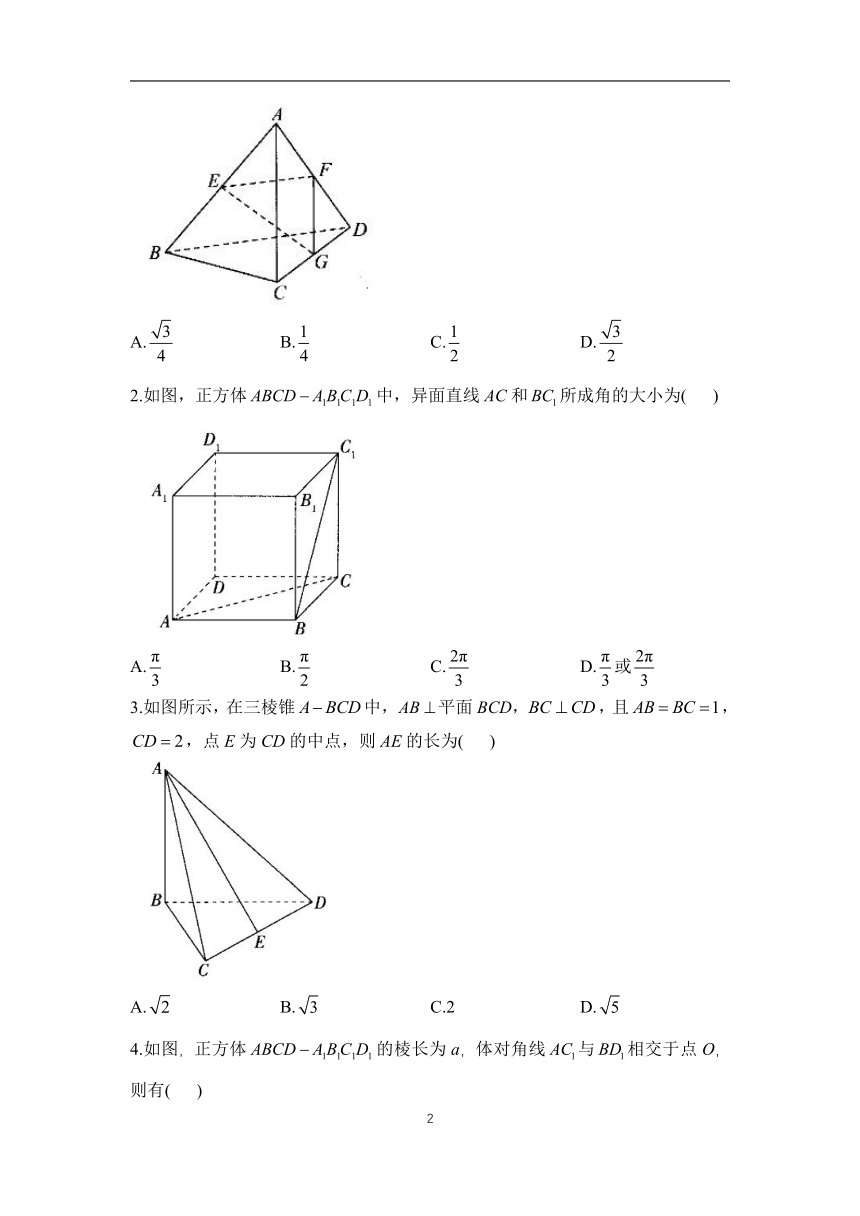
1.如图,空间四边形的每条边和对角线长都等于1,点分别是的中点,则( )
A. B. C. D.
2.如图,正方体中,异面直线AC和所成角的大小为( )
A. B. C. D.或
3.如图所示,在三棱锥中,平面BCD,,且,,点E为CD的中点,则AE的长为( )
A. B. C.2 D.
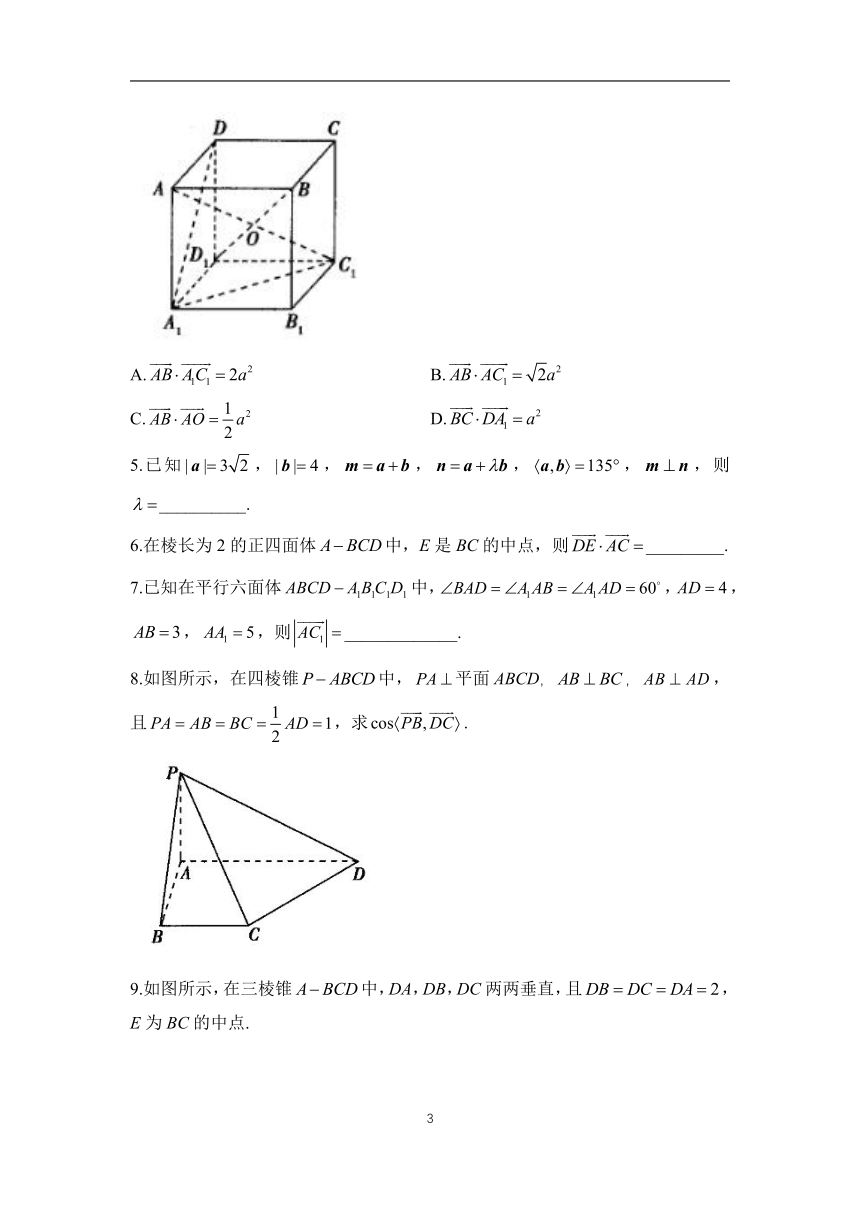
4.如图,正方体的棱长为a,体对角线与相交于点O,则有( )
A. B.
C. D.
5.已知,,,,,,则__________.
6.在棱长为2的正四面体中,E是BC的中点,则_________.
7.已知在平行六面体中,,,,,则_____________.
8.如图所示,在四棱锥中,平面ABCD,,,且,求.
9.如图所示,在三棱锥中,DA,DB,DC两两垂直,且,E为BC的中点.
(1)证明:;
(2)求直线AE与DC所成角的余弦值.
答案以及解析
1.答案:B
解析:由题意得,所以.故选B.
2.答案:A
解析:设正方体的棱长为1,,
,
,
异面直线AC和所成角的大小为.
3.答案:B
解析:
,所以,故选B.
4.答案:C
解析:;
;
;
.故选C.
5.答案:
解析:,,即
,解得.
6.答案:1
解析:
.
7.答案:
解析:六面体是平行六面体,且,
.
又,,,,,
.
8.解析:由题意知,.
因为平面ABCD,
所以,,,
所以.
又,,所以,,
所以,
所以.
9.解析:(1)证明:,,
所以
,
所以.
(2)
,
,
所以,
即直线AE与DC所成角的余弦值为.
2
1.1.2 空间向量的数量积运算
学案
学习目标
1.了解空间向量的夹角、模的概念及其表示.
2.掌握空间向量的数量积及其运算律.
3.能运用向量的数量积解决立体几何中的垂直、夹角、距离或长度等问题.
知识汇总
1.空间向量的夹角:已知两个非零向量a,b,在空间任取一点O,作,,则叫做向量a,b的夹角,记作.如果,那么向量a,b互相垂直,记作.
2.空间向量的数量积:已知两个非零向量a,b,则叫做a,b的数量积,记作.即. 零向量与任意向量的数量积为0.
由向量的数量积定义,可得;.
3.空间向量数量积的运算律::,;(交换律);(分配律).
习题检测
1.如图,空间四边形的每条边和对角线长都等于1,点分别是的中点,则( )
A. B. C. D.
2.如图,正方体中,异面直线AC和所成角的大小为( )
A. B. C. D.或
3.如图所示,在三棱锥中,平面BCD,,且,,点E为CD的中点,则AE的长为( )
A. B. C.2 D.
4.如图,正方体的棱长为a,体对角线与相交于点O,则有( )
A. B.
C. D.
5.已知,,,,,,则__________.
6.在棱长为2的正四面体中,E是BC的中点,则_________.
7.已知在平行六面体中,,,,,则_____________.
8.如图所示,在四棱锥中,平面ABCD,,,且,求.
9.如图所示,在三棱锥中,DA,DB,DC两两垂直,且,E为BC的中点.
(1)证明:;
(2)求直线AE与DC所成角的余弦值.
答案以及解析
1.答案:B
解析:由题意得,所以.故选B.
2.答案:A
解析:设正方体的棱长为1,,
,
,
异面直线AC和所成角的大小为.
3.答案:B
解析:
,所以,故选B.
4.答案:C
解析:;
;
;
.故选C.
5.答案:
解析:,,即
,解得.
6.答案:1
解析:
.
7.答案:
解析:六面体是平行六面体,且,
.
又,,,,,
.
8.解析:由题意知,.
因为平面ABCD,
所以,,,
所以.
又,,所以,,
所以,
所以.
9.解析:(1)证明:,,
所以
,
所以.
(2)
,
,
所以,
即直线AE与DC所成角的余弦值为.
2
