3.2.1 双曲线及其标准方程 学案(含解析)
文档属性
| 名称 | 3.2.1 双曲线及其标准方程 学案(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 274.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 12:27:52 | ||
图片预览



文档简介
第三章 圆锥曲线的方程
3.2.1 双曲线及其标准方程
学案
学习目标
1.经历从具体情境中抽象出双曲线模型的过程.
2.了解双曲线的定义、几何图形和标准方程.
3.通过双曲线标准方程的推导过程理解数形结合思想.
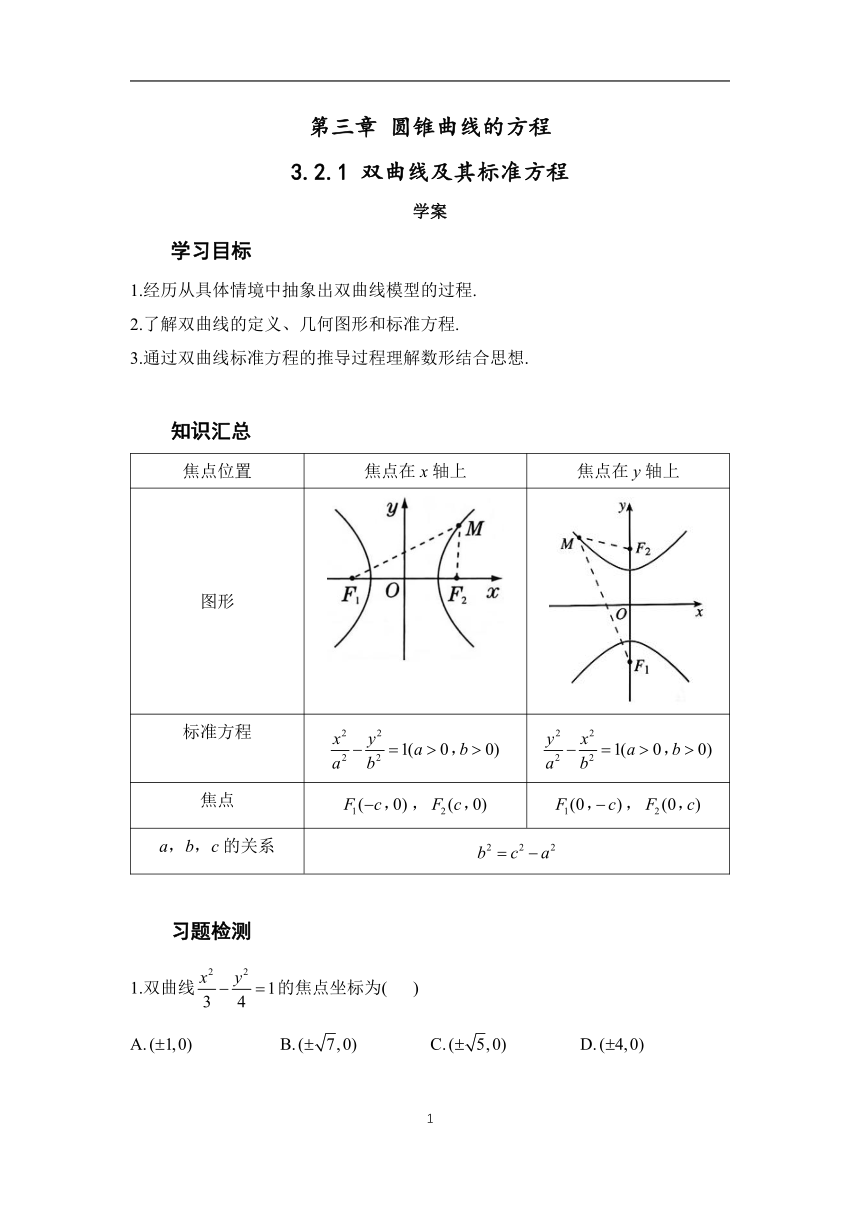
知识汇总
焦点位置 焦点在x轴上 焦点在y轴上
图形
标准方程
焦点 , ,
a,b,c的关系
习题检测
1.双曲线的焦点坐标为( )
A. B. C. D.
2.“”是“方程表示双曲线”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
3.已知双曲线,直线l过其左焦点,交双曲线左支于A,B两点,且为双曲线的右焦点,的周长为20,则m的值为( )
A.8 B.9 C.16 D.20
4.已知双曲线.若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且,,则双曲线E的标准方程是( )
A. B. C. D.
5.(多选)若,是双曲线的左、右焦点,P是双曲线上的一点,且,则下列说法中正确的是( )
A. B.
C.的面积是24 D.的面积是48
6.若双曲线的一个焦点到坐标原点的距离为3,则m的值为____________.
7.过双曲线左焦点的直线交双曲线的左支于M,N两点,为其右焦点,则的值为___________.
8.已知双曲线经过两点,.求该双曲线的标准方程及其焦距.
9.已知双曲线C与椭圆有相同的焦点,且经过点.
(1)求双曲线C的方程;
(2)若,是双曲线C的两个焦点,点P在双曲线C上,且,求的面积.
答案以及解析
1.答案:B
解析:由题意得双曲线的焦点在x轴上,且,,半焦距,双曲线的焦点坐标为.故选B.
2.答案:B
解析:当时,,,方程表示焦点在y轴上的双曲线;但当时,,,方程也表示双曲线,所以“”是“方程表示双曲线”的充分不必要条件.故选B.
3.答案:B
解析:由已知,.又,则.根据双曲线的定义,,所以,即,所以.故选B.
4.答案:D
解析:如图,由题意知.设AB,CD的中点分别为M,N,在中,,所以,,由双曲线的定义可得,即,所以,故双曲线E的标准方程为.故选D.
5.答案:ABC
解析:由题意得,,则.由,得,,故A,B正确;因为,所以是直角三角形,面积,故C正确,D错误.故选ABC.
6.答案:7或-2
解析:依题意可知,当双曲线的焦点在x轴上时,,,所以;当双曲线的焦点在y轴上时,,,所以.综上,或.
7.答案:8
解析:由双曲线的方程可知.因为M,N两点在双曲线的左支上,所以由双曲线定义得,,所以,而,所以.
8.解析:设双曲线方程为.
由题意得,解得,
所以所求双曲线的标准方程为.
因为,,
所以,
故焦距为.
9.解析:(1)椭圆的焦点分别为,,
设双曲线C的方程为,
则.①
又双曲线C经过点,所以.②
由①②得,或,(舍去),
所以双曲线C的方程为.
(2)由双曲线C的方程,知,,.
设,,则,
两边平方得.③
在中,由余弦定理得.④
由③④得.
所以的面积.
2
3.2.1 双曲线及其标准方程
学案
学习目标
1.经历从具体情境中抽象出双曲线模型的过程.
2.了解双曲线的定义、几何图形和标准方程.
3.通过双曲线标准方程的推导过程理解数形结合思想.
知识汇总
焦点位置 焦点在x轴上 焦点在y轴上
图形
标准方程
焦点 , ,
a,b,c的关系
习题检测
1.双曲线的焦点坐标为( )
A. B. C. D.
2.“”是“方程表示双曲线”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
3.已知双曲线,直线l过其左焦点,交双曲线左支于A,B两点,且为双曲线的右焦点,的周长为20,则m的值为( )
A.8 B.9 C.16 D.20
4.已知双曲线.若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且,,则双曲线E的标准方程是( )
A. B. C. D.
5.(多选)若,是双曲线的左、右焦点,P是双曲线上的一点,且,则下列说法中正确的是( )
A. B.
C.的面积是24 D.的面积是48
6.若双曲线的一个焦点到坐标原点的距离为3,则m的值为____________.
7.过双曲线左焦点的直线交双曲线的左支于M,N两点,为其右焦点,则的值为___________.
8.已知双曲线经过两点,.求该双曲线的标准方程及其焦距.
9.已知双曲线C与椭圆有相同的焦点,且经过点.
(1)求双曲线C的方程;
(2)若,是双曲线C的两个焦点,点P在双曲线C上,且,求的面积.
答案以及解析
1.答案:B
解析:由题意得双曲线的焦点在x轴上,且,,半焦距,双曲线的焦点坐标为.故选B.
2.答案:B
解析:当时,,,方程表示焦点在y轴上的双曲线;但当时,,,方程也表示双曲线,所以“”是“方程表示双曲线”的充分不必要条件.故选B.
3.答案:B
解析:由已知,.又,则.根据双曲线的定义,,所以,即,所以.故选B.
4.答案:D
解析:如图,由题意知.设AB,CD的中点分别为M,N,在中,,所以,,由双曲线的定义可得,即,所以,故双曲线E的标准方程为.故选D.
5.答案:ABC
解析:由题意得,,则.由,得,,故A,B正确;因为,所以是直角三角形,面积,故C正确,D错误.故选ABC.
6.答案:7或-2
解析:依题意可知,当双曲线的焦点在x轴上时,,,所以;当双曲线的焦点在y轴上时,,,所以.综上,或.
7.答案:8
解析:由双曲线的方程可知.因为M,N两点在双曲线的左支上,所以由双曲线定义得,,所以,而,所以.
8.解析:设双曲线方程为.
由题意得,解得,
所以所求双曲线的标准方程为.
因为,,
所以,
故焦距为.
9.解析:(1)椭圆的焦点分别为,,
设双曲线C的方程为,
则.①
又双曲线C经过点,所以.②
由①②得,或,(舍去),
所以双曲线C的方程为.
(2)由双曲线C的方程,知,,.
设,,则,
两边平方得.③
在中,由余弦定理得.④
由③④得.
所以的面积.
2
