3.3.2 抛物线的简单几何性质 学案(含解析)
文档属性
| 名称 | 3.3.2 抛物线的简单几何性质 学案(含解析) | 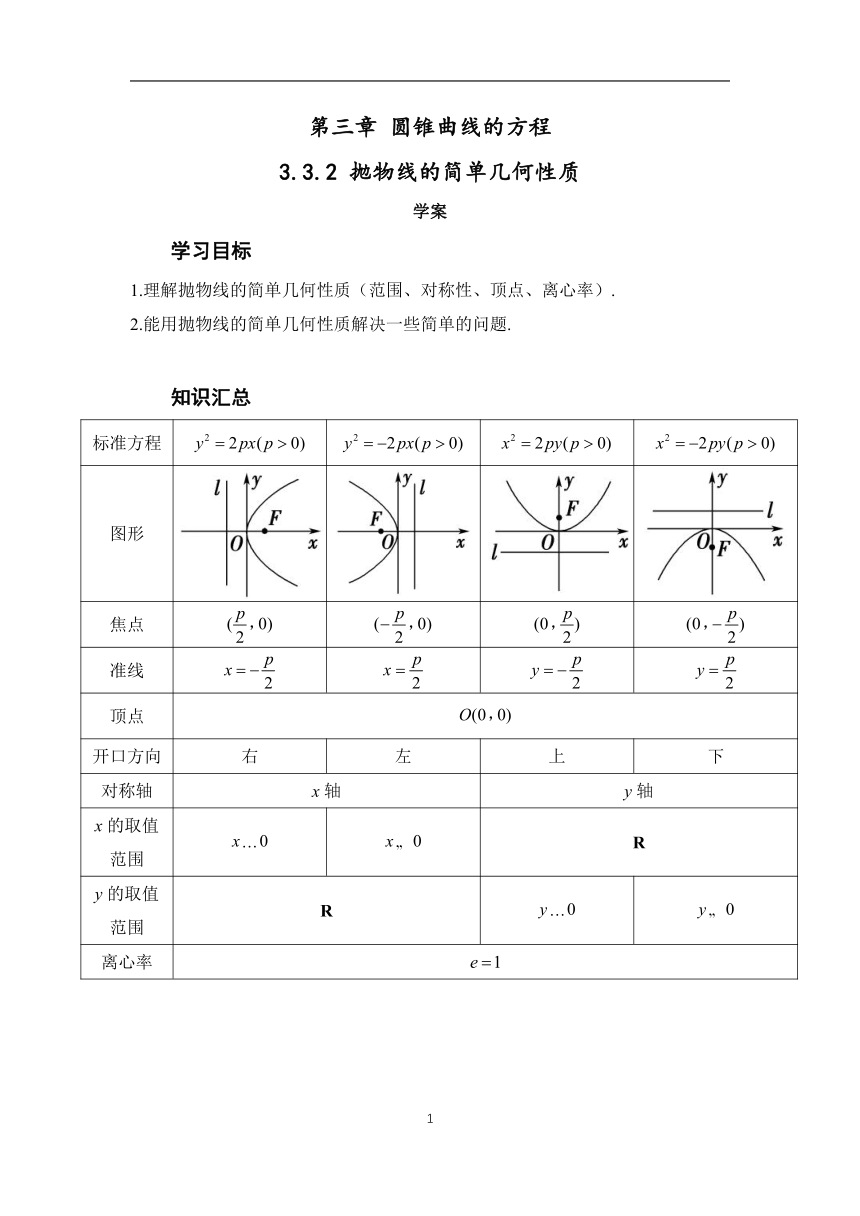 | |
| 格式 | docx | ||
| 文件大小 | 342.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 12:29:07 | ||
图片预览



文档简介
第三章 圆锥曲线的方程
3.3.2 抛物线的简单几何性质
学案
学习目标
1.理解抛物线的简单几何性质(范围、对称性、顶点、离心率).
2.能用抛物线的简单几何性质解决一些简单的问题.
知识汇总
标准方程
图形
焦点
准线
顶点
开口方向 右 左 上 下
对称轴 x轴 y轴
x的取值范围 R
y的取值范围 R
离心率
习题检测
1.已知A为拋物线上的一点,点A到抛物线C的焦点的距离为12,到y轴的距离为9,则p的值为( )
A.2 B.3 C.6 D.9
2.已知抛物线和直线,在抛物线上有一动点P到y轴的距离为,到直线l的距离为,则的最小值为( )
A. B. C. D.
3.过抛物线的焦点F作倾斜角为60°的直线交拋物线于A,B两点,若线段AB的长为8,则p的值为( )
A.-3 B.1 C.3 D.4
4.已知抛物线M的顶点在原点,焦点在y轴正半轴上,过其焦点F作直线l交抛物线于A,B两点,过点A,B分别作抛物线准线的垂线,垂足分别为点C,D,,且,则该抛物线的方程为( )
A. B. C. D.
5.过抛物线焦点F的直线交抛物线于两点,交其准线于点C,且位于x轴同侧.若,则( )
A.2 B.3 C.4 D.5
6.(多选)已知抛物线的焦点为F,准线为l,过F的直线与E交于A,B两点,C,D分别为A,B在l上的射影,且,M为AB中点,则下列结论正确的是( )
A.
B.为等腰直角三角形
C.直线AB的斜率为
D.的面积为4
7.若抛物线上一点到抛物线准线的距离为,则抛物线的方程为______________.
8.已知抛物线,点P为抛物线上任意一点,过点P向圆作切线,切点分别为A,B,则四边形PADB的面积的最小值为_______.
9.已知抛物线的焦点为F,点在抛物线C上,且.
(1)求抛物线C的方程;
(2)过焦点F的直线l与抛物线分别交于A,B两点,点A,B的坐标分别为,,O为坐标原点,若,求直线l的方程.
答案以及解析
1.答案:C
解析:由拋物线定义知点A到拋物线C的焦点的距离等于到准线的距离,则,解得.故选C.
2.答案:D
解析:设抛物线的焦点为F,过P作PA与抛物线的准线垂直,垂足为A,作PB与l垂直,垂足为B,则,显然当P,F,B三点共线(即点P在线段BF上)时,取得最小值,最小值为.故选D.
3.答案:C
解析:由题意可知过焦点且倾斜角为60°的直线方程为,与抛物线方程联立得,消去y并整理,得,设点,,则,所以,解得.故选C.
4.答案:A
解析:设,,,抛物线的方程为,因为,所以,,所以,,,,因为,所以,所以,所以抛物线的方程为.故选A.
5.答案:C
解析:设抛物线的准线为l,准线l与x轴交于点H,则,,,过A作,垂足为D,由抛物线的定义可知,,,,则,
,,,故选C.
6.答案:AC
解析:由,得,即,焦点,准线.
设直线AB的方程为,,,由,得,,,从而,,又,,即,因此,且或(舍去),,,即直线AB的斜率为,故C正确;选项A中,,,,从而,故A正确;
选项B中,,,结合图形知不是直角三角形,故B错误;
选项D中,,故D错误.故选AC.
7.答案:
解析:因为点A在抛物线上,所以,,点A到抛物线准线的距离为,解得或,当时,,不符合题意,舍去,所以,故抛物线的方程为.
8.答案:
解析:如图,连接PD,圆,该圆的圆心与抛物线的焦点重合,半径为1,则.又,所以当四边形PADB的面积最小时,最小.过点P向抛物线的准线作垂线,垂足为E,则,当点P与坐标原点重合时,最小,此时.故.
9.解析:(1)由点在抛物线C上,
得,解得,
由抛物线定义得,,解得,
故抛物线C的方程为.
(2)设直线l的方程为,
联立消去x,得,
故,,
所以,,
则,即,解得,
所以所求直线l的方程为或.
2
3.3.2 抛物线的简单几何性质
学案
学习目标
1.理解抛物线的简单几何性质(范围、对称性、顶点、离心率).
2.能用抛物线的简单几何性质解决一些简单的问题.
知识汇总
标准方程
图形
焦点
准线
顶点
开口方向 右 左 上 下
对称轴 x轴 y轴
x的取值范围 R
y的取值范围 R
离心率
习题检测
1.已知A为拋物线上的一点,点A到抛物线C的焦点的距离为12,到y轴的距离为9,则p的值为( )
A.2 B.3 C.6 D.9
2.已知抛物线和直线,在抛物线上有一动点P到y轴的距离为,到直线l的距离为,则的最小值为( )
A. B. C. D.
3.过抛物线的焦点F作倾斜角为60°的直线交拋物线于A,B两点,若线段AB的长为8,则p的值为( )
A.-3 B.1 C.3 D.4
4.已知抛物线M的顶点在原点,焦点在y轴正半轴上,过其焦点F作直线l交抛物线于A,B两点,过点A,B分别作抛物线准线的垂线,垂足分别为点C,D,,且,则该抛物线的方程为( )
A. B. C. D.
5.过抛物线焦点F的直线交抛物线于两点,交其准线于点C,且位于x轴同侧.若,则( )
A.2 B.3 C.4 D.5
6.(多选)已知抛物线的焦点为F,准线为l,过F的直线与E交于A,B两点,C,D分别为A,B在l上的射影,且,M为AB中点,则下列结论正确的是( )
A.
B.为等腰直角三角形
C.直线AB的斜率为
D.的面积为4
7.若抛物线上一点到抛物线准线的距离为,则抛物线的方程为______________.
8.已知抛物线,点P为抛物线上任意一点,过点P向圆作切线,切点分别为A,B,则四边形PADB的面积的最小值为_______.
9.已知抛物线的焦点为F,点在抛物线C上,且.
(1)求抛物线C的方程;
(2)过焦点F的直线l与抛物线分别交于A,B两点,点A,B的坐标分别为,,O为坐标原点,若,求直线l的方程.
答案以及解析
1.答案:C
解析:由拋物线定义知点A到拋物线C的焦点的距离等于到准线的距离,则,解得.故选C.
2.答案:D
解析:设抛物线的焦点为F,过P作PA与抛物线的准线垂直,垂足为A,作PB与l垂直,垂足为B,则,显然当P,F,B三点共线(即点P在线段BF上)时,取得最小值,最小值为.故选D.
3.答案:C
解析:由题意可知过焦点且倾斜角为60°的直线方程为,与抛物线方程联立得,消去y并整理,得,设点,,则,所以,解得.故选C.
4.答案:A
解析:设,,,抛物线的方程为,因为,所以,,所以,,,,因为,所以,所以,所以抛物线的方程为.故选A.
5.答案:C
解析:设抛物线的准线为l,准线l与x轴交于点H,则,,,过A作,垂足为D,由抛物线的定义可知,,,,则,
,,,故选C.
6.答案:AC
解析:由,得,即,焦点,准线.
设直线AB的方程为,,,由,得,,,从而,,又,,即,因此,且或(舍去),,,即直线AB的斜率为,故C正确;选项A中,,,,从而,故A正确;
选项B中,,,结合图形知不是直角三角形,故B错误;
选项D中,,故D错误.故选AC.
7.答案:
解析:因为点A在抛物线上,所以,,点A到抛物线准线的距离为,解得或,当时,,不符合题意,舍去,所以,故抛物线的方程为.
8.答案:
解析:如图,连接PD,圆,该圆的圆心与抛物线的焦点重合,半径为1,则.又,所以当四边形PADB的面积最小时,最小.过点P向抛物线的准线作垂线,垂足为E,则,当点P与坐标原点重合时,最小,此时.故.
9.解析:(1)由点在抛物线C上,
得,解得,
由抛物线定义得,,解得,
故抛物线C的方程为.
(2)设直线l的方程为,
联立消去x,得,
故,,
所以,,
则,即,解得,
所以所求直线l的方程为或.
2
