22.1.2二次函数y=ax2的图象和性质(教案)初中数学人教版九年级上册
文档属性
| 名称 | 22.1.2二次函数y=ax2的图象和性质(教案)初中数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 953.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 11:44:54 | ||
图片预览


文档简介
第二十二章 二次函数
22.1.2二次函数y=ax2的图象和性质
教学设计
一、教学目标
1.会用描点法画出形如的二次函数图象,连接抛物线的有关概念
2.能通过观察图象说出二次函数的图象特征和性质
3.会用待定系数法确定二次函数的解析式
4.在类比探究二次函数的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想
二、教学重难点
1. 教学重点
二次函数的图象的画法及性质
2. 教学难点
用描点法画二次函数的图象,探索其性质及特征
三、教学过程
(一)新课导入
让学生观看生活中的抛物线
我们研究问题最好是由最简的情形入手,而根据二次函数的定义,你认为最简单的二次函数的解析式是怎样的?
学生独立思考,得出答案:最简单的二次函数是,我们这节课就学习二次函数的图象和性质.
(二)探索新知
探究一:画出二次函数的图象
自变量x的取值范围是什么?x取整数还是取其他数较好?y是一个数的平方,它的值与x的值有什么关系?
学生可能有多种答法,引导学生回答:当x取互为相反数的两个数时,y的值相同.
1.列表:在中自变量x可以是任意实数,列表表示几组对应值:
2.描点:根据表中x,y的数值在坐标平面中描点(x,y)
(教师提问:在画坐标系时,x轴的正、负半轴和y轴的正、负半轴是否都要画的一样长?学生独立思考,小组讨论,得出共识如下:x轴的正、负半轴画一样的长,y的正半轴画的较长,负半轴画的较短就可以.通过这个问题可以培养学生的作图技巧.)
3.连线:如图,再用平滑曲线顺次连接各点,就得到的图象.
(学生先连一次试试,教师再演示.)
根据图象可以看出:y轴是抛物线的对称轴,抛物线与它的对称轴的交点叫做抛物线的顶点,它是抛物线的最低点.
(教师可根据学生理解的层次直接根据解析式得出图象是轴对称图形)
议一议
根据你以往学习函数图象性质的经验,说说二次函数y=x2的图象有哪些性质,并与同伴交流.
(1)y=x2是一条抛物线;
(2)图象开口向上;
(3)图象关于y轴对称;
(4)顶点
(5)图象有最低点
提问:观察二次函数y=x2的图象,y随x如何变化
从二次函数y=x2的图象可以看出:当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
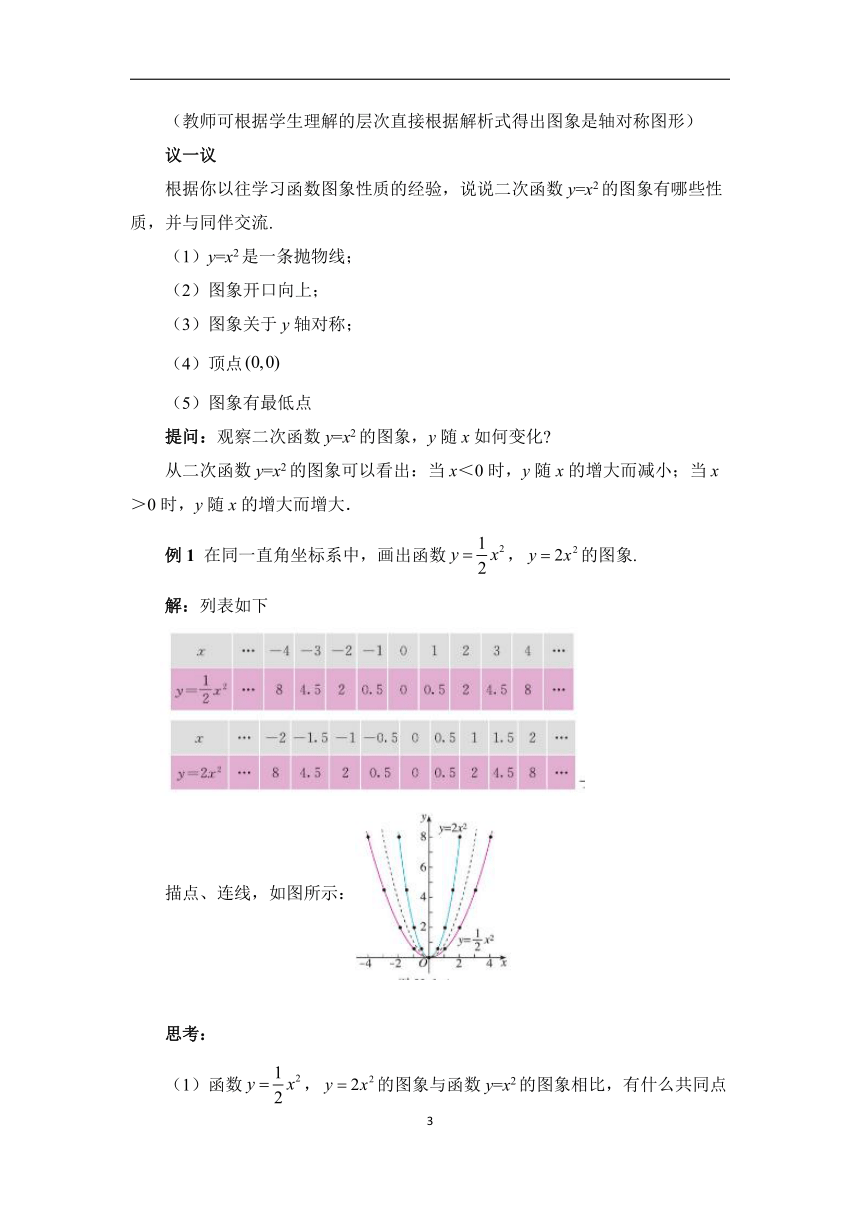
例1 在同一直角坐标系中,画出函数,的图象.
解:列表如下
描点、连线,如图所示:
思考:
(1)函数,的图象与函数y=x2的图象相比,有什么共同点和不同点?
(2)当时,二次函数的图象有什么特点?
答:一般地,当时,抛物线的开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点,a越大,抛物线的开口越小.
探究二
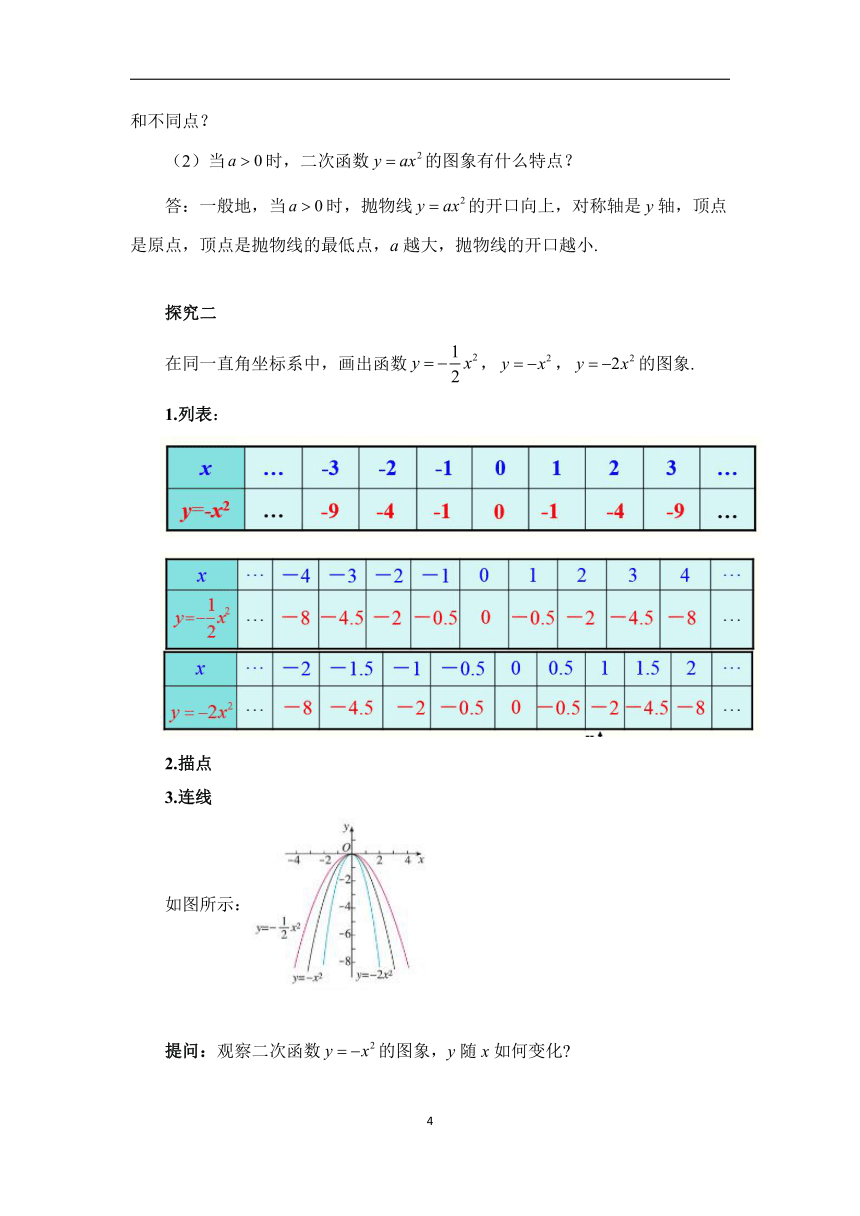
在同一直角坐标系中,画出函数,,的图象.
1.列表:
2.描点
3.连线
如图所示:
提问:观察二次函数的图象,y随x如何变化
从二次函数的图象可以看出:当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
思考:
(1)从函数,,的图象,考虑这些抛物线有什么相同点和不同点.
(2)当a<0时,二次函数y = ax2的图象有什么特点?
答:对于抛物线,抛物线开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点,a越小,抛物线的开口越小.
归纳:
练习
1.已知函数的图像过点.
(1)求a的值;
(2)在图像上有两点,,且,比较,的大小.
解析:(1)因为函数的图像过点,
所以.
(2)由(1)知,.因为,所以图像开口向上,对称轴为y轴,在对称轴左侧,y随x的增大而减小,在对称轴右侧,y随x的增大而增大,所以当时,.
2.已知二次函数与一次函数的图象相交于两点,如图所示,其中,求的面积.(解答可参照图中辅助线)
解析:∵一次函数的图象过点,解得,
∴一次函数解析式为,∴令,得.过点,,解得,∴二次函数解析式为.由一次函数与二次
函数联立可得解得,.
3.如图,在平面直角坐标系中,点A的坐标为,过点A作y轴的平行线交二次数的图象于点B.
(1)点B的纵坐标为____________(用含m的代数式表示);
(2)当点A落在二次函数的图象上时,求m的值;
(3)当时,若,求m的值.
答案:(1)如图,根据题意知,点B的横坐标是m,
将代入,得,
点B的纵坐标为.
(2)把代入,得.
解得,.
(3)根据题意知.
①,解得,.
,.
②,
解得,.
,.
综上所述,m的值为或.
(三)小结作业
小结:
1.本节课我们主要学习了哪些内容?
2.二次函数的画法
3.二次函数的图象
4.二次函数的性质
作业:
四、板书设计
22.1.2二次函数的图象和性质
二次函数的图象;
二次函数的图象
二次函数的图象和性质
2
22.1.2二次函数y=ax2的图象和性质
教学设计
一、教学目标
1.会用描点法画出形如的二次函数图象,连接抛物线的有关概念
2.能通过观察图象说出二次函数的图象特征和性质
3.会用待定系数法确定二次函数的解析式
4.在类比探究二次函数的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想
二、教学重难点
1. 教学重点
二次函数的图象的画法及性质
2. 教学难点
用描点法画二次函数的图象,探索其性质及特征
三、教学过程
(一)新课导入
让学生观看生活中的抛物线
我们研究问题最好是由最简的情形入手,而根据二次函数的定义,你认为最简单的二次函数的解析式是怎样的?
学生独立思考,得出答案:最简单的二次函数是,我们这节课就学习二次函数的图象和性质.
(二)探索新知
探究一:画出二次函数的图象
自变量x的取值范围是什么?x取整数还是取其他数较好?y是一个数的平方,它的值与x的值有什么关系?
学生可能有多种答法,引导学生回答:当x取互为相反数的两个数时,y的值相同.
1.列表:在中自变量x可以是任意实数,列表表示几组对应值:
2.描点:根据表中x,y的数值在坐标平面中描点(x,y)
(教师提问:在画坐标系时,x轴的正、负半轴和y轴的正、负半轴是否都要画的一样长?学生独立思考,小组讨论,得出共识如下:x轴的正、负半轴画一样的长,y的正半轴画的较长,负半轴画的较短就可以.通过这个问题可以培养学生的作图技巧.)
3.连线:如图,再用平滑曲线顺次连接各点,就得到的图象.
(学生先连一次试试,教师再演示.)
根据图象可以看出:y轴是抛物线的对称轴,抛物线与它的对称轴的交点叫做抛物线的顶点,它是抛物线的最低点.
(教师可根据学生理解的层次直接根据解析式得出图象是轴对称图形)
议一议
根据你以往学习函数图象性质的经验,说说二次函数y=x2的图象有哪些性质,并与同伴交流.
(1)y=x2是一条抛物线;
(2)图象开口向上;
(3)图象关于y轴对称;
(4)顶点
(5)图象有最低点
提问:观察二次函数y=x2的图象,y随x如何变化
从二次函数y=x2的图象可以看出:当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
例1 在同一直角坐标系中,画出函数,的图象.
解:列表如下
描点、连线,如图所示:
思考:
(1)函数,的图象与函数y=x2的图象相比,有什么共同点和不同点?
(2)当时,二次函数的图象有什么特点?
答:一般地,当时,抛物线的开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点,a越大,抛物线的开口越小.
探究二
在同一直角坐标系中,画出函数,,的图象.
1.列表:
2.描点
3.连线
如图所示:
提问:观察二次函数的图象,y随x如何变化
从二次函数的图象可以看出:当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
思考:
(1)从函数,,的图象,考虑这些抛物线有什么相同点和不同点.
(2)当a<0时,二次函数y = ax2的图象有什么特点?
答:对于抛物线,抛物线开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点,a越小,抛物线的开口越小.
归纳:
练习
1.已知函数的图像过点.
(1)求a的值;
(2)在图像上有两点,,且,比较,的大小.
解析:(1)因为函数的图像过点,
所以.
(2)由(1)知,.因为,所以图像开口向上,对称轴为y轴,在对称轴左侧,y随x的增大而减小,在对称轴右侧,y随x的增大而增大,所以当时,.
2.已知二次函数与一次函数的图象相交于两点,如图所示,其中,求的面积.(解答可参照图中辅助线)
解析:∵一次函数的图象过点,解得,
∴一次函数解析式为,∴令,得.过点,,解得,∴二次函数解析式为.由一次函数与二次
函数联立可得解得,.
3.如图,在平面直角坐标系中,点A的坐标为,过点A作y轴的平行线交二次数的图象于点B.
(1)点B的纵坐标为____________(用含m的代数式表示);
(2)当点A落在二次函数的图象上时,求m的值;
(3)当时,若,求m的值.
答案:(1)如图,根据题意知,点B的横坐标是m,
将代入,得,
点B的纵坐标为.
(2)把代入,得.
解得,.
(3)根据题意知.
①,解得,.
,.
②,
解得,.
,.
综上所述,m的值为或.
(三)小结作业
小结:
1.本节课我们主要学习了哪些内容?
2.二次函数的画法
3.二次函数的图象
4.二次函数的性质
作业:
四、板书设计
22.1.2二次函数的图象和性质
二次函数的图象;
二次函数的图象
二次函数的图象和性质
2
同课章节目录
