22.1.3.3二次函数y=a(x-h)2+k的图象和性质(教案)初中数学人教版九年级上册
文档属性
| 名称 | 22.1.3.3二次函数y=a(x-h)2+k的图象和性质(教案)初中数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 288.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 00:00:00 | ||
图片预览


文档简介
第二十二章 二次函数
22.1.3.3二次函数的图象和性质
教学设计
一、教学目标
1.能画出二次函数的图象.
2.掌握二次函数与图象之间的联系
3.能灵活运用二次函数的知识解决简单的问题
二、教学重难点
1. 教学重点
二次函数的图象和性质
二次函数与图象之间的联系
2. 教学难点
二次函数性质的应用
三、教学过程
(一)新课导入
二次函数图象可以相互平移得到.
通过左右平移得到
通过上下平移得到
同学们猜想怎样平移能得到
(二)探索新知
探究一
在坐标系中,画出二次函数的图象,并分别指出它的开口方向,对称轴和顶点坐标.
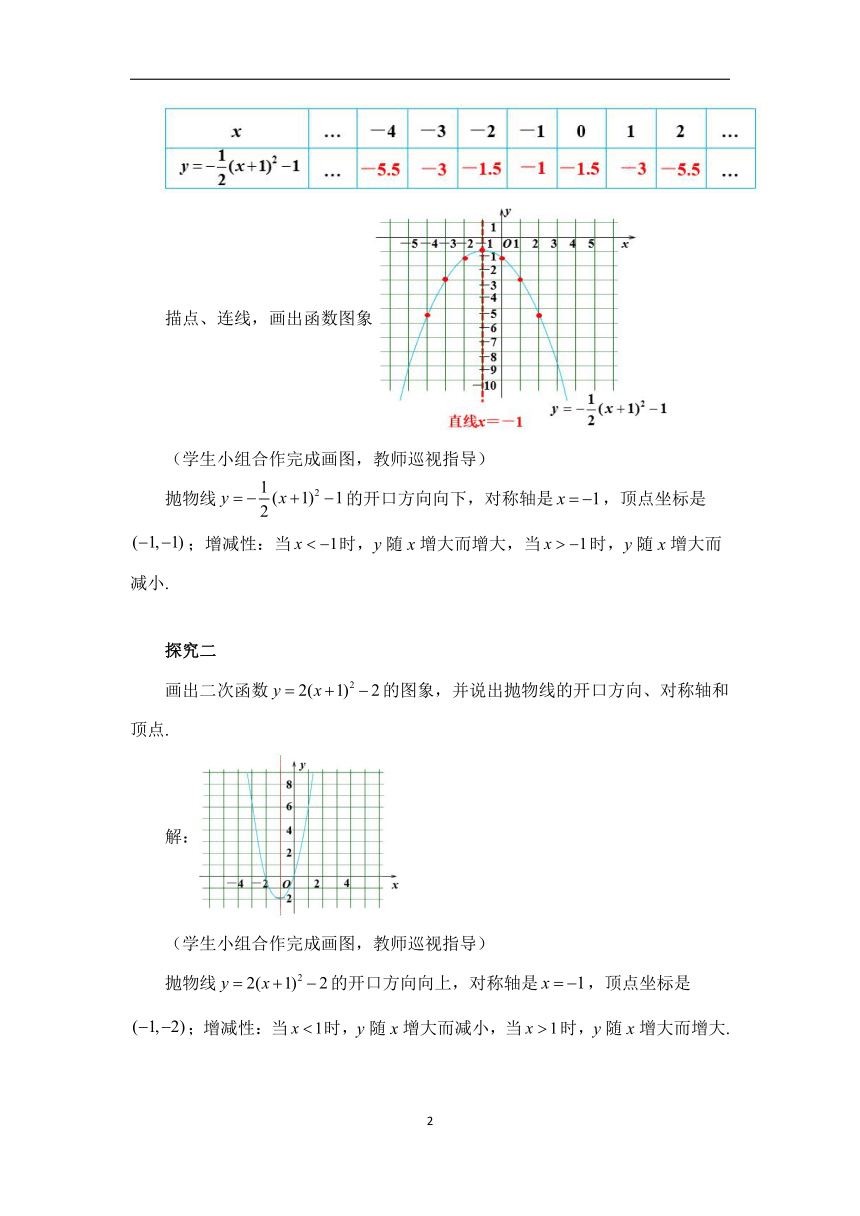
解:列表
描点、连线,画出函数图象
(学生小组合作完成画图,教师巡视指导)
抛物线的开口方向向下,对称轴是,顶点坐标是;增减性:当时,y随x增大而增大,当时,y随x增大而减小.
探究二
画出二次函数的图象,并说出抛物线的开口方向、对称轴和顶点.
解:
(学生小组合作完成画图,教师巡视指导)
抛物线的开口方向向上,对称轴是,顶点坐标是;增减性:当时,y随x增大而减小,当时,y随x增大而增大.
通过上面的两个探究,得到二次函数的性质
教师课件展示空表示,指导学生填写
例1 已知抛物线经过点.
(1)指出抛物线的对称轴;
(2)求a的值;
(3)若点,都在该抛物线上,试比较与的大小.
解:(1)由可知其顶点为,对称轴为直线.
(2)因为抛物线经过点,
所以,解得.
(3),
此函数的图象开口向下,当时,y随x的增大而增大.
点,都在该抛物线上,
.
思考
怎样移动抛物线就可以得到抛物线?
方法一:向下平移1个单位长度得到,
向左平移1个单位长度得到.
方法二:向左平移1个单位长度得到,
向下平移1个单位长度得到.
归纳总结
一般地,抛物线与形状相同,位置不同.把抛物线向上(下)向左(右)平移,可以得到抛物线.
对于二次函数图象性质中,字母a,h,k所起的作用不同:① a决定开口方向;② 决定顶点坐标.h决定对称轴(直线).,对称轴在y轴的左侧;,对称轴在y轴的右侧;,顶点在x轴的上侧;,顶点在x轴的下侧.③ a,h(对称轴)决定函数的增减性.
例2 要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1 m处达到最高,高度为3 m,水柱落地处离池中心3 m,水管应多长?
解:如图,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立直角坐标系.
点是图中这段抛物线的顶点,
因此,可设这段抛物线对应的函数是.
由着段抛物线经过点可得,
解得.
因此.
当时,,也就是说,水管应长2.25m.
练习
1.对于二次函数的图象,下列说法正确的是( )
A.图象与y轴交点的坐标是 B.对称轴是直线
C.顶点坐标为 D.当时,y随x的增大而增大
答案:D
解析:对于二次函数的图象,
A.当时,,图像与y轴交点坐标为,A选项说法不正确;
B.抛物线对称轴为直线,B选项说法不正确;
C.抛物线顶点坐标为,C选项说法不正确;
D.,图像开口向下,
当时,y随x的增大而增大,D选项说法正确;故选D.
2.将函数的图象先向左平移2个单位,再向下平移5个单位,则最终所得图象对应的函数解析式为_________.
答案:
解析:函数的图象先向左平移2个单位,再向下平移5个单位,则最终所得图象对应的函数解析式为,即.故答案为.
3.已知二次函数.
(1)二次函数图象的对称轴为直线_________(用含m的代数式表示)
(2)当时,函数有最大值为4,求实数m的值.
解析:(1)∵二次函数,
∴对称轴为直线,故答案为m.
(2)该抛物线的对称轴为直线.抛物线开口向下,∴当时,y随着x的增大而增大;当时,y随着x的增大而减小.①当时,,∴当时,y取得最大值,即,解得.②当时, 时,y取得最大值,即,解得或(不合题意,舍去).③当时,时,y取得最大值,即,解得(不合题意,舍去).综上,m的值为2或.
(三)小结作业
小结:
1.本节课我们主要学习了哪些内容?
2.二次函数的图象
3.二次函数的性质
4.与的关系
作业:
四、板书设计
22.1.3.3二次函数的图象和性质
探究一:二次函数的图象
探究二:二次函数的图象
二次函数的性质总结
例题
2
22.1.3.3二次函数的图象和性质
教学设计
一、教学目标
1.能画出二次函数的图象.
2.掌握二次函数与图象之间的联系
3.能灵活运用二次函数的知识解决简单的问题
二、教学重难点
1. 教学重点
二次函数的图象和性质
二次函数与图象之间的联系
2. 教学难点
二次函数性质的应用
三、教学过程
(一)新课导入
二次函数图象可以相互平移得到.
通过左右平移得到
通过上下平移得到
同学们猜想怎样平移能得到
(二)探索新知
探究一
在坐标系中,画出二次函数的图象,并分别指出它的开口方向,对称轴和顶点坐标.
解:列表
描点、连线,画出函数图象
(学生小组合作完成画图,教师巡视指导)
抛物线的开口方向向下,对称轴是,顶点坐标是;增减性:当时,y随x增大而增大,当时,y随x增大而减小.
探究二
画出二次函数的图象,并说出抛物线的开口方向、对称轴和顶点.
解:
(学生小组合作完成画图,教师巡视指导)
抛物线的开口方向向上,对称轴是,顶点坐标是;增减性:当时,y随x增大而减小,当时,y随x增大而增大.
通过上面的两个探究,得到二次函数的性质
教师课件展示空表示,指导学生填写
例1 已知抛物线经过点.
(1)指出抛物线的对称轴;
(2)求a的值;
(3)若点,都在该抛物线上,试比较与的大小.
解:(1)由可知其顶点为,对称轴为直线.
(2)因为抛物线经过点,
所以,解得.
(3),
此函数的图象开口向下,当时,y随x的增大而增大.
点,都在该抛物线上,
.
思考
怎样移动抛物线就可以得到抛物线?
方法一:向下平移1个单位长度得到,
向左平移1个单位长度得到.
方法二:向左平移1个单位长度得到,
向下平移1个单位长度得到.
归纳总结
一般地,抛物线与形状相同,位置不同.把抛物线向上(下)向左(右)平移,可以得到抛物线.
对于二次函数图象性质中,字母a,h,k所起的作用不同:① a决定开口方向;② 决定顶点坐标.h决定对称轴(直线).,对称轴在y轴的左侧;,对称轴在y轴的右侧;,顶点在x轴的上侧;,顶点在x轴的下侧.③ a,h(对称轴)决定函数的增减性.
例2 要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1 m处达到最高,高度为3 m,水柱落地处离池中心3 m,水管应多长?
解:如图,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立直角坐标系.
点是图中这段抛物线的顶点,
因此,可设这段抛物线对应的函数是.
由着段抛物线经过点可得,
解得.
因此.
当时,,也就是说,水管应长2.25m.
练习
1.对于二次函数的图象,下列说法正确的是( )
A.图象与y轴交点的坐标是 B.对称轴是直线
C.顶点坐标为 D.当时,y随x的增大而增大
答案:D
解析:对于二次函数的图象,
A.当时,,图像与y轴交点坐标为,A选项说法不正确;
B.抛物线对称轴为直线,B选项说法不正确;
C.抛物线顶点坐标为,C选项说法不正确;
D.,图像开口向下,
当时,y随x的增大而增大,D选项说法正确;故选D.
2.将函数的图象先向左平移2个单位,再向下平移5个单位,则最终所得图象对应的函数解析式为_________.
答案:
解析:函数的图象先向左平移2个单位,再向下平移5个单位,则最终所得图象对应的函数解析式为,即.故答案为.
3.已知二次函数.
(1)二次函数图象的对称轴为直线_________(用含m的代数式表示)
(2)当时,函数有最大值为4,求实数m的值.
解析:(1)∵二次函数,
∴对称轴为直线,故答案为m.
(2)该抛物线的对称轴为直线.抛物线开口向下,∴当时,y随着x的增大而增大;当时,y随着x的增大而减小.①当时,,∴当时,y取得最大值,即,解得.②当时, 时,y取得最大值,即,解得或(不合题意,舍去).③当时,时,y取得最大值,即,解得(不合题意,舍去).综上,m的值为2或.
(三)小结作业
小结:
1.本节课我们主要学习了哪些内容?
2.二次函数的图象
3.二次函数的性质
4.与的关系
作业:
四、板书设计
22.1.3.3二次函数的图象和性质
探究一:二次函数的图象
探究二:二次函数的图象
二次函数的性质总结
例题
2
同课章节目录
