22.2二次函数与一元二次方程(教案)初中数学人教版九年级上册
文档属性
| 名称 | 22.2二次函数与一元二次方程(教案)初中数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 281.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 00:00:00 | ||
图片预览


文档简介
第二十二章 二次函数
22.2二次函数与一元二次方程
教学设计
一、教学目标
1.了解一元二次方程的根的几何意义,知道抛物线与x轴的三种位置关系对应着一元二次方程的根的三种情况,会利用二次函数的图象求一元二次方程的近似解.
2.通过探索二次函数与一元二次方程的关系的过程,体会数形结合思想,感受数学的严谨性及数学结论的确定性,提高学生的估算能力.
3.培养学生独立思考的习惯与合作交流的意识,激发学生的学习兴趣,体验探索成功后的快乐.
二、教学重难点
1. 教学重点
体会方程与函数之间的联系,能够利用二次函数的图象求一元二次方程的近似解
2. 教学难点
探索方程与函数之间联系的过程,理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系和数形结合思想的运用.
三、教学过程
(一)新课导入
教师提问,引入新课
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:,你能否解决以下问题:
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
(2)球从飞出到落地要用多少时间?
现在不能解决也不要紧,学完本课,你就会清楚了.
(二)探索新知
思考
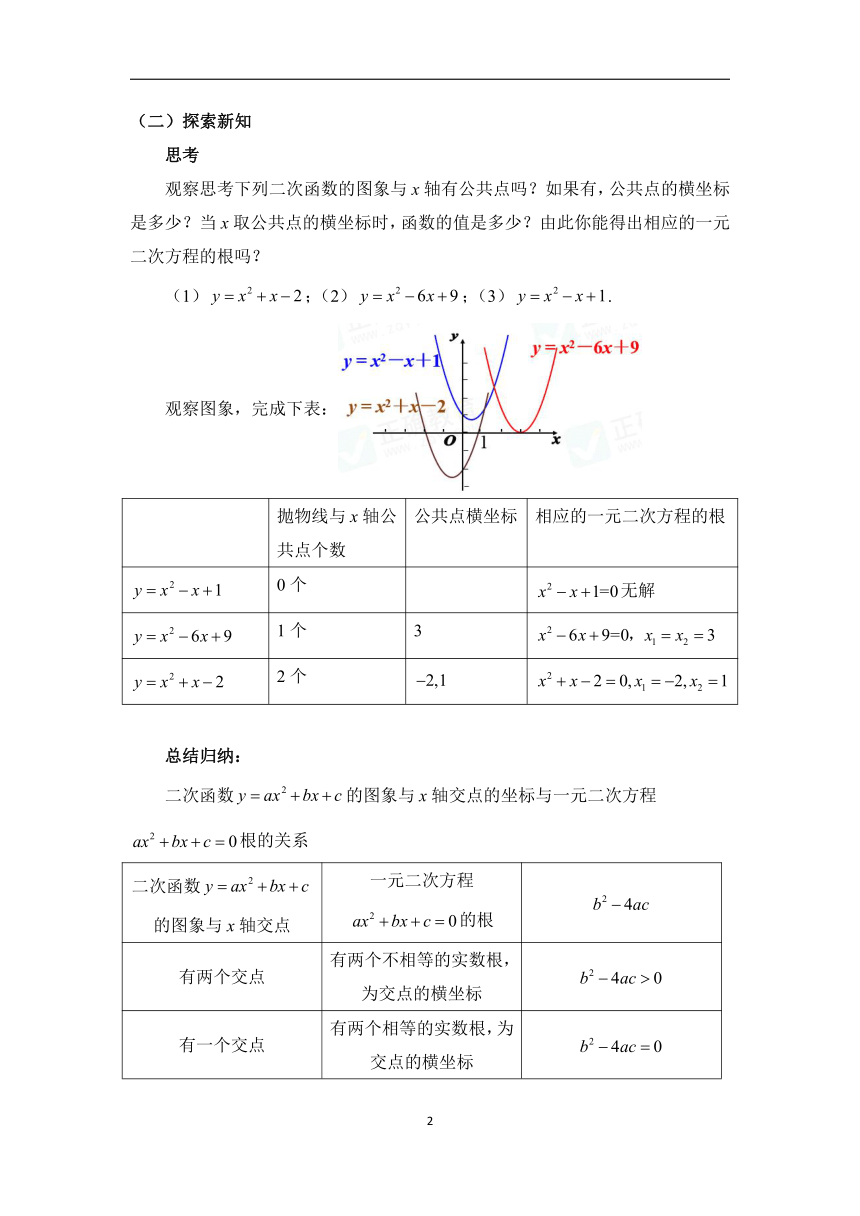
观察思考下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数的值是多少?由此你能得出相应的一元二次方程的根吗?
(1);(2);(3).
观察图象,完成下表:
抛物线与x轴公共点个数 公共点横坐标 相应的一元二次方程的根
0个 无解
1个 3
2个
总结归纳:
二次函数的图象与x轴交点的坐标与一元二次方程根的关系
二次函数的图象与x轴交点 一元二次方程的根
有两个交点 有两个不相等的实数根,为交点的横坐标
有一个交点 有两个相等的实数根,为交点的横坐标
没有交点 没有实数根
问题 如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:,你能否解决以下问题:
分析:由于小球的飞行高度h与飞行时间t有函数关系,所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程.如果方程有合乎实际的解,则说明小球的飞行高度可以达到问题中h的值;否则,说明小球的飞行高度不能达到问题中h的值.
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
解方程:,
,
.
所以当球飞行1s或3s时,它的高度为15m.
(2)球从飞出到落地要用多少时间?
解方程:,
,
.
当小球飞行2s时,它的高度为20m.
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
解方程:,.
因为,所以方程无实数根.这就是说,小球的飞行高度达不到20.5m.
(4)球从飞出到落地要用多少时间?
,,.
当球飞行0s和4s时,它的高度为0m.
即0s时球从地面飞出,4s时球落回地面.
提问:从上面发现,二次函数何时为一元二次方程?
一般地,当y取定值且时,二次函数为一元二次方程.
所以二次函数与一元二次方程关系密切.
例如,已知二次函数的值为3,求自变量x的值,可以解一元二次方程(即).
反过来,解方程又可以看作已知二次函数的值为0,求自变量x的值.
探究 利用图象法求一元二次方程的近似根
求一元二次方程的近似根(精确到0.1)
分析:一元二次方程的根就是抛物线与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.
解:画出函数的图象(如下图),由图象可知,方程有两个实数根,一个在与0之间,另一个在2与3之间.
先求位于到0之间的根,由图象可估计这个根是或,利用计算器进行探索,见下表:
观察上表可以发现,当x分别取和时,对应的y由负变正,可见在与之间肯定有一个x使y=0,即有的一个根,题目只要求精确到0.1,这时取或都符合要求.但当时更为接近0.故.
同理可得另一近似值为.
归纳:利用图象法一元二次方程的近似根
(1)用描点法作二次函数的图象;
(2)观察估计二次函数的图象与x轴的交点的横坐标;
(可将单位长度十等分,借助计算器确定其近似值)
(3)确定方程的近似根.
典例
例1 已知二次函数的图象如图所示,则一元二次方程的近似根( )
A. B.
C. D.
解析:由图象可得二次函数图象的对称轴为,而对称轴右侧图象与x轴交点到原点的距离约为0.5,;又∵对称轴为,则,.故,.故选B.
方法总结:解答本题首先需要根据图象估计出一个根,再根据对称性计算出另一个根,估计值的精确程度,直接关系到计算的准确性,故估计要准确.
练习
1.下表是二次函数(,a,b,c为常数)的自变量x与函数值y的部分对应值.判断方程的一个根的取值范围是( )
x 6.17 6.18 6.19 6.20
-0.11 -0.04 0.01 0.04
A. B.
C. D.
答案:C
解析:当时,,当时,,
方程的一个根的取值范围是,故选C.
2.若抛物线与x轴没有交点,请你写出一个符合条件的m值,____________.
答案:10(答案不唯一)
解析:抛物线与x轴没有交点
,
解得:,
取.
3.二次函数的解析式为.
(1)求证:无论m取何值,抛物线总与x轴有交点;
(2)当时,求抛物线与x轴的两个交点的坐标.
解析:(1)证明:令
,,,
方程总有实数根
抛物线与x轴总有交点
(2)当时
令,
解得,
交点为或
(三)小结作业
小结:
1.本节课我们主要学习了哪些内容?
2.二次函数与一元二次方程的关系
3.利用函数图象探索一元二次方程的根
作业:
四、板书设计
22.2二次函数与一元二次方程
探究一:二次函数图象与x轴交点个数和一元二次方程根的关系
探究二:利用图象法求一元二次方程的近似根
练习
2
22.2二次函数与一元二次方程
教学设计
一、教学目标
1.了解一元二次方程的根的几何意义,知道抛物线与x轴的三种位置关系对应着一元二次方程的根的三种情况,会利用二次函数的图象求一元二次方程的近似解.
2.通过探索二次函数与一元二次方程的关系的过程,体会数形结合思想,感受数学的严谨性及数学结论的确定性,提高学生的估算能力.
3.培养学生独立思考的习惯与合作交流的意识,激发学生的学习兴趣,体验探索成功后的快乐.
二、教学重难点
1. 教学重点
体会方程与函数之间的联系,能够利用二次函数的图象求一元二次方程的近似解
2. 教学难点
探索方程与函数之间联系的过程,理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系和数形结合思想的运用.
三、教学过程
(一)新课导入
教师提问,引入新课
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:,你能否解决以下问题:
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
(2)球从飞出到落地要用多少时间?
现在不能解决也不要紧,学完本课,你就会清楚了.
(二)探索新知
思考
观察思考下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数的值是多少?由此你能得出相应的一元二次方程的根吗?
(1);(2);(3).
观察图象,完成下表:
抛物线与x轴公共点个数 公共点横坐标 相应的一元二次方程的根
0个 无解
1个 3
2个
总结归纳:
二次函数的图象与x轴交点的坐标与一元二次方程根的关系
二次函数的图象与x轴交点 一元二次方程的根
有两个交点 有两个不相等的实数根,为交点的横坐标
有一个交点 有两个相等的实数根,为交点的横坐标
没有交点 没有实数根
问题 如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:,你能否解决以下问题:
分析:由于小球的飞行高度h与飞行时间t有函数关系,所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程.如果方程有合乎实际的解,则说明小球的飞行高度可以达到问题中h的值;否则,说明小球的飞行高度不能达到问题中h的值.
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
解方程:,
,
.
所以当球飞行1s或3s时,它的高度为15m.
(2)球从飞出到落地要用多少时间?
解方程:,
,
.
当小球飞行2s时,它的高度为20m.
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
解方程:,.
因为,所以方程无实数根.这就是说,小球的飞行高度达不到20.5m.
(4)球从飞出到落地要用多少时间?
,,.
当球飞行0s和4s时,它的高度为0m.
即0s时球从地面飞出,4s时球落回地面.
提问:从上面发现,二次函数何时为一元二次方程?
一般地,当y取定值且时,二次函数为一元二次方程.
所以二次函数与一元二次方程关系密切.
例如,已知二次函数的值为3,求自变量x的值,可以解一元二次方程(即).
反过来,解方程又可以看作已知二次函数的值为0,求自变量x的值.
探究 利用图象法求一元二次方程的近似根
求一元二次方程的近似根(精确到0.1)
分析:一元二次方程的根就是抛物线与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.
解:画出函数的图象(如下图),由图象可知,方程有两个实数根,一个在与0之间,另一个在2与3之间.
先求位于到0之间的根,由图象可估计这个根是或,利用计算器进行探索,见下表:
观察上表可以发现,当x分别取和时,对应的y由负变正,可见在与之间肯定有一个x使y=0,即有的一个根,题目只要求精确到0.1,这时取或都符合要求.但当时更为接近0.故.
同理可得另一近似值为.
归纳:利用图象法一元二次方程的近似根
(1)用描点法作二次函数的图象;
(2)观察估计二次函数的图象与x轴的交点的横坐标;
(可将单位长度十等分,借助计算器确定其近似值)
(3)确定方程的近似根.
典例
例1 已知二次函数的图象如图所示,则一元二次方程的近似根( )
A. B.
C. D.
解析:由图象可得二次函数图象的对称轴为,而对称轴右侧图象与x轴交点到原点的距离约为0.5,;又∵对称轴为,则,.故,.故选B.
方法总结:解答本题首先需要根据图象估计出一个根,再根据对称性计算出另一个根,估计值的精确程度,直接关系到计算的准确性,故估计要准确.
练习
1.下表是二次函数(,a,b,c为常数)的自变量x与函数值y的部分对应值.判断方程的一个根的取值范围是( )
x 6.17 6.18 6.19 6.20
-0.11 -0.04 0.01 0.04
A. B.
C. D.
答案:C
解析:当时,,当时,,
方程的一个根的取值范围是,故选C.
2.若抛物线与x轴没有交点,请你写出一个符合条件的m值,____________.
答案:10(答案不唯一)
解析:抛物线与x轴没有交点
,
解得:,
取.
3.二次函数的解析式为.
(1)求证:无论m取何值,抛物线总与x轴有交点;
(2)当时,求抛物线与x轴的两个交点的坐标.
解析:(1)证明:令
,,,
方程总有实数根
抛物线与x轴总有交点
(2)当时
令,
解得,
交点为或
(三)小结作业
小结:
1.本节课我们主要学习了哪些内容?
2.二次函数与一元二次方程的关系
3.利用函数图象探索一元二次方程的根
作业:
四、板书设计
22.2二次函数与一元二次方程
探究一:二次函数图象与x轴交点个数和一元二次方程根的关系
探究二:利用图象法求一元二次方程的近似根
练习
2
同课章节目录
