22.1.4.1 二次函数y=ax?+bx+c的图象和性质 学案(含解析)
文档属性
| 名称 | 22.1.4.1 二次函数y=ax?+bx+c的图象和性质 学案(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 325.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 11:53:33 | ||
图片预览


文档简介
第二十二章 二次函数
22.1.4.1二次函数的图象和性质
学案
一、学习目标
1.会用配方法或公式法将一般式化成顶点式.
2.会熟练求出二次函数一般式的顶点坐标,对称轴等性质
二、基础知识
1.我们如何用配方法将一般式化成顶点式?
.
2.抛物线的顶点坐标是:.
对称轴是:直线
如果,当时,y随x的增大而减小;当时,y随x的增大而增大;
如果,当时,y随x的增大而增大;当时,y随x的增大而减小.
3.二次函数的图象与系数的关系
①a决定开口方向:开口向上;开口向下;
②同号对称轴在y轴的左侧;异号对称轴在y轴的右侧;
③经过原点;与y轴的交点位于x轴的上方;与y轴的交点位于x轴的下方;
④当时,y的值为,当时,y的值为.
⑤当对称轴时,,,此时;
当对称轴时,,,此时.
因此,判断的符号,需判断对称轴与1的大小,若对称轴在直线的左边,则,再根据a的符号即可得出结果;判断的符号,同理需判断对称轴与的大小.
三、巩固练习
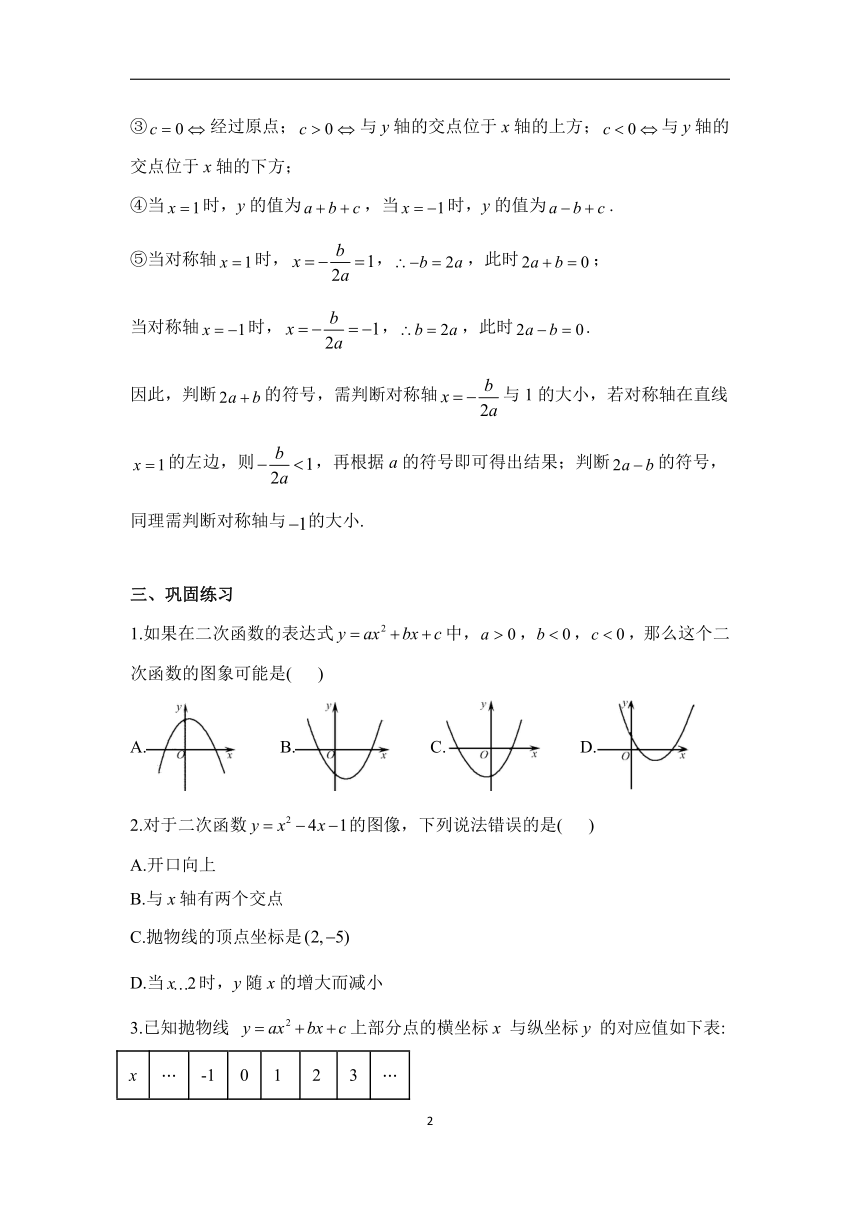
1.如果在二次函数的表达式中,,,,那么这个二次函数的图象可能是( )
A. B. C. D.
2.对于二次函数的图像,下列说法错误的是( )
A.开口向上
B.与x轴有两个交点
C.抛物线的顶点坐标是
D.当时,y随x的增大而减小
3.已知抛物线 上部分点的横坐标x 与纵坐标y 的对应值如下表:
x -1 0 1 2 3
y 3 0 -1 m 3
以下结论中错误的是
A. 抛物线开口向上 B. 抛物线的对称轴为直线
C. m的值为 0 D. 图象不经过第三象限
4.在平面直角坐标系中,二次函数的图象如图所示,则下列结论正确的( )
A. B. C. D.
5.将抛物线向左平移2个单位长度,所得抛物线为__________.
6.已知点,是抛物线 上的两点, 则m,n的大小关系为_______.
7.在二次函数的图象中,若y随x的增大而减少,则x的取值范围是___________.
8.如图,抛物线与x轴相交于点,,与y轴相交于点C.
(1)求抛物线的解析式.
(2)点,是抛物线上不同的两点且,求的最小值.
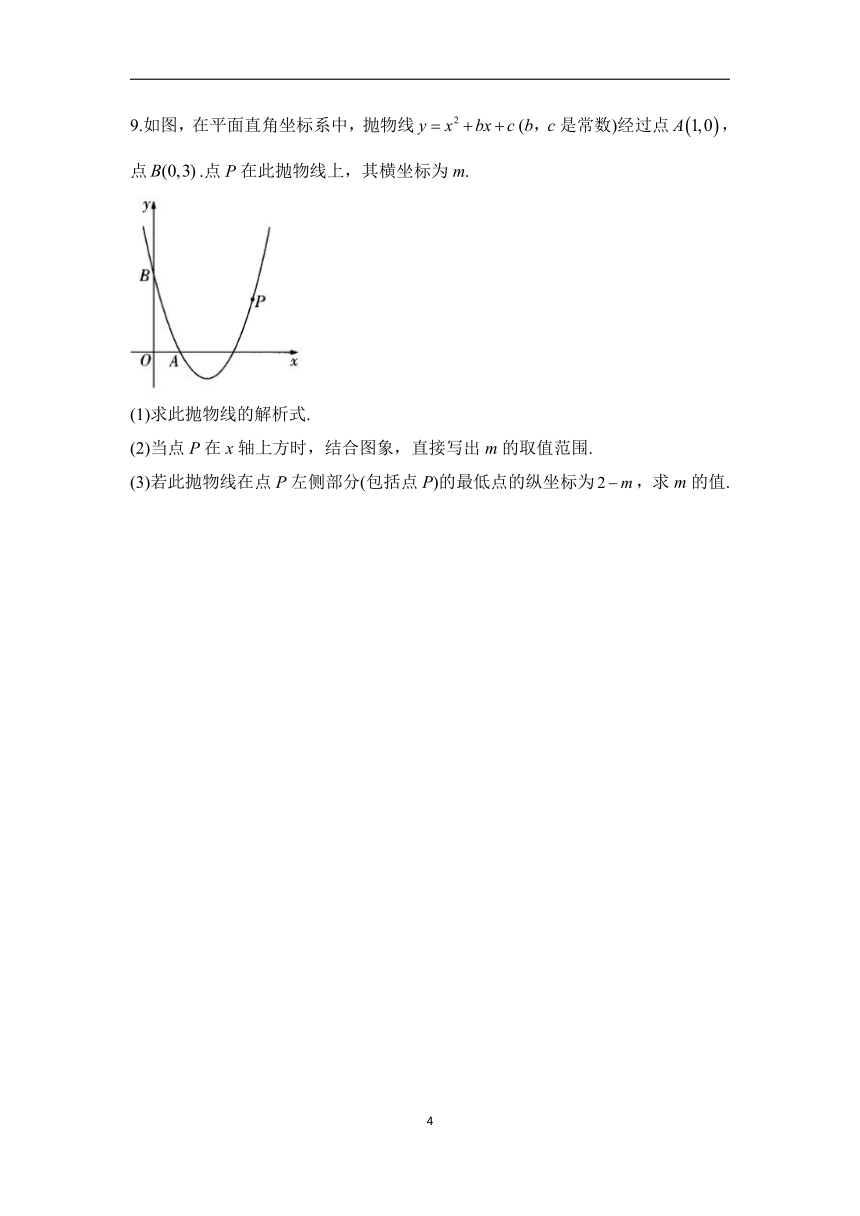
9.如图,在平面直角坐标系中,抛物线(b,c是常数)经过点,点.点P在此抛物线上,其横坐标为m.
(1)求此抛物线的解析式.
(2)当点P在x轴上方时,结合图象,直接写出m的取值范围.
(3)若此抛物线在点P左侧部分(包括点P)的最低点的纵坐标为,求m的值.
答案
巩固练习
1.答案:B
解析:由,,,推出,可知抛物线的图象开口向上,对称轴在y轴的右边,交y轴于负半轴,由此即可判断。
,,,
,
抛物线的图象开口向上,对称轴在y轴的右边,交y轴于负半轴.故选B.
2.答案:D
解析:A.二次函数中,,则,
抛物线开口向上,故选项正确,不符合题意;
B.当时,,
对于方程来说,
,
方程有两个不相等的实数根,则二次函数的图像
与x轴有两个交点,故选项正确,不符合题意;
C.,
抛物线的顶点坐标是,故选项正确,不符合题意;
D.,
抛物线的对称轴是,
,
抛物线开口向上,
当时,y随x的增大而增大,故选项错误,符合题意.故选D.
3.答案:B
解析:由表格中数据可知, 当或3时, 3 , 故抛物线的对称轴是直线. 点关于抛物线的对称轴的对称点为点, 即抛物线一定经过点, 故. 描点画出大致图象可知, 该拋物线开口向上, 且不经过第三象限. 故选B.
4.答案:C
解析:A.由抛物线的开口方向向下知,抛物线与y轴交于负半轴知,则,故本选项错误;
B.由抛物线与x轴有两个交点知,故本选项错误;
C.由抛物线图的轴对称性质知,抛物线与x轴的另一个交点坐标是点,所以当时,,即,本选项结论正确;
D.由图象可得:对称轴是直线,即,故本选项结论错误;
故选C.
5.答案:
解析:将抛物线向左平移2个单位长度得到抛物线,故答案为.
6.答案:
解析:易知抛物线 的对称轴为直线, 点A到对称轴的距离为 2 , 点B到对称轴的距离为1,,抛物线开口向上, 抛物线上 的点到对称轴的距离越小, 点的纵坐标越小,.
7.答案:
解析:二次函数解析式为,
二次函数对称轴为直线,开口向下,
当时,y随x的增大而减少,
故答案为:.
8.解析:(1)设抛物线的表达式为:,
由题意可得:,,
,
,解得:,
故抛物线的表达式为:;
(2)由抛物线的表达式知,抛物线的对称轴为直线,
①若点M、N关于抛物线对称轴对称,则,,
②,
,
,
即的最小值为.
9.解析:(1)将,分别代入,
得解得
故此抛物线的解析式为.
(2)对于,
当时,,解得或,
则此抛物线与x轴的另一个交点坐标为.
结合图象可知,当点P在x轴上方时,m的取值范围为或.
(3)易知抛物线的对称轴为直线,顶点坐标为,.
分以下2种情况讨论.
i.当时,最低点的纵坐标为,
令,
解得,(不合题意,舍去).
ii.当时,最低点的纵坐标为-1,
令,
解得.
综上所述,m的值为或3.
2
22.1.4.1二次函数的图象和性质
学案
一、学习目标
1.会用配方法或公式法将一般式化成顶点式.
2.会熟练求出二次函数一般式的顶点坐标,对称轴等性质
二、基础知识
1.我们如何用配方法将一般式化成顶点式?
.
2.抛物线的顶点坐标是:.
对称轴是:直线
如果,当时,y随x的增大而减小;当时,y随x的增大而增大;
如果,当时,y随x的增大而增大;当时,y随x的增大而减小.
3.二次函数的图象与系数的关系
①a决定开口方向:开口向上;开口向下;
②同号对称轴在y轴的左侧;异号对称轴在y轴的右侧;
③经过原点;与y轴的交点位于x轴的上方;与y轴的交点位于x轴的下方;
④当时,y的值为,当时,y的值为.
⑤当对称轴时,,,此时;
当对称轴时,,,此时.
因此,判断的符号,需判断对称轴与1的大小,若对称轴在直线的左边,则,再根据a的符号即可得出结果;判断的符号,同理需判断对称轴与的大小.
三、巩固练习
1.如果在二次函数的表达式中,,,,那么这个二次函数的图象可能是( )
A. B. C. D.
2.对于二次函数的图像,下列说法错误的是( )
A.开口向上
B.与x轴有两个交点
C.抛物线的顶点坐标是
D.当时,y随x的增大而减小
3.已知抛物线 上部分点的横坐标x 与纵坐标y 的对应值如下表:
x -1 0 1 2 3
y 3 0 -1 m 3
以下结论中错误的是
A. 抛物线开口向上 B. 抛物线的对称轴为直线
C. m的值为 0 D. 图象不经过第三象限
4.在平面直角坐标系中,二次函数的图象如图所示,则下列结论正确的( )
A. B. C. D.
5.将抛物线向左平移2个单位长度,所得抛物线为__________.
6.已知点,是抛物线 上的两点, 则m,n的大小关系为_______.
7.在二次函数的图象中,若y随x的增大而减少,则x的取值范围是___________.
8.如图,抛物线与x轴相交于点,,与y轴相交于点C.
(1)求抛物线的解析式.
(2)点,是抛物线上不同的两点且,求的最小值.
9.如图,在平面直角坐标系中,抛物线(b,c是常数)经过点,点.点P在此抛物线上,其横坐标为m.
(1)求此抛物线的解析式.
(2)当点P在x轴上方时,结合图象,直接写出m的取值范围.
(3)若此抛物线在点P左侧部分(包括点P)的最低点的纵坐标为,求m的值.
答案
巩固练习
1.答案:B
解析:由,,,推出,可知抛物线的图象开口向上,对称轴在y轴的右边,交y轴于负半轴,由此即可判断。
,,,
,
抛物线的图象开口向上,对称轴在y轴的右边,交y轴于负半轴.故选B.
2.答案:D
解析:A.二次函数中,,则,
抛物线开口向上,故选项正确,不符合题意;
B.当时,,
对于方程来说,
,
方程有两个不相等的实数根,则二次函数的图像
与x轴有两个交点,故选项正确,不符合题意;
C.,
抛物线的顶点坐标是,故选项正确,不符合题意;
D.,
抛物线的对称轴是,
,
抛物线开口向上,
当时,y随x的增大而增大,故选项错误,符合题意.故选D.
3.答案:B
解析:由表格中数据可知, 当或3时, 3 , 故抛物线的对称轴是直线. 点关于抛物线的对称轴的对称点为点, 即抛物线一定经过点, 故. 描点画出大致图象可知, 该拋物线开口向上, 且不经过第三象限. 故选B.
4.答案:C
解析:A.由抛物线的开口方向向下知,抛物线与y轴交于负半轴知,则,故本选项错误;
B.由抛物线与x轴有两个交点知,故本选项错误;
C.由抛物线图的轴对称性质知,抛物线与x轴的另一个交点坐标是点,所以当时,,即,本选项结论正确;
D.由图象可得:对称轴是直线,即,故本选项结论错误;
故选C.
5.答案:
解析:将抛物线向左平移2个单位长度得到抛物线,故答案为.
6.答案:
解析:易知抛物线 的对称轴为直线, 点A到对称轴的距离为 2 , 点B到对称轴的距离为1,,抛物线开口向上, 抛物线上 的点到对称轴的距离越小, 点的纵坐标越小,.
7.答案:
解析:二次函数解析式为,
二次函数对称轴为直线,开口向下,
当时,y随x的增大而减少,
故答案为:.
8.解析:(1)设抛物线的表达式为:,
由题意可得:,,
,
,解得:,
故抛物线的表达式为:;
(2)由抛物线的表达式知,抛物线的对称轴为直线,
①若点M、N关于抛物线对称轴对称,则,,
②,
,
,
即的最小值为.
9.解析:(1)将,分别代入,
得解得
故此抛物线的解析式为.
(2)对于,
当时,,解得或,
则此抛物线与x轴的另一个交点坐标为.
结合图象可知,当点P在x轴上方时,m的取值范围为或.
(3)易知抛物线的对称轴为直线,顶点坐标为,.
分以下2种情况讨论.
i.当时,最低点的纵坐标为,
令,
解得,(不合题意,舍去).
ii.当时,最低点的纵坐标为-1,
令,
解得.
综上所述,m的值为或3.
2
同课章节目录
