山东省泰安市青岛版九年级数学下册反比例函数对应练习题
文档属性
| 名称 | 山东省泰安市青岛版九年级数学下册反比例函数对应练习题 |
|
|
| 格式 | zip | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-08 00:00:00 | ||
图片预览




文档简介
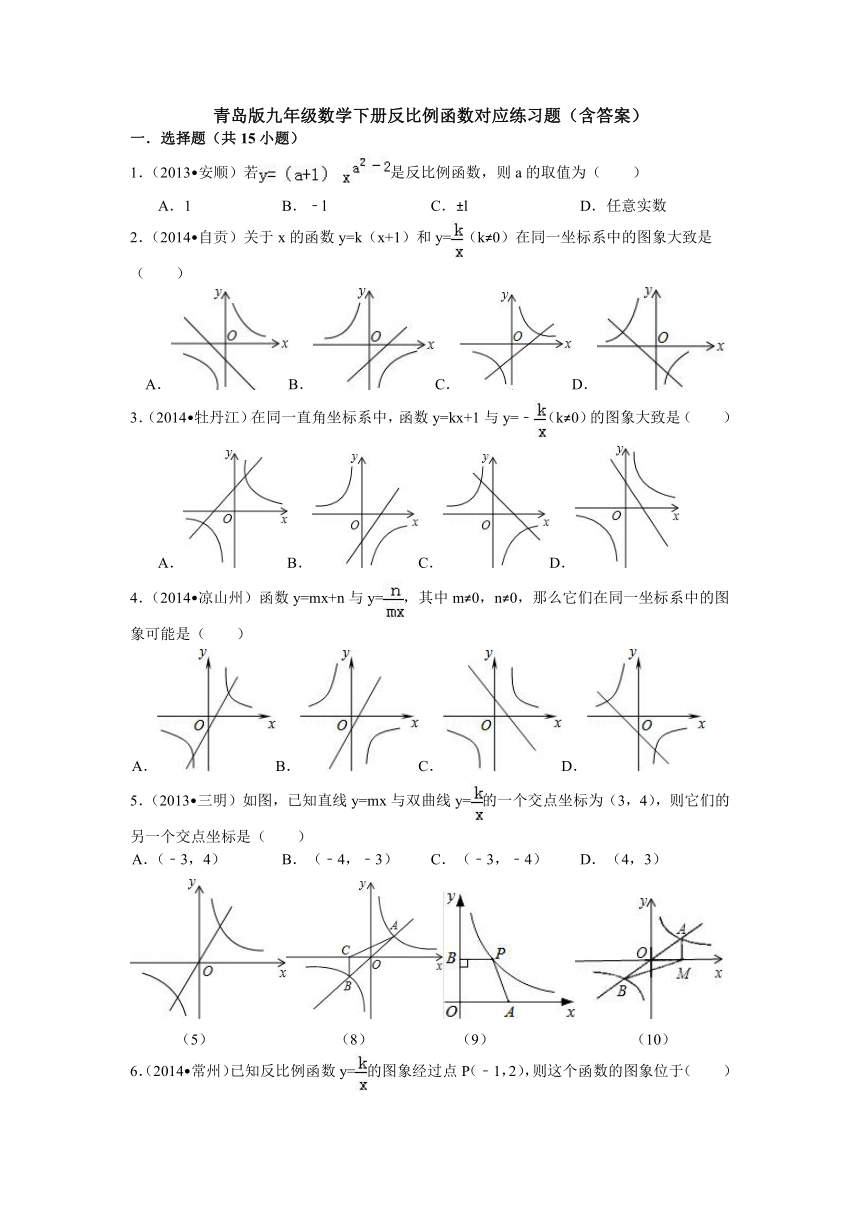
青岛版九年级数学下册反比例函数对应练习题(含答案)
一.选择题(共15小题)
1.(2013 安顺)若是反比例函数,则a的取值为( )
A.1 B. ﹣l C. ±l D. 任意实数
2.(2014 自贡)关于x的函数y=k(x+1)和y=(k≠0)在同一坐标系中的图象大致是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )
3.(2014 牡丹江)在同一直角坐标系中,函数y=kx+1与y=﹣(k≠0)的图象大致是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )
4.(2014 凉山州)函数y=mx+n与y=,其中m≠0,n≠0,那么它们在同一坐标系中的图象可能是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )
5.(2013 三明)如图,已知直线y=mx与双曲线y=的一个交点坐标为(3,4),则它们的另一个交点坐标是( )
A.(﹣3,4) B. (﹣4,﹣3) C. (﹣3,﹣4) D. (4,3)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(5) (8) (9) (10)
6.(2014 常州)已知反比例函数y=的图象经过点P(﹣1,2),则这个函数的图象位于( )
A.第二,三象限 B. 第一,三象限 C. 第三,四象限 D. 第二,四象限
7.(2014 兰州)若反比例函数的图象位于第二、四象限,则k的取值可以是( )
A.0 B. 1 C. 2 D. 以上都不是
8.(2014 黔东南州)如图,正比例函数y=x与反比例函数y=的图象相交于A、B两点,BC⊥x轴于点C,则△ABC的面积为( )
A.1 B. 2 C. D.
9.(2014 抚顺)如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
A.逐渐增大 B. 不变 C. 逐渐减小 D. 先增大后减小
10.(2014 鄂州一模)如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是( )
A.2 B. m﹣2 C. m D. 4
11.(2014 宁夏)已知两点P1(x1,y1)、P2(x2,y2)在函数y=的图象上,当x1>x2>0时,下列结论正确的是( )
A.0<y1<y2 B. 0<y2<y1 C. y1<y2<0 D. y2<y1<0
12.(2014 咸宁)如图,双曲线y=与直线y=kx+b交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为﹣1.根据图象信息可得关于x的方程=kx+b的解为( )
A.﹣3,1 B. ﹣3,3 C. ﹣1,1 D. ﹣1,3
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(12) (13) (14)
13.(2014 聊城)如图,一次函数y1=k1x+b的图象和反比例函数y2=的图象交于A(1,2),B(﹣2,﹣1)两点,若y1<y2,则x的取值范围是( )
A.x<1 B. x<﹣2 C. ﹣2<x<0或x>1 D. x<﹣2或0<x<1
14.(2014 黔西南州)已知如图,一次函数y=ax+b和反比例函数y=的图象相交于A、B两点,不等式ax+b>的解集为( )
A.x<﹣3 B. ﹣3<x<0或x>1 C. x<﹣3或x>1 D. ﹣3<x<1
15.(2014 嘉定区二模)已知矩形的面积为20,则如图给出的四个图象中,能大致呈现矩形的长y与宽x之间的函数关系的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二.填空题(共5小题)
16.(2014 贵阳)若反比例函数的图象在其每个象限内,y随x的增大而增大,则k的值可以是 _________ .(写出一个符合条件的值即可)
17.(2014 崇左)如图,A(4,0 ( http: / / www.21cnjy.com )),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为 _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(17) (18) (19) (20)
18.(2014 黔南州)如图,正比例函数y1=k1x与反比例函数y2=的图象交于A、B两点,根据图象可直接写出当y1>y2时,x的取值范围是 _________ .
19.(2014 赤峰)如图,反比例函数y=(k>0)的图象与以原点(0,0)为圆心的圆交于A,B两点,且A(1,),图中阴影部分的面积等于 _________ .(结果保留π)
20.(2014 临沂)如图,反比例函数y=的图象经过Rt△OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为 _________ .
三.解答题(共5小题)
21.(2014 遂宁)已知:如图,反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
( http: / / www.21cnjy.com )
22.(2014 烟台)如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
( http: / / www.21cnjy.com )
23.(2014 呼伦贝尔)如图,在平面直角坐标系xOy中,已知一次函数y=kx+b的图象经过点A(1,0),与反比例函数(x>0)的图象相交于点B(2,1).
(1)求m的值和一次函数的解析式;
(2)结合图象直接写出:当x>0时,不等式的解集.
( http: / / www.21cnjy.com )
24.(2014 安顺)如图,点A(m,m+1),B(m+3,m﹣1)是反比例函数(x>0)与一次函数y=ax+b的交点.求:
(1)反比例函数与一次函数的解析式;
(2)根据图象直接写出当反比例函数的函数值大于一次函数的函数值时x的取值范围.
( http: / / www.21cnjy.com )
25.(2014 兴化市二模)如图所示,制 ( http: / / www.21cnjy.com )作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
(1)分别求出该材料加热和停止加热过程中y与x的函数关系式(写出x的取值范围);
(2)根据该食品制作要求,在材料温度不低于12℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
( http: / / www.21cnjy.com )
参考答案
一.选择题(共15小题)
1.A.2.D.3.D.4.B.5.C.6.D.7.A.8.A.9.C.10.A.11.A.12.A.
13.D.14.B.15.A.
二.填空题(共5小题)
16. ﹣1(答案不唯一) .17. y=﹣ .18. ﹣1<x<0或x>1
19. .20. y= .
三.解答题(共5小题)
21.解:(1)把A点(1,4)分别代入反比例函数y=,一次函数y=x+b,得k=1×4,1+b=4,
解得k=4,b=3,
∴反比例函数的解析式是y=,一次函数解析式是y=x+3;
(2)如图,设直线y=x+3与y轴的交点为C,
当x=﹣4时,y=﹣1,
∴B(﹣4,﹣1),
当x=0时,y=+3,
∴C(0,3),
∴S△AOB=S△AOC+S△BOC==;
(3)∵B(﹣4,﹣1),A(1,4),
∴根据图象可知:当x>1或﹣4<x<0时,一次函数值大于反比例函数值.
( http: / / www.21cnjy.com )
22.解:(1)由题意得:,
解得:,
∴A(1,6),B(6,1),
设反比例函数解析式为y=,
将A(1,6)代入得:k=6,
则反比例解析式为y=;
(2)存在,
设E(x,0),则DE=x﹣1,CE=6﹣x,
∵AD⊥x轴,BC⊥x轴,
∴∠ADE=∠BCE=90°,
连接AE,BE,
则S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE
=(BC+AD) DC﹣DE AD﹣CE BC
=×(1+6)×5﹣(x﹣1)×6﹣(6﹣x)×1
=﹣x=5,
解得:x=5,
则E(5,0).
( http: / / www.21cnjy.com )
23.解:(1)∵反比例函数y=(x>0)的图象经过点B(2,1),
∴将B坐标代入反比例解析式得:m=1×2=2,
∵一次函数y=kx+b的图象经过点A(1,0)、B(2,1)两点,
∴将A和B坐标代入一次函数解析式得:,
解得:,
∴一次函数的解析式为y=x﹣1;
(2)由图象可知:当x>0时,不等式kx+b>的解集为x>2.
24.解:(1)由题意可知,m(m+1)=(m+3)(m﹣1).
解,得m=3.(2分)
∴A(3,4),B(6,2);
∴k=4×3=12,
∴.(3分)
∵A点坐标为(3,4),B点坐标为(6,2),
∴,
∴,
∴y=﹣x+6.(5分)
(2)根据图象得x的取值范围:0<x<3或x>6.(
25.解:(1)设加热停止后反比例函数表达式为y=,
∵y=过(12,14),得k1=12×14=168,
则y=;
当y=28时,28=,得x=6.
设加热过程中一次函数表达式y=k2x+b,
由图象知y=k2x+b过点(0,4)与(6,28),
∴,
解得,
∴y=4x+4,此时x的范围是0≤x≤6.
y=此时x的范围是x>6;
(2)当y=12时,由y=4x+4,
得x=2.
由y=,
得x=14,
所以对该材料进行特殊处理所用的时间为14﹣2=12(分钟).
一.选择题(共15小题)
1.(2013 安顺)若是反比例函数,则a的取值为( )
A.1 B. ﹣l C. ±l D. 任意实数
2.(2014 自贡)关于x的函数y=k(x+1)和y=(k≠0)在同一坐标系中的图象大致是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )
3.(2014 牡丹江)在同一直角坐标系中,函数y=kx+1与y=﹣(k≠0)的图象大致是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )
4.(2014 凉山州)函数y=mx+n与y=,其中m≠0,n≠0,那么它们在同一坐标系中的图象可能是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )
5.(2013 三明)如图,已知直线y=mx与双曲线y=的一个交点坐标为(3,4),则它们的另一个交点坐标是( )
A.(﹣3,4) B. (﹣4,﹣3) C. (﹣3,﹣4) D. (4,3)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(5) (8) (9) (10)
6.(2014 常州)已知反比例函数y=的图象经过点P(﹣1,2),则这个函数的图象位于( )
A.第二,三象限 B. 第一,三象限 C. 第三,四象限 D. 第二,四象限
7.(2014 兰州)若反比例函数的图象位于第二、四象限,则k的取值可以是( )
A.0 B. 1 C. 2 D. 以上都不是
8.(2014 黔东南州)如图,正比例函数y=x与反比例函数y=的图象相交于A、B两点,BC⊥x轴于点C,则△ABC的面积为( )
A.1 B. 2 C. D.
9.(2014 抚顺)如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
A.逐渐增大 B. 不变 C. 逐渐减小 D. 先增大后减小
10.(2014 鄂州一模)如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是( )
A.2 B. m﹣2 C. m D. 4
11.(2014 宁夏)已知两点P1(x1,y1)、P2(x2,y2)在函数y=的图象上,当x1>x2>0时,下列结论正确的是( )
A.0<y1<y2 B. 0<y2<y1 C. y1<y2<0 D. y2<y1<0
12.(2014 咸宁)如图,双曲线y=与直线y=kx+b交于点M、N,并且点M的坐标为(1,3),点N的纵坐标为﹣1.根据图象信息可得关于x的方程=kx+b的解为( )
A.﹣3,1 B. ﹣3,3 C. ﹣1,1 D. ﹣1,3
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(12) (13) (14)
13.(2014 聊城)如图,一次函数y1=k1x+b的图象和反比例函数y2=的图象交于A(1,2),B(﹣2,﹣1)两点,若y1<y2,则x的取值范围是( )
A.x<1 B. x<﹣2 C. ﹣2<x<0或x>1 D. x<﹣2或0<x<1
14.(2014 黔西南州)已知如图,一次函数y=ax+b和反比例函数y=的图象相交于A、B两点,不等式ax+b>的解集为( )
A.x<﹣3 B. ﹣3<x<0或x>1 C. x<﹣3或x>1 D. ﹣3<x<1
15.(2014 嘉定区二模)已知矩形的面积为20,则如图给出的四个图象中,能大致呈现矩形的长y与宽x之间的函数关系的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二.填空题(共5小题)
16.(2014 贵阳)若反比例函数的图象在其每个象限内,y随x的增大而增大,则k的值可以是 _________ .(写出一个符合条件的值即可)
17.(2014 崇左)如图,A(4,0 ( http: / / www.21cnjy.com )),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为 _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(17) (18) (19) (20)
18.(2014 黔南州)如图,正比例函数y1=k1x与反比例函数y2=的图象交于A、B两点,根据图象可直接写出当y1>y2时,x的取值范围是 _________ .
19.(2014 赤峰)如图,反比例函数y=(k>0)的图象与以原点(0,0)为圆心的圆交于A,B两点,且A(1,),图中阴影部分的面积等于 _________ .(结果保留π)
20.(2014 临沂)如图,反比例函数y=的图象经过Rt△OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为 _________ .
三.解答题(共5小题)
21.(2014 遂宁)已知:如图,反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
( http: / / www.21cnjy.com )
22.(2014 烟台)如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
( http: / / www.21cnjy.com )
23.(2014 呼伦贝尔)如图,在平面直角坐标系xOy中,已知一次函数y=kx+b的图象经过点A(1,0),与反比例函数(x>0)的图象相交于点B(2,1).
(1)求m的值和一次函数的解析式;
(2)结合图象直接写出:当x>0时,不等式的解集.
( http: / / www.21cnjy.com )
24.(2014 安顺)如图,点A(m,m+1),B(m+3,m﹣1)是反比例函数(x>0)与一次函数y=ax+b的交点.求:
(1)反比例函数与一次函数的解析式;
(2)根据图象直接写出当反比例函数的函数值大于一次函数的函数值时x的取值范围.
( http: / / www.21cnjy.com )
25.(2014 兴化市二模)如图所示,制 ( http: / / www.21cnjy.com )作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
(1)分别求出该材料加热和停止加热过程中y与x的函数关系式(写出x的取值范围);
(2)根据该食品制作要求,在材料温度不低于12℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
( http: / / www.21cnjy.com )
参考答案
一.选择题(共15小题)
1.A.2.D.3.D.4.B.5.C.6.D.7.A.8.A.9.C.10.A.11.A.12.A.
13.D.14.B.15.A.
二.填空题(共5小题)
16. ﹣1(答案不唯一) .17. y=﹣ .18. ﹣1<x<0或x>1
19. .20. y= .
三.解答题(共5小题)
21.解:(1)把A点(1,4)分别代入反比例函数y=,一次函数y=x+b,得k=1×4,1+b=4,
解得k=4,b=3,
∴反比例函数的解析式是y=,一次函数解析式是y=x+3;
(2)如图,设直线y=x+3与y轴的交点为C,
当x=﹣4时,y=﹣1,
∴B(﹣4,﹣1),
当x=0时,y=+3,
∴C(0,3),
∴S△AOB=S△AOC+S△BOC==;
(3)∵B(﹣4,﹣1),A(1,4),
∴根据图象可知:当x>1或﹣4<x<0时,一次函数值大于反比例函数值.
( http: / / www.21cnjy.com )
22.解:(1)由题意得:,
解得:,
∴A(1,6),B(6,1),
设反比例函数解析式为y=,
将A(1,6)代入得:k=6,
则反比例解析式为y=;
(2)存在,
设E(x,0),则DE=x﹣1,CE=6﹣x,
∵AD⊥x轴,BC⊥x轴,
∴∠ADE=∠BCE=90°,
连接AE,BE,
则S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE
=(BC+AD) DC﹣DE AD﹣CE BC
=×(1+6)×5﹣(x﹣1)×6﹣(6﹣x)×1
=﹣x=5,
解得:x=5,
则E(5,0).
( http: / / www.21cnjy.com )
23.解:(1)∵反比例函数y=(x>0)的图象经过点B(2,1),
∴将B坐标代入反比例解析式得:m=1×2=2,
∵一次函数y=kx+b的图象经过点A(1,0)、B(2,1)两点,
∴将A和B坐标代入一次函数解析式得:,
解得:,
∴一次函数的解析式为y=x﹣1;
(2)由图象可知:当x>0时,不等式kx+b>的解集为x>2.
24.解:(1)由题意可知,m(m+1)=(m+3)(m﹣1).
解,得m=3.(2分)
∴A(3,4),B(6,2);
∴k=4×3=12,
∴.(3分)
∵A点坐标为(3,4),B点坐标为(6,2),
∴,
∴,
∴y=﹣x+6.(5分)
(2)根据图象得x的取值范围:0<x<3或x>6.(
25.解:(1)设加热停止后反比例函数表达式为y=,
∵y=过(12,14),得k1=12×14=168,
则y=;
当y=28时,28=,得x=6.
设加热过程中一次函数表达式y=k2x+b,
由图象知y=k2x+b过点(0,4)与(6,28),
∴,
解得,
∴y=4x+4,此时x的范围是0≤x≤6.
y=此时x的范围是x>6;
(2)当y=12时,由y=4x+4,
得x=2.
由y=,
得x=14,
所以对该材料进行特殊处理所用的时间为14﹣2=12(分钟).
