第三章 二次函数 阶段测试 二次函数的应用(含答案)
文档属性
| 名称 | 第三章 二次函数 阶段测试 二次函数的应用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 20:31:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章 二次函数
阶段测试 二次函数的应用
一、选择题(每题4分,共32分)
1.某农机厂四月份生产零件60万个,设该厂第二季度平均每月的增长率为x,如果第二季度共生产零件y万个,那么y与x满足的函数关系式是( )
A. y=60(1+x) B. y=60+60(1+x)+60(1+x)
C. y=60(1+x)+60(1+x) D. y=60+60(1+x)
2.某旅行社在“五一”期间接团去外地旅游,经计算,所获营业额y(元)与旅行团人数x(人)满足关系式y= -x +100x+28 400,要使所获营业额最大,则此旅行团应有( )
A.30人 B.40人 C.50人 D.55人
3.已知一个直角三角形两直角边长之和为20cm,则这个直角三角形的最大面积为( )
A.25 cm B.50 cm C.100 cm D.无法确定
4.当a≤x≤a+1时,函数y=x -2x+1的最小值为1,则a的值为( )
A.-1 B.2 C.0或2 D.-1或2
5.某产品进货单价为9元,按10元一件出售时,每天能售出50件.若每件每涨价1元,每天的销售量就减少10件,则销售该产品每天能获得的最大利润为( )
A.50元 B.80元 C.90元 D.100元
6.用总长为a米的材料做成如图①所示的矩形窗框,设窗框的宽为x米,窗框的面积为y平方米,y关于x的函数图象如图②,则a的值是( )
A.16 B.12 C.8 D.4
第6题图 第7题图
7.某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的关系如图所示,D为该水流的最高点,DA⊥OB,垂足为A.已知OC = OB =8m,OA=2m,则该水流距水平面的最大高度(AD的长度)为( )
A.9m B.10m C.11m D.12m
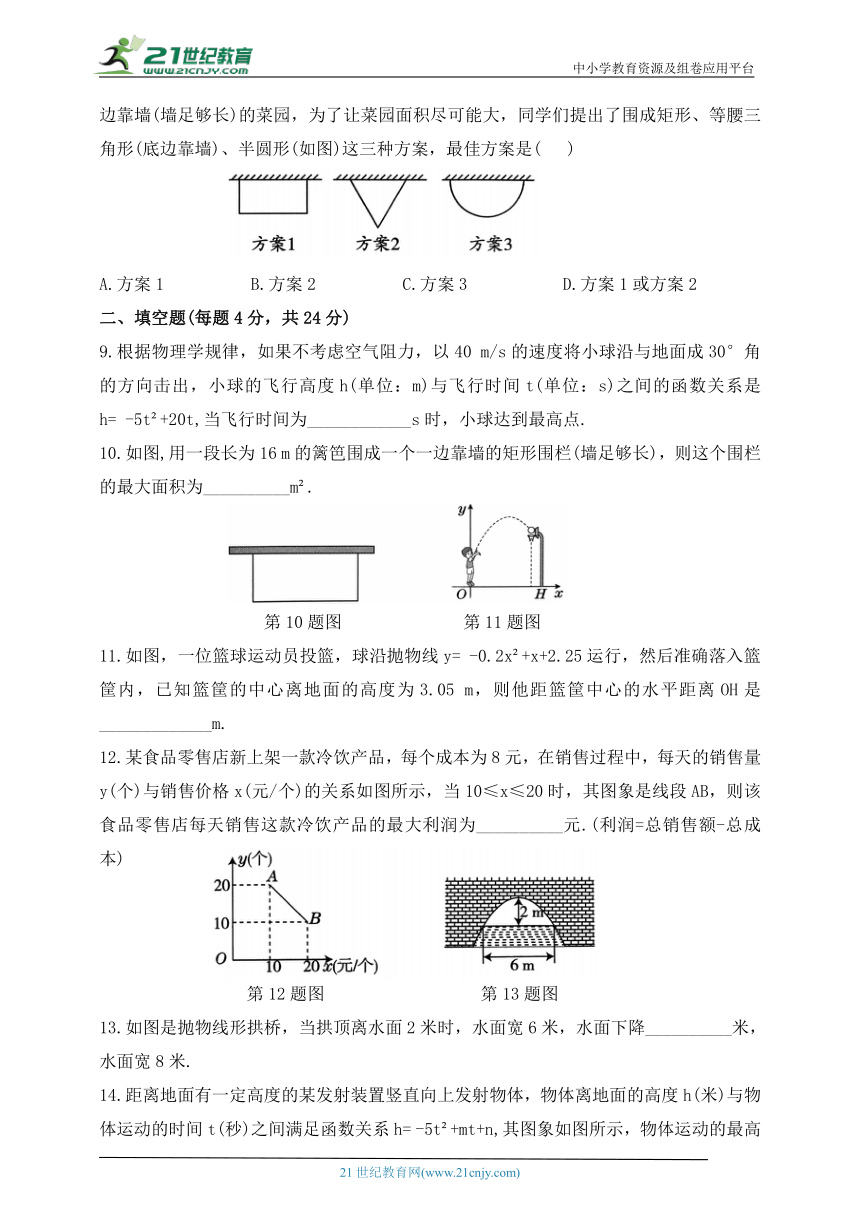
8.九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰三角形(底边靠墙)、半圆形(如图)这三种方案,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.方案1或方案2
二、填空题(每题4分,共24分)
9.根据物理学规律,如果不考虑空气阻力,以40 m/s的速度将小球沿与地面成30°角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是 h= -5t +20t,当飞行时间为____________s时,小球达到最高点.
10.如图,用一段长为16 m的篱笆围成一个一边靠墙的矩形围栏(墙足够长),则这个围栏的最大面积为__________m .
第10题图 第11题图
11.如图,一位篮球运动员投篮,球沿抛物线y= -0.2x +x+2.25运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为3.05 m,则他距篮筐中心的水平距离OH是_____________m.
12.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当10≤x≤20时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为__________元.(利润=总销售额-总成本)
第12题图 第13题图
13.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降__________米,水面宽8米.
14.距离地面有一定高度的某发射装置竖直向上发射物体,物体离地面的高度h(米)与物体运动的时间t(秒)之间满足函数关系h= -5t +mt+n,其图象如图所示,物体运动的最高点离地面20米,物体从发射到落地的运动时间为3秒,设w表示0秒到t秒时h的值的“极差”(即0秒到t秒时h的最大值与最小值的差),则当0≤t≤1时,w的取值范围是_______________;当2≤t≤3时,w的取值范围是____________.
三、解答题(共44分)
15.(10分)端午节前夕,某超市从厂家分两次购进A,B两种品牌的粽子,两次进货时,两种品牌粽子的进价不变.第一次购进A品牌粽子100袋和B品牌粽子150袋,总费用为7000元;第二次购进A品牌粽子180袋和B品牌粽子120袋,总费用为8100 元.
(1)求A,B两种品牌粽子每袋的进价各是多少元;
(2)当B品牌粽子销售价为每袋54元时,每天可售出20袋,为了促销,该超市决定对B品牌粽子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增
加5袋.当B品牌粽子每袋的销售价降低多少元时,每天售出B品牌粽子所获得的利润最大 最大利润是多少元
16.(10分)2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为x元时,求该商品销售量y与x之间的函数表达式;
(2)求每套售价定为多少元时,每天销售套件所获利润W最大,最大利润是多少元
17.(12分)2022 北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度OA为4米,以起跳点正下方跳台底端O为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点 B的坐标为(4,12),着陆坡顶端C与落地点D的距离为2.5米,若斜坡CD的坡度i=3:4(即
求:(1)点A 的坐标;
(2)该抛物线的函数表达式;
(3)起跳点A 与着陆坡顶端C之间的水平距离OC的长.(精确到0.1米)(参考数据: 1.73)
18.(12分)单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台.运动员起跳后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=a(x-h) +k(a<0).
某运动员进行了两次训练.
(1)第一次训练时,该运动员的水平距离x与竖直高度y的几组数据如下:
水平距离x/m 0 2 5 8 11 14
竖直高度y/m 20.00 21.40 22.75 23.20 22.75 21.40
根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系
(2)第二次训练时,该运动员的竖直高度y与水平距离x近似满足函数关系记该运动员第一次训练的着陆点的水平距离为 d ,第二次训练的着陆点的水平距离为d ,则 d _______d .(填“>”“=”或“<”)
参考答案
一、1. B 【点拨】该农机厂五月份生产零件( x)万个,六月份生产零件60(1+x) 万个.∵第二季度包括四月份、五月份和六月份,∴由“第二季度共生产零件y万个”可得y=60+60(1+x)+60(1+x) .
2. C 【点拨】y=-x +100x+28 400=-(x-50) +30900,当x=50时, 故选 C.
3. B 【点拨】设一条直角边为xcm,则另一条直角边为 50(cm ). ∴当x=10 时, 故选B.
4. D 【点拨】当y=1时,有x -2x+1=1,解得x =0,x =2.∵当a≤x≤a+1时,函数有最小值1,∴a=2或a+1=0,如图所示.∴a=2或a=-1,故选D.
5. C 【点拨】设销售单价定为x元,总利润为W元,则可得销量为[50-10(x-10)]件,单件利润为(x-9)元,由题意得,W=(x-9)[50-10(x-10)]=-10x +240x-1 350= -10(x-12) +90,故可得当x=12时,W取得最大值,为90.故选C.
6. B 【点拨】由图象可知,当x=2时,y有最大值,最大值为4,∴当x=2时,窗框的最大面积是4平方米,根据矩形面积计算公式,另一边为4÷2=2(米),∴材料总长为3×2+3×2=12(米).故选B.
7. A【点拨】根据题意,设抛物线的表达式为 y=a(x-2) +k,将点C(0,8)、B(8,0)的坐标代入,得 解得 抛物线的表达式为 .当x=2时,y=9,即AD=9m,故选A.
8. C 【点拨】如图,方案1:设AD=x米,则AB=(8-2x)米,则菜园面积为x(8-2x)=-2x +8x=-2·
(x-2) +8((平方米),当x=2时,此时菜园最大面积为8平方米.方案2:当∠BAC=90°时,菜园最大面积为 (平方米).方案3:易得半圆形的半径为米,此时菜园面积为 (平方米). .最佳方案是方案3.
二、9.2 【点拨】h=-5t +20t= -5(t-2) +20.∵-5<0,∴当t=2时,h有最大值,最大值为20,故答案为2.
10.32 【点拨】设与墙垂直的一边长为xm,则与墙平行的一边长为(16-2x)m,∴矩形围栏的面积为x(16-2x)=-2x +16x= -2(x-4) +32(m ).∵-2<0,∴当x=4时,矩形围栏的最大面积为32m ,故答案为32.
11.4 【点拨】当y=3.05 时,3.05= -0.2x +x+2.25,∴x -5x+4=0,∴(x-1)(x-4)=0,解得
x =1,x =4,结合图象可知他距篮筐中心的水平距离OH是4m .故答案为4.
12.121 【点拨】当 10≤x≤20时,设y=kx+b,把点(10,20),(20,10)的坐标代入可得 解得 每天的销售量y(个)与销售价格x(元/个)的函数表达式为y=-x+30.设该食品零售店每天销售这款冷饮产品的利润为w元,w=(x-8)y=(x-8)(-x+30)=-x +38x-240=-(x-19) +121,∵ -1<0,∴当x=19时,w有最大值,最大值为121,故答案为121.
13. 【点拨】如图,以水面所在的直线AB为x轴,以过拱顶C且垂直于AB的直线为y轴建立平面直角坐标系,O为原点,由题意可得AO=OB=3米,C点坐标为(0,2),通过以上条件可设抛物线的表达式为y=ax +2,把A点坐标(-3,0)代入抛物线的表达式得,9a+2=0,解得 所以抛物线的表达式为 当x=4时,y=- 所以水面下降 米,故答案为
14.0≤w≤5;5≤w≤20 【点拨】∵物体运动的最高点离地面20米,物体从发射到落地的运动时间为3秒,∴抛物线h=-5t +mt+n的顶点的纵坐标为20,且经过点(3,0), 解 (不合题意,舍去).
∴抛物线的表达式为h=-5t +10t+ 15.∵h=-5t +10t+15= -5(t-1) +20,∴抛物线的顶点坐标为(1,20).∵20-15=5,∴当0≤t≤1时,w的取值范围是0≤w≤5.当t=2时,h=15;当t=3时,h=0.∵20-15=5,20-0=20,∴当2≤t≤3时,w的取值范围是5≤w≤20.
三、15.【解】(1)设A种品牌粽子每袋的进价是x元,B种品牌粽子每袋的进价是y元.
根据题意得 解得
答:A种品牌粽子每袋的进价是25元,B种品牌粽子每袋的进价是30元.
(2)设B品牌粽子每袋的销售价降低a元时,每天售出B品牌粽子所获得的利润最大,利润为w元.
根据题意得,w=(54-a-30)(20+5a)=-5a +100a+480=-5(a-10) +980.
∵-5<0,∴当B品牌粽子每袋的销售价降低10元时,每天售出B品牌粽子所获得的利润最大,最大利润是980 元.
16.【解】(1)根据题意,得 -2x+296,
∴y与x之间的函数表达式为y= -2x+296.
(2)根据题意,得 W=(x-34)(-2x+296)=-2(x-91) +6498.
∵-2<0,∴抛物线开口向下,W有最大值.∴当x=91时,W最大=6 498.
答:每套售价定为91元时,每天销售套件所获利润W最大,最大利润是6 498元.
17.【解】(1)∵OA=4米,且点A在y轴正半轴,∴A(0,4).
(2)∵抛物线最高点 B的坐标为(4,12),∴设抛物线的表达式为y=a(x-4) +12.
∵A(0,4)在抛物线上,∴a×(0-4) +12=4,解得
∴抛物线的函数表达式为
(3)在 Rt△CDE中, 米,∴CE=1.5米,DE=2米.∴点D的纵坐标为-1.5,
令 解得, 或
(不合题意,舍去),∴D(9.19,-1.5).∴OC≈9.19-2=7.19≈7.2(米).
∴OC的长约为7.2米.
18.【解】(1)根据表格中的数据可知,抛物线的顶点坐标为(8,23.20),∴h=8,k=23.20,
即该运动员竖直高度的最大值为23.20m,根据表格中的数据可知,
当x=0时,y=20.00,代入y=a(x-8) +23.20得20.00 = a(0-8) +23.20,解得a= -0.05,
∴函数关系式为y=-0.05(x-8) +23.20.
(2)< 【点拨】设着陆点的纵坐标为t,则第一次训练时,t= -0.05(x-8) +23.20,
解得 或
∴根据图象可知,第一次训练时着陆点的水平距离
第二次训练时,t= -0.04(x-9) +23.24,解得 或 ∴根据图象可知,第二次训练时着陆点的水平距离
易知,0<23.20-t<23.24-t,
∵20(23.20-t)<20(23.24-t)<25(23.24-t),
∴d21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 二次函数
阶段测试 二次函数的应用
一、选择题(每题4分,共32分)
1.某农机厂四月份生产零件60万个,设该厂第二季度平均每月的增长率为x,如果第二季度共生产零件y万个,那么y与x满足的函数关系式是( )
A. y=60(1+x) B. y=60+60(1+x)+60(1+x)
C. y=60(1+x)+60(1+x) D. y=60+60(1+x)
2.某旅行社在“五一”期间接团去外地旅游,经计算,所获营业额y(元)与旅行团人数x(人)满足关系式y= -x +100x+28 400,要使所获营业额最大,则此旅行团应有( )
A.30人 B.40人 C.50人 D.55人
3.已知一个直角三角形两直角边长之和为20cm,则这个直角三角形的最大面积为( )
A.25 cm B.50 cm C.100 cm D.无法确定
4.当a≤x≤a+1时,函数y=x -2x+1的最小值为1,则a的值为( )
A.-1 B.2 C.0或2 D.-1或2
5.某产品进货单价为9元,按10元一件出售时,每天能售出50件.若每件每涨价1元,每天的销售量就减少10件,则销售该产品每天能获得的最大利润为( )
A.50元 B.80元 C.90元 D.100元
6.用总长为a米的材料做成如图①所示的矩形窗框,设窗框的宽为x米,窗框的面积为y平方米,y关于x的函数图象如图②,则a的值是( )
A.16 B.12 C.8 D.4
第6题图 第7题图
7.某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的关系如图所示,D为该水流的最高点,DA⊥OB,垂足为A.已知OC = OB =8m,OA=2m,则该水流距水平面的最大高度(AD的长度)为( )
A.9m B.10m C.11m D.12m
8.九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰三角形(底边靠墙)、半圆形(如图)这三种方案,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.方案1或方案2
二、填空题(每题4分,共24分)
9.根据物理学规律,如果不考虑空气阻力,以40 m/s的速度将小球沿与地面成30°角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是 h= -5t +20t,当飞行时间为____________s时,小球达到最高点.
10.如图,用一段长为16 m的篱笆围成一个一边靠墙的矩形围栏(墙足够长),则这个围栏的最大面积为__________m .
第10题图 第11题图
11.如图,一位篮球运动员投篮,球沿抛物线y= -0.2x +x+2.25运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为3.05 m,则他距篮筐中心的水平距离OH是_____________m.
12.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当10≤x≤20时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为__________元.(利润=总销售额-总成本)
第12题图 第13题图
13.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降__________米,水面宽8米.
14.距离地面有一定高度的某发射装置竖直向上发射物体,物体离地面的高度h(米)与物体运动的时间t(秒)之间满足函数关系h= -5t +mt+n,其图象如图所示,物体运动的最高点离地面20米,物体从发射到落地的运动时间为3秒,设w表示0秒到t秒时h的值的“极差”(即0秒到t秒时h的最大值与最小值的差),则当0≤t≤1时,w的取值范围是_______________;当2≤t≤3时,w的取值范围是____________.
三、解答题(共44分)
15.(10分)端午节前夕,某超市从厂家分两次购进A,B两种品牌的粽子,两次进货时,两种品牌粽子的进价不变.第一次购进A品牌粽子100袋和B品牌粽子150袋,总费用为7000元;第二次购进A品牌粽子180袋和B品牌粽子120袋,总费用为8100 元.
(1)求A,B两种品牌粽子每袋的进价各是多少元;
(2)当B品牌粽子销售价为每袋54元时,每天可售出20袋,为了促销,该超市决定对B品牌粽子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增
加5袋.当B品牌粽子每袋的销售价降低多少元时,每天售出B品牌粽子所获得的利润最大 最大利润是多少元
16.(10分)2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为x元时,求该商品销售量y与x之间的函数表达式;
(2)求每套售价定为多少元时,每天销售套件所获利润W最大,最大利润是多少元
17.(12分)2022 北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度OA为4米,以起跳点正下方跳台底端O为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点 B的坐标为(4,12),着陆坡顶端C与落地点D的距离为2.5米,若斜坡CD的坡度i=3:4(即
求:(1)点A 的坐标;
(2)该抛物线的函数表达式;
(3)起跳点A 与着陆坡顶端C之间的水平距离OC的长.(精确到0.1米)(参考数据: 1.73)
18.(12分)单板滑雪大跳台是北京冬奥会比赛项目之一,举办场地为首钢滑雪大跳台.运动员起跳后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系,从起跳到着陆的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=a(x-h) +k(a<0).
某运动员进行了两次训练.
(1)第一次训练时,该运动员的水平距离x与竖直高度y的几组数据如下:
水平距离x/m 0 2 5 8 11 14
竖直高度y/m 20.00 21.40 22.75 23.20 22.75 21.40
根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系
(2)第二次训练时,该运动员的竖直高度y与水平距离x近似满足函数关系记该运动员第一次训练的着陆点的水平距离为 d ,第二次训练的着陆点的水平距离为d ,则 d _______d .(填“>”“=”或“<”)
参考答案
一、1. B 【点拨】该农机厂五月份生产零件( x)万个,六月份生产零件60(1+x) 万个.∵第二季度包括四月份、五月份和六月份,∴由“第二季度共生产零件y万个”可得y=60+60(1+x)+60(1+x) .
2. C 【点拨】y=-x +100x+28 400=-(x-50) +30900,当x=50时, 故选 C.
3. B 【点拨】设一条直角边为xcm,则另一条直角边为 50(cm ). ∴当x=10 时, 故选B.
4. D 【点拨】当y=1时,有x -2x+1=1,解得x =0,x =2.∵当a≤x≤a+1时,函数有最小值1,∴a=2或a+1=0,如图所示.∴a=2或a=-1,故选D.
5. C 【点拨】设销售单价定为x元,总利润为W元,则可得销量为[50-10(x-10)]件,单件利润为(x-9)元,由题意得,W=(x-9)[50-10(x-10)]=-10x +240x-1 350= -10(x-12) +90,故可得当x=12时,W取得最大值,为90.故选C.
6. B 【点拨】由图象可知,当x=2时,y有最大值,最大值为4,∴当x=2时,窗框的最大面积是4平方米,根据矩形面积计算公式,另一边为4÷2=2(米),∴材料总长为3×2+3×2=12(米).故选B.
7. A【点拨】根据题意,设抛物线的表达式为 y=a(x-2) +k,将点C(0,8)、B(8,0)的坐标代入,得 解得 抛物线的表达式为 .当x=2时,y=9,即AD=9m,故选A.
8. C 【点拨】如图,方案1:设AD=x米,则AB=(8-2x)米,则菜园面积为x(8-2x)=-2x +8x=-2·
(x-2) +8((平方米),当x=2时,此时菜园最大面积为8平方米.方案2:当∠BAC=90°时,菜园最大面积为 (平方米).方案3:易得半圆形的半径为米,此时菜园面积为 (平方米). .最佳方案是方案3.
二、9.2 【点拨】h=-5t +20t= -5(t-2) +20.∵-5<0,∴当t=2时,h有最大值,最大值为20,故答案为2.
10.32 【点拨】设与墙垂直的一边长为xm,则与墙平行的一边长为(16-2x)m,∴矩形围栏的面积为x(16-2x)=-2x +16x= -2(x-4) +32(m ).∵-2<0,∴当x=4时,矩形围栏的最大面积为32m ,故答案为32.
11.4 【点拨】当y=3.05 时,3.05= -0.2x +x+2.25,∴x -5x+4=0,∴(x-1)(x-4)=0,解得
x =1,x =4,结合图象可知他距篮筐中心的水平距离OH是4m .故答案为4.
12.121 【点拨】当 10≤x≤20时,设y=kx+b,把点(10,20),(20,10)的坐标代入可得 解得 每天的销售量y(个)与销售价格x(元/个)的函数表达式为y=-x+30.设该食品零售店每天销售这款冷饮产品的利润为w元,w=(x-8)y=(x-8)(-x+30)=-x +38x-240=-(x-19) +121,∵ -1<0,∴当x=19时,w有最大值,最大值为121,故答案为121.
13. 【点拨】如图,以水面所在的直线AB为x轴,以过拱顶C且垂直于AB的直线为y轴建立平面直角坐标系,O为原点,由题意可得AO=OB=3米,C点坐标为(0,2),通过以上条件可设抛物线的表达式为y=ax +2,把A点坐标(-3,0)代入抛物线的表达式得,9a+2=0,解得 所以抛物线的表达式为 当x=4时,y=- 所以水面下降 米,故答案为
14.0≤w≤5;5≤w≤20 【点拨】∵物体运动的最高点离地面20米,物体从发射到落地的运动时间为3秒,∴抛物线h=-5t +mt+n的顶点的纵坐标为20,且经过点(3,0), 解 (不合题意,舍去).
∴抛物线的表达式为h=-5t +10t+ 15.∵h=-5t +10t+15= -5(t-1) +20,∴抛物线的顶点坐标为(1,20).∵20-15=5,∴当0≤t≤1时,w的取值范围是0≤w≤5.当t=2时,h=15;当t=3时,h=0.∵20-15=5,20-0=20,∴当2≤t≤3时,w的取值范围是5≤w≤20.
三、15.【解】(1)设A种品牌粽子每袋的进价是x元,B种品牌粽子每袋的进价是y元.
根据题意得 解得
答:A种品牌粽子每袋的进价是25元,B种品牌粽子每袋的进价是30元.
(2)设B品牌粽子每袋的销售价降低a元时,每天售出B品牌粽子所获得的利润最大,利润为w元.
根据题意得,w=(54-a-30)(20+5a)=-5a +100a+480=-5(a-10) +980.
∵-5<0,∴当B品牌粽子每袋的销售价降低10元时,每天售出B品牌粽子所获得的利润最大,最大利润是980 元.
16.【解】(1)根据题意,得 -2x+296,
∴y与x之间的函数表达式为y= -2x+296.
(2)根据题意,得 W=(x-34)(-2x+296)=-2(x-91) +6498.
∵-2<0,∴抛物线开口向下,W有最大值.∴当x=91时,W最大=6 498.
答:每套售价定为91元时,每天销售套件所获利润W最大,最大利润是6 498元.
17.【解】(1)∵OA=4米,且点A在y轴正半轴,∴A(0,4).
(2)∵抛物线最高点 B的坐标为(4,12),∴设抛物线的表达式为y=a(x-4) +12.
∵A(0,4)在抛物线上,∴a×(0-4) +12=4,解得
∴抛物线的函数表达式为
(3)在 Rt△CDE中, 米,∴CE=1.5米,DE=2米.∴点D的纵坐标为-1.5,
令 解得, 或
(不合题意,舍去),∴D(9.19,-1.5).∴OC≈9.19-2=7.19≈7.2(米).
∴OC的长约为7.2米.
18.【解】(1)根据表格中的数据可知,抛物线的顶点坐标为(8,23.20),∴h=8,k=23.20,
即该运动员竖直高度的最大值为23.20m,根据表格中的数据可知,
当x=0时,y=20.00,代入y=a(x-8) +23.20得20.00 = a(0-8) +23.20,解得a= -0.05,
∴函数关系式为y=-0.05(x-8) +23.20.
(2)< 【点拨】设着陆点的纵坐标为t,则第一次训练时,t= -0.05(x-8) +23.20,
解得 或
∴根据图象可知,第一次训练时着陆点的水平距离
第二次训练时,t= -0.04(x-9) +23.24,解得 或 ∴根据图象可知,第二次训练时着陆点的水平距离
易知,0<23.20-t<23.24-t,
∵20(23.20-t)<20(23.24-t)<25(23.24-t),
∴d
21世纪教育网(www.21cnjy.com)
