3.5.1 确定含有两个待定字母的二次函数表达式同步练习(含答案)
文档属性
| 名称 | 3.5.1 确定含有两个待定字母的二次函数表达式同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 935.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 20:26:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第三章 二次函数
5 确定二次函数的表达式
第1课时 确定含有两个待定字母的二次函数表达式
认知基础练
练点1 已知均不为顶点的两点坐标求二次函数表达式
1.已知二次函数y=ax +bx-6的图象经过点A(1,-3),B(-1,-3),则二次函数的表达式为( )
A. y=3x -6 B. y=x +2x-6 C. y=9x +6x-6 D. y=9x -6x-6
2.若二次函数y=ax +bx-(a+b)图象经过A(-1,4),B(0,-1)两个点,则该二次函数的表达式为_______________.
练点2 已知顶点和另一点坐标求二次函数表达式
3.一个二次函数图象的顶点坐标是(2,4),且过点(0,-4),则这个二次函数的表达式为( )
A. y= -2(x+2) +4 B. y=2(x+2) -4 C. y= -2(x-2) +4 D. y=2(x-2) -4
4.若抛物线y=a(x-h) +k的顶点为A(1,-1),且经过点A关于原点O的对称点 ,则抛物线的表达式为( )
5.小聪在画一个二次函数的图象时,列出了下面几组y与x的对应值:
x … 0 1 2 3 4 5 …
y … 5 0 -3 -4 -3 0 …
该二次函数的表达式为____________.
纠易错 将点的坐标代错式子而致错
6.二次函数y=2x +bx+c的图象经过点(2,3),且顶点在直线y=3x-2上,则二次函数
的表达式为____________.
思维发散练
发散点1 利用两点坐标求函数表达式的应用
7.如图,抛物线 y=ax +bx-4(a≠0)与x轴交于点 A(1,0),B(-2,0),与y轴交于点 C.
(1)求抛物线的表达式,并写出顶点 D的坐标;
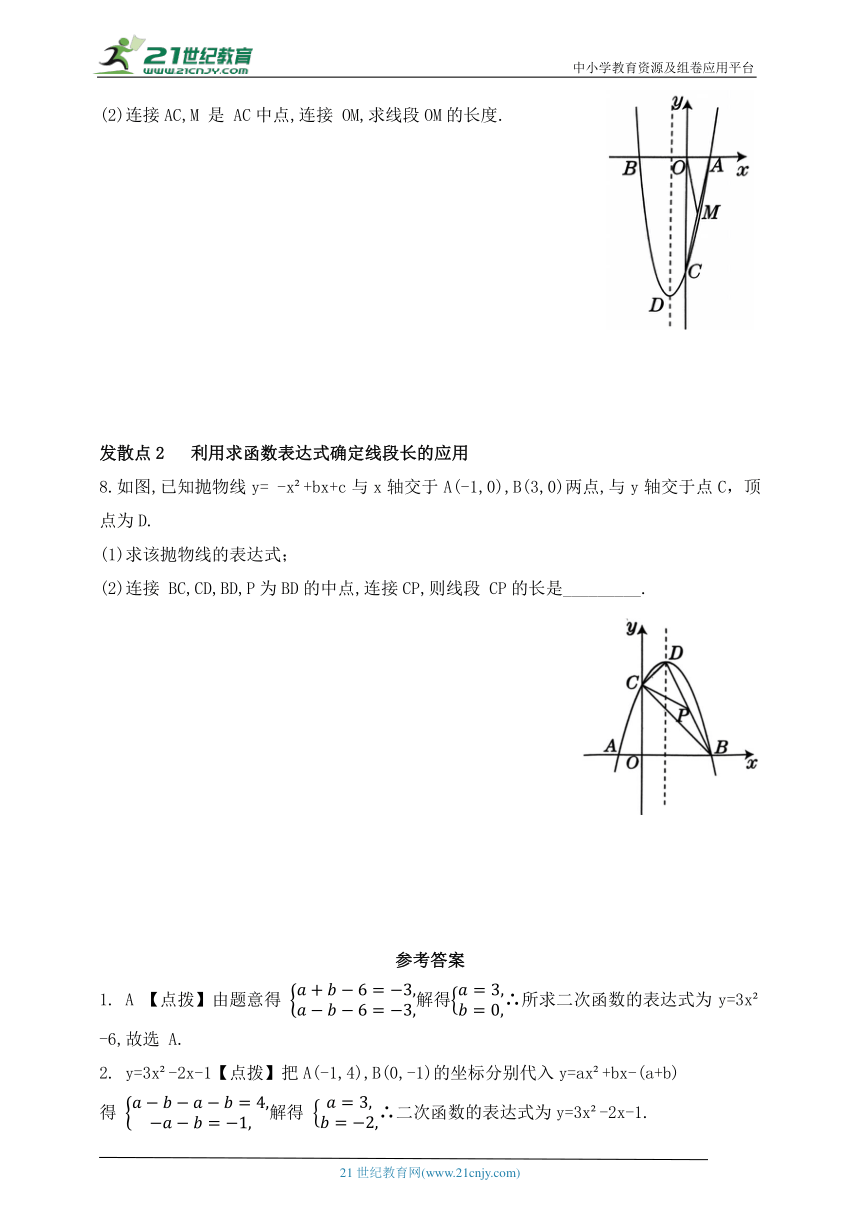
(2)连接AC,M 是 AC中点,连接 OM,求线段OM的长度.
发散点2 利用求函数表达式确定线段长的应用
8.如图,已知抛物线y= -x +bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,顶点为D.
(1)求该抛物线的表达式;
(2)连接 BC,CD,BD,P为BD的中点,连接CP,则线段 CP的长是_________.
参考答案
1. A 【点拨】由题意得 解得∴所求二次函数的表达式为y=3x -6,故选 A.
2. y=3x -2x-1【点拨】把A(-1,4),B(0,-1)的坐标分别代入y=ax +bx-(a+b)
得 解得 ∴二次函数的表达式为y=3x -2x-1.
3. C 【点拨】设所求二次函数的表达式为y=a(x-2) +4,则a(0-2) +4= -4,
∴a= -2,∴所求二次函数的表达式为y=-2(x-2) +4,故选C.
4. D【点拨】∵抛物线y=a(x-h) +k的顶点为A(1,-1),∴y=a(x-1) -1.
∵抛物线经过点A关于原点O的对称点 解得a=
抛物线的表达式为 故选D.
5. y=(x-3) -4(或y=x -6x+5)【点拨】由表格数据结合二次函数图象的对称性可得图象顶点为(3,-4),设二次函数的表达式为y=a(x-3) -4(a≠0),将点(1,0)的坐标代入得4a-4=0,解得a=1,∴该二次函数的表达式为y=(x-3) -4((或y=x -6x+5).
6. y=2x -4x+3或y=2x -6x+7
【点拨】 ∴图象的顶点 坐标为 将点 的坐标代入y=3x-2,得 即b -6b- 16 -8c= 0①,将点(2,3)的坐标代入y=2x +bx+c,得3=8+2b+c,即c= -5-2b②,
将②代入①,得b -6b-16-8(-5-2b)=0,解得b =-4,b =-6.
当b= -4时,c=3,当b= -6时,c=7.
∴二次函数的表达式为y=2x -4x+3或y=2x -6x+7.
点易错 本题易出现顶点坐标与已知点的坐标混用导致出错的现象.
7.【解】(1)把A(1,0),B(-2,0)的坐标代入y=ax +bx-4得 解得
∴抛物线的表达式为y=2x +2x-4,顶点D的坐标为
(2)∵抛物线的表达式为y=2x +2x-4,∴当x=0时,y= -4,∴C的坐标为(0,-4),
∴M的坐标为
8.【解】(1)(方法一)∵抛物线y=-x +bx+c与x轴交于A(-1,0),B(3,0)两点,
解得 ∴该抛物线的表达式为y= -x +2x+3.
(方法二)∵抛物线y=-x +bx+c与x轴交于A(-1,0),B(3,0)两点,
∴ 抛物线的表达式为y=-(x+1)(x-3),即y= -x +2x+3.
【点拨】∵y= -x +2x+3=-(x-1) +4,∴D(1,4),把x=0代入y= -x +2x+3,得y=3,
∴C(0,3).∵P为BD的中点,∴P(2,2), 故答案为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 二次函数
5 确定二次函数的表达式
第1课时 确定含有两个待定字母的二次函数表达式
认知基础练
练点1 已知均不为顶点的两点坐标求二次函数表达式
1.已知二次函数y=ax +bx-6的图象经过点A(1,-3),B(-1,-3),则二次函数的表达式为( )
A. y=3x -6 B. y=x +2x-6 C. y=9x +6x-6 D. y=9x -6x-6
2.若二次函数y=ax +bx-(a+b)图象经过A(-1,4),B(0,-1)两个点,则该二次函数的表达式为_______________.
练点2 已知顶点和另一点坐标求二次函数表达式
3.一个二次函数图象的顶点坐标是(2,4),且过点(0,-4),则这个二次函数的表达式为( )
A. y= -2(x+2) +4 B. y=2(x+2) -4 C. y= -2(x-2) +4 D. y=2(x-2) -4
4.若抛物线y=a(x-h) +k的顶点为A(1,-1),且经过点A关于原点O的对称点 ,则抛物线的表达式为( )
5.小聪在画一个二次函数的图象时,列出了下面几组y与x的对应值:
x … 0 1 2 3 4 5 …
y … 5 0 -3 -4 -3 0 …
该二次函数的表达式为____________.
纠易错 将点的坐标代错式子而致错
6.二次函数y=2x +bx+c的图象经过点(2,3),且顶点在直线y=3x-2上,则二次函数
的表达式为____________.
思维发散练
发散点1 利用两点坐标求函数表达式的应用
7.如图,抛物线 y=ax +bx-4(a≠0)与x轴交于点 A(1,0),B(-2,0),与y轴交于点 C.
(1)求抛物线的表达式,并写出顶点 D的坐标;
(2)连接AC,M 是 AC中点,连接 OM,求线段OM的长度.
发散点2 利用求函数表达式确定线段长的应用
8.如图,已知抛物线y= -x +bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,顶点为D.
(1)求该抛物线的表达式;
(2)连接 BC,CD,BD,P为BD的中点,连接CP,则线段 CP的长是_________.
参考答案
1. A 【点拨】由题意得 解得∴所求二次函数的表达式为y=3x -6,故选 A.
2. y=3x -2x-1【点拨】把A(-1,4),B(0,-1)的坐标分别代入y=ax +bx-(a+b)
得 解得 ∴二次函数的表达式为y=3x -2x-1.
3. C 【点拨】设所求二次函数的表达式为y=a(x-2) +4,则a(0-2) +4= -4,
∴a= -2,∴所求二次函数的表达式为y=-2(x-2) +4,故选C.
4. D【点拨】∵抛物线y=a(x-h) +k的顶点为A(1,-1),∴y=a(x-1) -1.
∵抛物线经过点A关于原点O的对称点 解得a=
抛物线的表达式为 故选D.
5. y=(x-3) -4(或y=x -6x+5)【点拨】由表格数据结合二次函数图象的对称性可得图象顶点为(3,-4),设二次函数的表达式为y=a(x-3) -4(a≠0),将点(1,0)的坐标代入得4a-4=0,解得a=1,∴该二次函数的表达式为y=(x-3) -4((或y=x -6x+5).
6. y=2x -4x+3或y=2x -6x+7
【点拨】 ∴图象的顶点 坐标为 将点 的坐标代入y=3x-2,得 即b -6b- 16 -8c= 0①,将点(2,3)的坐标代入y=2x +bx+c,得3=8+2b+c,即c= -5-2b②,
将②代入①,得b -6b-16-8(-5-2b)=0,解得b =-4,b =-6.
当b= -4时,c=3,当b= -6时,c=7.
∴二次函数的表达式为y=2x -4x+3或y=2x -6x+7.
点易错 本题易出现顶点坐标与已知点的坐标混用导致出错的现象.
7.【解】(1)把A(1,0),B(-2,0)的坐标代入y=ax +bx-4得 解得
∴抛物线的表达式为y=2x +2x-4,顶点D的坐标为
(2)∵抛物线的表达式为y=2x +2x-4,∴当x=0时,y= -4,∴C的坐标为(0,-4),
∴M的坐标为
8.【解】(1)(方法一)∵抛物线y=-x +bx+c与x轴交于A(-1,0),B(3,0)两点,
解得 ∴该抛物线的表达式为y= -x +2x+3.
(方法二)∵抛物线y=-x +bx+c与x轴交于A(-1,0),B(3,0)两点,
∴ 抛物线的表达式为y=-(x+1)(x-3),即y= -x +2x+3.
【点拨】∵y= -x +2x+3=-(x-1) +4,∴D(1,4),把x=0代入y= -x +2x+3,得y=3,
∴C(0,3).∵P为BD的中点,∴P(2,2), 故答案为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
