第三章 二次函数 专题 二次函数的图象与性质的应用的九种常见类型(含答案)
文档属性
| 名称 | 第三章 二次函数 专题 二次函数的图象与性质的应用的九种常见类型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 20:28:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章 二次函数
专题 二次函数的图象与性质的应用的九种常见类型
类型1 二次函数的图象在解题中的应用
1.一次函数y=ax+b的图象如图所示,则二次函数y=ax +bx的图象可能是( )
2.如图,四边形 OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点 B在抛物线y=ax (a<0)上,则a=( )
A.-2
类型2 二次函数的性质在解题中的应用(分类讨论思想)
3.在平面直角坐标系中,抛物线y=x +2mx+2m -m的顶点为A.
(1)求顶点A 的坐标;(用含有字母m的代数式表示)
(2)若点B(2,yB),C(5, yc)在抛物线上,且 ,则m的取值范围是__________;
(3)当1≤x≤3时,函数的最小值等于6,求m的值.
类型3 二次函数图象的平移在解题中的应用
4.把抛物线C :y=x +2x+3先向右平移4个单位,再向下平移5个单位得到抛物线 C .
(1)直接写出抛物线 C 的函数表达式.
(2)动点P(a,-6)能否在抛物线 C 上 请说明理由.
(3)若点A(m,y ),B(n,y )都在抛物线 C 上,且m类型4 二次函数图象上的点的坐标在解题中的应用
5.如图,点 P(a,3)在抛物线 C:y=4-(6-x) 上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为P',C'.平移该胶片,使( 所在抛物线对应的函数恰为y= -x +6x- 9.求点 移动的最短路程.
类型5 二次函数图象与坐标轴的交点在解题中的应用
6.抛物线 与x轴正半轴交于点A,与y轴交于点 B.
(1)求直线AB的表达式及抛物线顶点坐标;
(2)如图①,点P为第四象限内、抛物线对称轴右侧部分上一动点,过点 P作PC⊥x轴,垂足为C,PC 交AB于点 D,求 PD+BD的最大值,并求出此时点P的坐标;
(3)如图②,将抛物线 向右平移得到抛物线 直线AB 与抛物线 交于M,N两点,若点A是线段MN的中点,求抛物线. 的表达式.
类型6 二次函数图象与直线的交点在解题中的应用
7.如图,抛物线y=-x +bx+c过点A(-1,0),B(3,0),与y轴交于点 C.
(1)求抛物线的表达式.
(2)点P为抛物线对称轴上一动点,当△PCB是以BC 为底边的等腰三角形时,求点P的坐标.
(3)在(2)的条件下,是否存在点 M为抛物线第一象限上的点,使得 若存在,求出点 M的横坐标;若不存在,请说明理由.
类型7 二次函数最值在解题中的应用
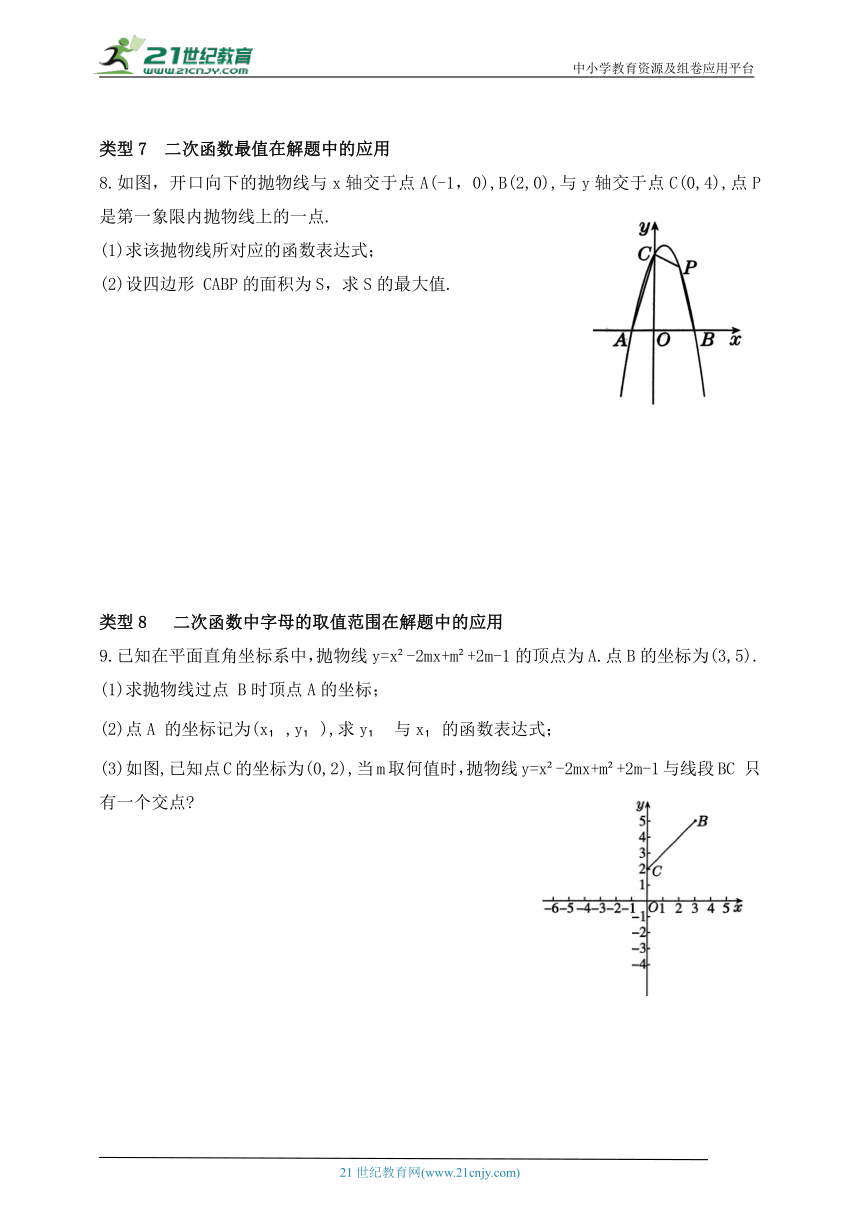
8.如图,开口向下的抛物线与x轴交于点A(-1,0),B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数表达式;
(2)设四边形 CABP的面积为S,求S的最大值.
类型8 二次函数中字母的取值范围在解题中的应用
9.已知在平面直角坐标系中,抛物线y=x -2mx+m +2m-1的顶点为A.点B的坐标为(3,5).
(1)求抛物线过点 B时顶点A的坐标;
(2)点A 的坐标记为(x ,y ),求y 与x 的函数表达式;
(3)如图,已知点C的坐标为(0,2),当m取何值时,抛物线y=x -2mx+m +2m-1与线段BC 只有一个交点
类型9 二次函数图象与四边形的综合在解题中的应用
10.【开放与探究】如图①,抛物线y=ax +2x+c,交x轴于A,B两点,交y轴于点 C,F为抛物线顶点,直线 EF垂直于x轴于点E,当y≥0时,-1≤x≤3.
(1)求抛物线的表达式;
(2)点P 是线段 BE 上的动点(除B,E 外),过点P作x轴的垂线交抛物线于点 D.
①当点 P 的横坐标为2时,求四边形 ACFD的面积;
②如图②,直线AD,BD分别与抛物线对称轴交于M,N两点.试问,EM+EN是否为定值 如果是,请求出这个定值;如果不是,请说明理由.
参考答案
1. D【点拨】由一次函数y=ax+b的图象可知,抛物线y=ax +bx的开口向下,对称轴在y轴的右侧,故选D.
2. C 【点拨】连接OB.∵四边形OABC 是边长为1的正方形, 过点B作 BD⊥x轴于D.∵OC与x轴正半轴的夹角为15°,∴∠BOD=.点B的坐标为 ∵点B在抛物线y=ax (a<0)上,∴ 解得 故选C.
3.【解】(1)y=x +2mx+2m -m=(x+m) +m -m,∴顶点A的坐标为(-m,m -m).
(3)由(1)知抛物线的对称轴为直线x=-m.
①若-m<1,则m>-1,当1≤x≤3时,y随x的增大而增大,
∴当x=1时,y取得最小值,最小值为1 +2m+2m -m=2m +m+1.
又∵函数的最小值等于6,∴2m +m+1=6,解得 (舍去);
②若-m>3,则m<-3,当1≤x≤3时,y随x的增大而减小,
∴当x=3时,y取得最小值,最小值为3 +2m×3+2m -m=2m +5m+9.
又∵函数的最小值等于6,∴2m +5m+9=6,解得 (舍去),m = -1(舍去);
③若1≤-m≤3,则-3≤m≤-1,当x=-m时,y取得最小值,最小值为m -m.
又∵函数的最小值等于6,∴m -m=6,解得m =3((舍去),m =-2.
综上所述,m的值为 或-2.
4.【解】(1)抛物线C 的函数表达式为y=(x-3) -3.
(2)动点 P(a,-6)不能在抛物线 C 上.理由如下:
∵抛物线C 的函数表达式为y=(x-3) -3,∴函数的最小值为-3.
∵-6<-3,∴动点P(a,-6)不能在抛物线 C 上.
(3)y >y .理由如下:∵抛物线C 的函数表达式为y=(x-3) -3,
∴抛物线的开口向上,对称轴为直线x=3.∴当x<3时,y随x的增大而减小.
∵点A(m,y ),B(n,y )都在抛物线 C 上,且my .
5.【解】(1)∵抛物线C:y=4-(6-x) =-(x-6) +4,∴抛物线的顶点为(6,4),∴抛物线的对称轴为直线x=6,y的最大值为4,当y=3时,3=-(x-6) +4,解得x =5,x =7.
∵点P(a,3)在对称轴的右侧,∴a>6,∴a=7.
(2)∵平移后的抛物线的表达式为y=-(x-3) ,∴平移后的顶点为(3,0).
∵平移前抛物线的顶点为(6,4),∴点 P'移动的最短路程为
6.【解】(1)对于 令y=0,则解得: 令x=0,则y= -3,∴B(0,-3).
设直线AB的表达式为y=kx+b,
将A(4,0),B(0,-3)的坐标分别代入,得 解得
∴直线AB的表达式为
∴抛物线顶点坐标为
(2)∵A(4,0),B(0,-3),∴OA=4,OB=3.
又∵
∵点P在抛物线上,∴设
∵PC⊥x轴,∴点 D的横坐标为n.
又∵点D在直线AB上,∴
易知
由(1)知抛物线的对称轴为直线 由题意可得 又∵
∴当 时,PD+BD有最大值,最大值为 此时 点P的坐标为
(3)设抛物线 的表达式为
可得
设M(x ,y ),N(x ,y ).∴x ,x 是方程 的两根.
∵点A(4,0)是线段 MN的中点, 解得
∴抛物线L'的表达式为 即
7.【解】(1)由题意得y=-(x+1)(x-3),∴y= -x +2x+3.
(2)由(1)可得该抛物线的对称轴为直线x=1.
令x=0,则y=3,∴C(0,3).设P(1,m).
∵PB=PC,∴PB =PC .∴(3-1) +m =1 +(3-m) ,解得m=1.∴P(1,1).
(3)存在.
假设存在点M满足条件,作PQ∥BC交y轴于点Q,作MN∥BC交y轴于点 N.
设直线 BC 的表达式为y=kx+a,将点 B(3,0)、点C(0,3)的坐标分别代入,
得 解得 直线BC的表达式为
又∵P(1,1),∴直线PQ的表达式为y= -x+2.
∴Q(0,2).∵C(0,3),S△BCM=S△BCp,∴N(0,4).∴直线 MN的表达式为y=-x+4.
由题意得-x +2x+3= -x+4,解得 ∴点M的横坐标为 或
8.【解】(1)由题意可设抛物线所对应的函数表达式为y=a(x+1)(x-2).
将C(0,4)的坐标代入,得4= -2a,解得a=-2,
∴该抛物线所对应的函数表达式为y= -2(x+1)·(x-2),即y= -2x +2x+4.
(2)如图,连接OP,设点P的坐标为(m,-2m +2m+4),由题意可知0∵A(-1,0),B(2,0),C(0,4),∴OA=1,OB=2,OC=4.
-2m +4m+6= -2(m-1) +8.∵-2<0,∴当m=1时,S最大,最大值为8.
9.【解】(1)∵抛物线y=x -2mx+m +2m-1过点B(3,5),
∴9-6m+m +2m-1=5,解得m =1,m =3.
当m=1时,y=x -2x+2=(x-1) +1,此时抛物线的顶点A的坐标为(1,1);
当m=3时,y=x -6x+14=(x-3) +5,此时抛物线的顶点A 的坐标为(3,5).
综上,抛物线过点 B时顶点A 的坐标为(1,1)或(3,5).
(2)∵y=x -2mx+m +2m-1=(x-m) +2m-1,∴顶点A 的坐标为(m,2m-1).
又∵点A的坐标记为(x ,y ),∴x =m,y =2m-1.
∴y 与x 的函数表达式为y =2x -1.
(3)由(2)可知,抛物线的顶点A 在直线y=2x-1上.
由(1)知,当m=1或m=3时,抛物线过点 B(3,5).
把C(0,2)的坐标代入y=x -2mx+m +2m-1,得m +2m-1=2,解得m =1,m = -3.
∴当m=1或-3时,抛物线经过点C(0,2).
如图,当m= -3或m=3时,抛物线与线段 BC只有一个交点;
当m=1时,抛物线同时过点 B,C,不合题意.
∴当-3≤m≤3且m≠1时,抛物线y=x -2mx+m +2m-1与线段BC只有一个交点.
10.【解】(1)∵当y≥0时,-1≤x≤3,
∴x =-1,x =3是方程ax +2x+c=0的两根,A(-1,0),B(3,0),
解得 ∴抛物线的表达式为y=-x +2x+3.
(2)①连接 CD. 把x=2代入y=-x +2x+3得y=3,∴D(2,3).又当x=0时,y=3,∴C(0,3),
∴线段 CD∥x轴.∴CD=2.
∵y= -x +2x+3=-(x-1) +4,
②EM+EN为定值.设D(m,-m +2m+3)(1设直线AD的表达式为y=k x+b ,BD的表达式为y=k x+b ,
由题意可得
解得
∴直线AD的表达式为 y=(3-m)x+(3-m),直线BD的表达式为y= -(m+1)x+3(m+1).
令x=1,得 ∴ME=6-2m,NE=2m+2,∴NE+ME =8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 二次函数
专题 二次函数的图象与性质的应用的九种常见类型
类型1 二次函数的图象在解题中的应用
1.一次函数y=ax+b的图象如图所示,则二次函数y=ax +bx的图象可能是( )
2.如图,四边形 OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点 B在抛物线y=ax (a<0)上,则a=( )
A.-2
类型2 二次函数的性质在解题中的应用(分类讨论思想)
3.在平面直角坐标系中,抛物线y=x +2mx+2m -m的顶点为A.
(1)求顶点A 的坐标;(用含有字母m的代数式表示)
(2)若点B(2,yB),C(5, yc)在抛物线上,且 ,则m的取值范围是__________;
(3)当1≤x≤3时,函数的最小值等于6,求m的值.
类型3 二次函数图象的平移在解题中的应用
4.把抛物线C :y=x +2x+3先向右平移4个单位,再向下平移5个单位得到抛物线 C .
(1)直接写出抛物线 C 的函数表达式.
(2)动点P(a,-6)能否在抛物线 C 上 请说明理由.
(3)若点A(m,y ),B(n,y )都在抛物线 C 上,且m
5.如图,点 P(a,3)在抛物线 C:y=4-(6-x) 上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为P',C'.平移该胶片,使( 所在抛物线对应的函数恰为y= -x +6x- 9.求点 移动的最短路程.
类型5 二次函数图象与坐标轴的交点在解题中的应用
6.抛物线 与x轴正半轴交于点A,与y轴交于点 B.
(1)求直线AB的表达式及抛物线顶点坐标;
(2)如图①,点P为第四象限内、抛物线对称轴右侧部分上一动点,过点 P作PC⊥x轴,垂足为C,PC 交AB于点 D,求 PD+BD的最大值,并求出此时点P的坐标;
(3)如图②,将抛物线 向右平移得到抛物线 直线AB 与抛物线 交于M,N两点,若点A是线段MN的中点,求抛物线. 的表达式.
类型6 二次函数图象与直线的交点在解题中的应用
7.如图,抛物线y=-x +bx+c过点A(-1,0),B(3,0),与y轴交于点 C.
(1)求抛物线的表达式.
(2)点P为抛物线对称轴上一动点,当△PCB是以BC 为底边的等腰三角形时,求点P的坐标.
(3)在(2)的条件下,是否存在点 M为抛物线第一象限上的点,使得 若存在,求出点 M的横坐标;若不存在,请说明理由.
类型7 二次函数最值在解题中的应用
8.如图,开口向下的抛物线与x轴交于点A(-1,0),B(2,0),与y轴交于点C(0,4),点P是第一象限内抛物线上的一点.
(1)求该抛物线所对应的函数表达式;
(2)设四边形 CABP的面积为S,求S的最大值.
类型8 二次函数中字母的取值范围在解题中的应用
9.已知在平面直角坐标系中,抛物线y=x -2mx+m +2m-1的顶点为A.点B的坐标为(3,5).
(1)求抛物线过点 B时顶点A的坐标;
(2)点A 的坐标记为(x ,y ),求y 与x 的函数表达式;
(3)如图,已知点C的坐标为(0,2),当m取何值时,抛物线y=x -2mx+m +2m-1与线段BC 只有一个交点
类型9 二次函数图象与四边形的综合在解题中的应用
10.【开放与探究】如图①,抛物线y=ax +2x+c,交x轴于A,B两点,交y轴于点 C,F为抛物线顶点,直线 EF垂直于x轴于点E,当y≥0时,-1≤x≤3.
(1)求抛物线的表达式;
(2)点P 是线段 BE 上的动点(除B,E 外),过点P作x轴的垂线交抛物线于点 D.
①当点 P 的横坐标为2时,求四边形 ACFD的面积;
②如图②,直线AD,BD分别与抛物线对称轴交于M,N两点.试问,EM+EN是否为定值 如果是,请求出这个定值;如果不是,请说明理由.
参考答案
1. D【点拨】由一次函数y=ax+b的图象可知,抛物线y=ax +bx的开口向下,对称轴在y轴的右侧,故选D.
2. C 【点拨】连接OB.∵四边形OABC 是边长为1的正方形, 过点B作 BD⊥x轴于D.∵OC与x轴正半轴的夹角为15°,∴∠BOD=.点B的坐标为 ∵点B在抛物线y=ax (a<0)上,∴ 解得 故选C.
3.【解】(1)y=x +2mx+2m -m=(x+m) +m -m,∴顶点A的坐标为(-m,m -m).
(3)由(1)知抛物线的对称轴为直线x=-m.
①若-m<1,则m>-1,当1≤x≤3时,y随x的增大而增大,
∴当x=1时,y取得最小值,最小值为1 +2m+2m -m=2m +m+1.
又∵函数的最小值等于6,∴2m +m+1=6,解得 (舍去);
②若-m>3,则m<-3,当1≤x≤3时,y随x的增大而减小,
∴当x=3时,y取得最小值,最小值为3 +2m×3+2m -m=2m +5m+9.
又∵函数的最小值等于6,∴2m +5m+9=6,解得 (舍去),m = -1(舍去);
③若1≤-m≤3,则-3≤m≤-1,当x=-m时,y取得最小值,最小值为m -m.
又∵函数的最小值等于6,∴m -m=6,解得m =3((舍去),m =-2.
综上所述,m的值为 或-2.
4.【解】(1)抛物线C 的函数表达式为y=(x-3) -3.
(2)动点 P(a,-6)不能在抛物线 C 上.理由如下:
∵抛物线C 的函数表达式为y=(x-3) -3,∴函数的最小值为-3.
∵-6<-3,∴动点P(a,-6)不能在抛物线 C 上.
(3)y >y .理由如下:∵抛物线C 的函数表达式为y=(x-3) -3,
∴抛物线的开口向上,对称轴为直线x=3.∴当x<3时,y随x的增大而减小.
∵点A(m,y ),B(n,y )都在抛物线 C 上,且m
5.【解】(1)∵抛物线C:y=4-(6-x) =-(x-6) +4,∴抛物线的顶点为(6,4),∴抛物线的对称轴为直线x=6,y的最大值为4,当y=3时,3=-(x-6) +4,解得x =5,x =7.
∵点P(a,3)在对称轴的右侧,∴a>6,∴a=7.
(2)∵平移后的抛物线的表达式为y=-(x-3) ,∴平移后的顶点为(3,0).
∵平移前抛物线的顶点为(6,4),∴点 P'移动的最短路程为
6.【解】(1)对于 令y=0,则解得: 令x=0,则y= -3,∴B(0,-3).
设直线AB的表达式为y=kx+b,
将A(4,0),B(0,-3)的坐标分别代入,得 解得
∴直线AB的表达式为
∴抛物线顶点坐标为
(2)∵A(4,0),B(0,-3),∴OA=4,OB=3.
又∵
∵点P在抛物线上,∴设
∵PC⊥x轴,∴点 D的横坐标为n.
又∵点D在直线AB上,∴
易知
由(1)知抛物线的对称轴为直线 由题意可得 又∵
∴当 时,PD+BD有最大值,最大值为 此时 点P的坐标为
(3)设抛物线 的表达式为
可得
设M(x ,y ),N(x ,y ).∴x ,x 是方程 的两根.
∵点A(4,0)是线段 MN的中点, 解得
∴抛物线L'的表达式为 即
7.【解】(1)由题意得y=-(x+1)(x-3),∴y= -x +2x+3.
(2)由(1)可得该抛物线的对称轴为直线x=1.
令x=0,则y=3,∴C(0,3).设P(1,m).
∵PB=PC,∴PB =PC .∴(3-1) +m =1 +(3-m) ,解得m=1.∴P(1,1).
(3)存在.
假设存在点M满足条件,作PQ∥BC交y轴于点Q,作MN∥BC交y轴于点 N.
设直线 BC 的表达式为y=kx+a,将点 B(3,0)、点C(0,3)的坐标分别代入,
得 解得 直线BC的表达式为
又∵P(1,1),∴直线PQ的表达式为y= -x+2.
∴Q(0,2).∵C(0,3),S△BCM=S△BCp,∴N(0,4).∴直线 MN的表达式为y=-x+4.
由题意得-x +2x+3= -x+4,解得 ∴点M的横坐标为 或
8.【解】(1)由题意可设抛物线所对应的函数表达式为y=a(x+1)(x-2).
将C(0,4)的坐标代入,得4= -2a,解得a=-2,
∴该抛物线所对应的函数表达式为y= -2(x+1)·(x-2),即y= -2x +2x+4.
(2)如图,连接OP,设点P的坐标为(m,-2m +2m+4),由题意可知0
-2m +4m+6= -2(m-1) +8.∵-2<0,∴当m=1时,S最大,最大值为8.
9.【解】(1)∵抛物线y=x -2mx+m +2m-1过点B(3,5),
∴9-6m+m +2m-1=5,解得m =1,m =3.
当m=1时,y=x -2x+2=(x-1) +1,此时抛物线的顶点A的坐标为(1,1);
当m=3时,y=x -6x+14=(x-3) +5,此时抛物线的顶点A 的坐标为(3,5).
综上,抛物线过点 B时顶点A 的坐标为(1,1)或(3,5).
(2)∵y=x -2mx+m +2m-1=(x-m) +2m-1,∴顶点A 的坐标为(m,2m-1).
又∵点A的坐标记为(x ,y ),∴x =m,y =2m-1.
∴y 与x 的函数表达式为y =2x -1.
(3)由(2)可知,抛物线的顶点A 在直线y=2x-1上.
由(1)知,当m=1或m=3时,抛物线过点 B(3,5).
把C(0,2)的坐标代入y=x -2mx+m +2m-1,得m +2m-1=2,解得m =1,m = -3.
∴当m=1或-3时,抛物线经过点C(0,2).
如图,当m= -3或m=3时,抛物线与线段 BC只有一个交点;
当m=1时,抛物线同时过点 B,C,不合题意.
∴当-3≤m≤3且m≠1时,抛物线y=x -2mx+m +2m-1与线段BC只有一个交点.
10.【解】(1)∵当y≥0时,-1≤x≤3,
∴x =-1,x =3是方程ax +2x+c=0的两根,A(-1,0),B(3,0),
解得 ∴抛物线的表达式为y=-x +2x+3.
(2)①连接 CD. 把x=2代入y=-x +2x+3得y=3,∴D(2,3).又当x=0时,y=3,∴C(0,3),
∴线段 CD∥x轴.∴CD=2.
∵y= -x +2x+3=-(x-1) +4,
②EM+EN为定值.设D(m,-m +2m+3)(1
由题意可得
解得
∴直线AD的表达式为 y=(3-m)x+(3-m),直线BD的表达式为y= -(m+1)x+3(m+1).
令x=1,得 ∴ME=6-2m,NE=2m+2,∴NE+ME =8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
