第三章 二次函数专题 用二次函数解实际应用问题的六种常见类型(含答案)
文档属性
| 名称 | 第三章 二次函数专题 用二次函数解实际应用问题的六种常见类型(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-26 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章 二次函数
专题 用二次函数解实际应用问题的六种常见类型
类型1 拱桥问题
1.如图①是一座抛物线形拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6m的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点 O 为原点,桥面为x轴建立平面直角坐标系.
(1)求桥拱顶部O 与水面之间的距离.
(2)如图②,桥面上方有3 根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m .
①求出其中一条钢缆所在抛物线的函数表达式;
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
类型2 运动问题
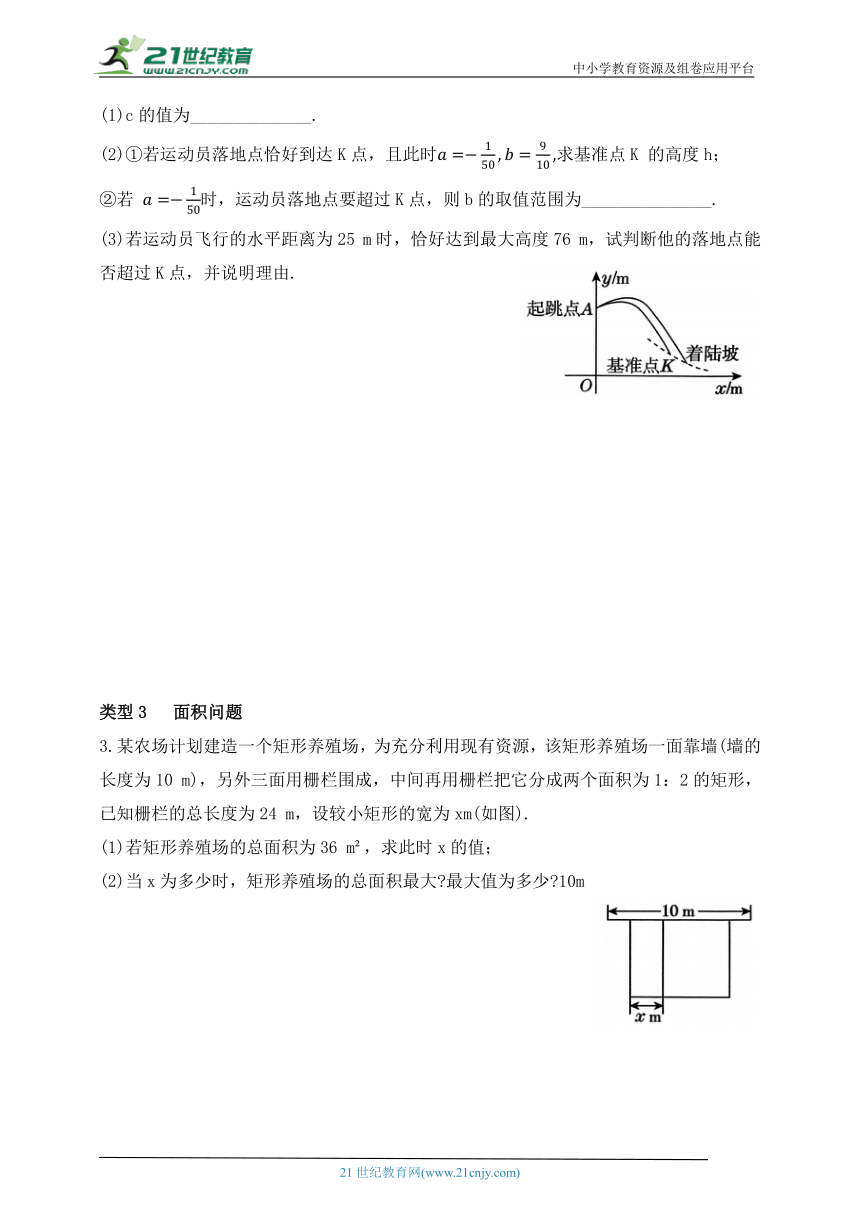
2.跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段,运动员起跳后飞行的路线是抛物线的一部分(如图中实线部分所示),落地点在着陆坡(如图中虚线部分所示)上,着陆坡上的基准点K为飞行距离计分的参照点,落地点超过K点越远,飞行距离分越高.2022年北京冬奥会跳台滑雪标准台的起跳台的高度OA 为66 m,基准点K到起跳台的水平距离为75 m,高度为h m(h为定值).设运动员从起跳点 A起跳后的高度y(m)与水平距离x(m)之间的函数关系为y=ax +bx+c(a≠0).
(1)c的值为______________.
(2)①若运动员落地点恰好到达K点,且此时求基准点K 的高度h;
②若 时,运动员落地点要超过K点,则b的取值范围为_______________.
(3)若运动员飞行的水平距离为25 m时,恰好达到最大高度76 m,试判断他的落地点能否超过K点,并说明理由.
类型3 面积问题
3.某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10 m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1:2的矩形,已知栅栏的总长度为24 m,设较小矩形的宽为xm(如图).
(1)若矩形养殖场的总面积为36 m ,求此时x的值;
(2)当x为多少时,矩形养殖场的总面积最大 最大值为多少 10m
类型4 利润问题
4.打油茶是广西少数民族特有的一种民俗.某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.
(1)求y与x的函数表达式,并写出自变量x的取值范围.
(2)当销售单价定为多少元时,该种油茶的月销售利润最大 求出最大利润.
类型5 灌溉问题
5.如图①,灌溉车沿着平行于绿化带底部边线l的方向行驶,为绿化带浇水,喷水口H离地竖直高度为h(单位:m).如图②,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中二次函数的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3m,竖直高度为 EF的长,下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.5m,灌溉车到l的距离OD为d(单位:m).
(1)若h=1.5,EF=0.5m.
①求上边缘抛物线的函数表达式,并求喷出水的最大射程OC;
②求下边缘抛物线与x轴的正半轴交点 B的坐标;
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求d的取值范围.
(2)若EF=1m,要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出h的最小值.
类型6 决策问题
6.2022年某市接待的游客人数逐月增加,据统计,游玩某景区的游客人数三月为4万人,五月为5.76万人.
(1)求三月到五月,该景区游客人数平均每月的增长率.
(2)若该景区仅有A,B两个景点,售票处出示的三种门票信息如下表所示.
门票种类 甲 乙 丙
可游玩景点 A B A和B
单价 100元 80元 160元
据调查,六月计划购买甲、乙、丙三种门票的人数分别为2万人、3万人和2万人,并且当甲、乙两种门票单价不变时,丙种门票单价每下降1元,有600名原计划购买甲种门票的游客和400名原计划购买乙种门票的游客改为购买丙种门票.
①若丙种门票单价下降10元,求景区六月的门票总收入.
②当丙种门票单价下降多少元时,景区六月的门票总收入有最大值 最大值是多少万元
参考答案
1.【解】(1)根据题意可知点 F的坐标为(6,-1.5),可设桥拱所在抛物线的函数表达式为y =a x .将点F(6,-1.5)的坐标代入y =a x ,解得
当x=12时,
答:桥拱顶部O 与水面之间的距离为6m.
(2)①由题意可知右边钢缆所在抛物线的顶点坐标为(6,1),
设其表达式为y =a (x-6) +1.
将点H(0,4)的坐标代入y =a (x-6) +1,得4=a (0-6) +1,解得
∴右边钢缆所在抛物线的函数表达式为y =
易知左边钢缆所在抛物线的函数表达式为y =
②设彩带的长度为Lm,则 ∴当x=4时,
答:彩带长度的最小值是2m.
2.【解】(1)66
∵基准点K到起跳台的水平距离为75m,
∴基准点K的高度h为21 m.
②
(3)他的落地点能超过K点.理由如下:
∵运动员飞行的水平距离为25 m时,恰好达到最大高度76 m,∴抛物线的顶点为(25,76).
∴抛物线的表达式为y= a(x-25) + 76,把点(0,66)的坐标代入,
得66=a(0-25) +76,解得
∴抛物线的表达式为
当x=75时,
∵36>21,∴他的落地点能超过K点.
3.【解】(1)根据题意知,较大矩形的宽为2xm,长为
∴(x+2x)(8-x)=36,解得x=2或x=6.
经检验,当x=6时,x+2x=18>10不符合题意,舍去,∴x=2,即此时x的值为2.
(2)设矩形养殖场的总面积是ym .
∵墙的长度为10 m2.
根据题意,得y=(x+2x)(8-x)= -3x +24x=-3(x-4) +48.
∵-3<0,∴当 时,y取最大值,最大值为-3×
答:当 时,矩形养殖场的总面积最大,最大值为
4.【解】(1)设函数表达式为y=kx+b.
由题意得 解得 ∴y= -5x+500.
当y=0时,-5x+500=0,解得x=100.
∴y与x的函数表达式为y=-5x+500(50(2)设月销售利润为 w元,则 w=(x-50)(-5x+500)= -5x +750x-25 000=-5(x-75) +3 125.
∵抛物线开口向下,50答:当销售单价定为75元时,该种油茶的月销售利润最大,最大利润是3 125元.
5.【解】(1)①由题意得A(2,2)是上边缘抛物线的顶点.设y=a(x-2) +2.
∵抛物线过点(0,1.5),∴1.5=4a+2,解得
∴上边缘抛物线的函数表达式为
当y=0时 解得x =6,x = -2(舍去).
∴喷出水的最大射程 OC为6m .
②∵上边缘抛物线的对称轴为直线x=2,∴点(0,1.5)关于直线x=2的对称点为(4,1.5).
∴下边缘抛物线是由上边缘抛物线向左平移4m得到的.∴点 B的坐标为(2,0).
③∵EF=0.5m,∴点F的纵坐标为0.5.
令y= 0.5,则 解得
当x>2时,y随x的增大而减小,
∴当2≤x≤6时,要使 y≥0.5,则
∵当0≤x<2时,y随x的增大而增大,且x=0时,y=1.5>0.5,
∴当0≤x≤6时,要使y≥0.5,则(
∵DE=3,要使灌溉车行驶时喷出的水能浇灌到整个绿化带,∴d的最大值为
再看下边缘抛物线,喷出的水能浇灌到绿化带底部的条件是OB≤d,∴d的最小值为2.
综上所述,d的取值范围是
(2)h的最小值为
6.【解】(1)设三月到五月,该景区游客人数平均每月的增长率为x.
由题意,得4(1+x) =5.76,解得x =0.2=20%,x = -2.2(舍去).
答:三月到五月,该景区游客人数平均每月的增长率为20%.
(2)①由题意,得 100×(2-10×0.06)+80×(3-10×0.04)+(160 -10)×(2 + 10×0.06 + 10×0.04)=798(万元).
答:景区六月的门票总收入为798万元.
②设丙种门票单价下降m元,景区六月的门票总收入为W万元.
由题意,得 W=100(2-0.06m)+80(3-0.04m)+(160-m)(2+0.06m+0.04m)= -0.1(m-24) +817.6.易知
∵-0.1<0,∴当m=24时,W取最大值,最大值为817.6.
答:当丙种门票单价下降24元时,景区六月的门票总收入取得最大值,最大值是817.6万元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 二次函数
专题 用二次函数解实际应用问题的六种常见类型
类型1 拱桥问题
1.如图①是一座抛物线形拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6m的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点 O 为原点,桥面为x轴建立平面直角坐标系.
(1)求桥拱顶部O 与水面之间的距离.
(2)如图②,桥面上方有3 根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m .
①求出其中一条钢缆所在抛物线的函数表达式;
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
类型2 运动问题
2.跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段,运动员起跳后飞行的路线是抛物线的一部分(如图中实线部分所示),落地点在着陆坡(如图中虚线部分所示)上,着陆坡上的基准点K为飞行距离计分的参照点,落地点超过K点越远,飞行距离分越高.2022年北京冬奥会跳台滑雪标准台的起跳台的高度OA 为66 m,基准点K到起跳台的水平距离为75 m,高度为h m(h为定值).设运动员从起跳点 A起跳后的高度y(m)与水平距离x(m)之间的函数关系为y=ax +bx+c(a≠0).
(1)c的值为______________.
(2)①若运动员落地点恰好到达K点,且此时求基准点K 的高度h;
②若 时,运动员落地点要超过K点,则b的取值范围为_______________.
(3)若运动员飞行的水平距离为25 m时,恰好达到最大高度76 m,试判断他的落地点能否超过K点,并说明理由.
类型3 面积问题
3.某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10 m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1:2的矩形,已知栅栏的总长度为24 m,设较小矩形的宽为xm(如图).
(1)若矩形养殖场的总面积为36 m ,求此时x的值;
(2)当x为多少时,矩形养殖场的总面积最大 最大值为多少 10m
类型4 利润问题
4.打油茶是广西少数民族特有的一种民俗.某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.
(1)求y与x的函数表达式,并写出自变量x的取值范围.
(2)当销售单价定为多少元时,该种油茶的月销售利润最大 求出最大利润.
类型5 灌溉问题
5.如图①,灌溉车沿着平行于绿化带底部边线l的方向行驶,为绿化带浇水,喷水口H离地竖直高度为h(单位:m).如图②,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中二次函数的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3m,竖直高度为 EF的长,下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.5m,灌溉车到l的距离OD为d(单位:m).
(1)若h=1.5,EF=0.5m.
①求上边缘抛物线的函数表达式,并求喷出水的最大射程OC;
②求下边缘抛物线与x轴的正半轴交点 B的坐标;
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求d的取值范围.
(2)若EF=1m,要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出h的最小值.
类型6 决策问题
6.2022年某市接待的游客人数逐月增加,据统计,游玩某景区的游客人数三月为4万人,五月为5.76万人.
(1)求三月到五月,该景区游客人数平均每月的增长率.
(2)若该景区仅有A,B两个景点,售票处出示的三种门票信息如下表所示.
门票种类 甲 乙 丙
可游玩景点 A B A和B
单价 100元 80元 160元
据调查,六月计划购买甲、乙、丙三种门票的人数分别为2万人、3万人和2万人,并且当甲、乙两种门票单价不变时,丙种门票单价每下降1元,有600名原计划购买甲种门票的游客和400名原计划购买乙种门票的游客改为购买丙种门票.
①若丙种门票单价下降10元,求景区六月的门票总收入.
②当丙种门票单价下降多少元时,景区六月的门票总收入有最大值 最大值是多少万元
参考答案
1.【解】(1)根据题意可知点 F的坐标为(6,-1.5),可设桥拱所在抛物线的函数表达式为y =a x .将点F(6,-1.5)的坐标代入y =a x ,解得
当x=12时,
答:桥拱顶部O 与水面之间的距离为6m.
(2)①由题意可知右边钢缆所在抛物线的顶点坐标为(6,1),
设其表达式为y =a (x-6) +1.
将点H(0,4)的坐标代入y =a (x-6) +1,得4=a (0-6) +1,解得
∴右边钢缆所在抛物线的函数表达式为y =
易知左边钢缆所在抛物线的函数表达式为y =
②设彩带的长度为Lm,则 ∴当x=4时,
答:彩带长度的最小值是2m.
2.【解】(1)66
∵基准点K到起跳台的水平距离为75m,
∴基准点K的高度h为21 m.
②
(3)他的落地点能超过K点.理由如下:
∵运动员飞行的水平距离为25 m时,恰好达到最大高度76 m,∴抛物线的顶点为(25,76).
∴抛物线的表达式为y= a(x-25) + 76,把点(0,66)的坐标代入,
得66=a(0-25) +76,解得
∴抛物线的表达式为
当x=75时,
∵36>21,∴他的落地点能超过K点.
3.【解】(1)根据题意知,较大矩形的宽为2xm,长为
∴(x+2x)(8-x)=36,解得x=2或x=6.
经检验,当x=6时,x+2x=18>10不符合题意,舍去,∴x=2,即此时x的值为2.
(2)设矩形养殖场的总面积是ym .
∵墙的长度为10 m2.
根据题意,得y=(x+2x)(8-x)= -3x +24x=-3(x-4) +48.
∵-3<0,∴当 时,y取最大值,最大值为-3×
答:当 时,矩形养殖场的总面积最大,最大值为
4.【解】(1)设函数表达式为y=kx+b.
由题意得 解得 ∴y= -5x+500.
当y=0时,-5x+500=0,解得x=100.
∴y与x的函数表达式为y=-5x+500(50
∵抛物线开口向下,50
5.【解】(1)①由题意得A(2,2)是上边缘抛物线的顶点.设y=a(x-2) +2.
∵抛物线过点(0,1.5),∴1.5=4a+2,解得
∴上边缘抛物线的函数表达式为
当y=0时 解得x =6,x = -2(舍去).
∴喷出水的最大射程 OC为6m .
②∵上边缘抛物线的对称轴为直线x=2,∴点(0,1.5)关于直线x=2的对称点为(4,1.5).
∴下边缘抛物线是由上边缘抛物线向左平移4m得到的.∴点 B的坐标为(2,0).
③∵EF=0.5m,∴点F的纵坐标为0.5.
令y= 0.5,则 解得
当x>2时,y随x的增大而减小,
∴当2≤x≤6时,要使 y≥0.5,则
∵当0≤x<2时,y随x的增大而增大,且x=0时,y=1.5>0.5,
∴当0≤x≤6时,要使y≥0.5,则(
∵DE=3,要使灌溉车行驶时喷出的水能浇灌到整个绿化带,∴d的最大值为
再看下边缘抛物线,喷出的水能浇灌到绿化带底部的条件是OB≤d,∴d的最小值为2.
综上所述,d的取值范围是
(2)h的最小值为
6.【解】(1)设三月到五月,该景区游客人数平均每月的增长率为x.
由题意,得4(1+x) =5.76,解得x =0.2=20%,x = -2.2(舍去).
答:三月到五月,该景区游客人数平均每月的增长率为20%.
(2)①由题意,得 100×(2-10×0.06)+80×(3-10×0.04)+(160 -10)×(2 + 10×0.06 + 10×0.04)=798(万元).
答:景区六月的门票总收入为798万元.
②设丙种门票单价下降m元,景区六月的门票总收入为W万元.
由题意,得 W=100(2-0.06m)+80(3-0.04m)+(160-m)(2+0.06m+0.04m)= -0.1(m-24) +817.6.易知
∵-0.1<0,∴当m=24时,W取最大值,最大值为817.6.
答:当丙种门票单价下降24元时,景区六月的门票总收入取得最大值,最大值是817.6万元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
