1.3.2有理数的减法(第二课时) 课件(共24张PPT)
文档属性
| 名称 | 1.3.2有理数的减法(第二课时) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 10:05:08 | ||
图片预览








文档简介
(共24张PPT)
新课标 人教版 七年级上册
2023-2024学年度上学期人教版精品课件
第一章有理数
1.3.2有理数的减法(第二课时)
有理数加减混合运算
学习目标
1. 理解有理数加减法混合运算统一转化为有理数加法运算的依据——有理数减法法则.
2. 掌握有理数的加减混合运算及其运算顺序,熟练运用有理数加法、减法运算法则进行加减混合运算,培养运算能力和转化思想.
3.理解有理数减法运算可以表示数轴上两点之间距离,体会数形结合思想的应用.
复习提问
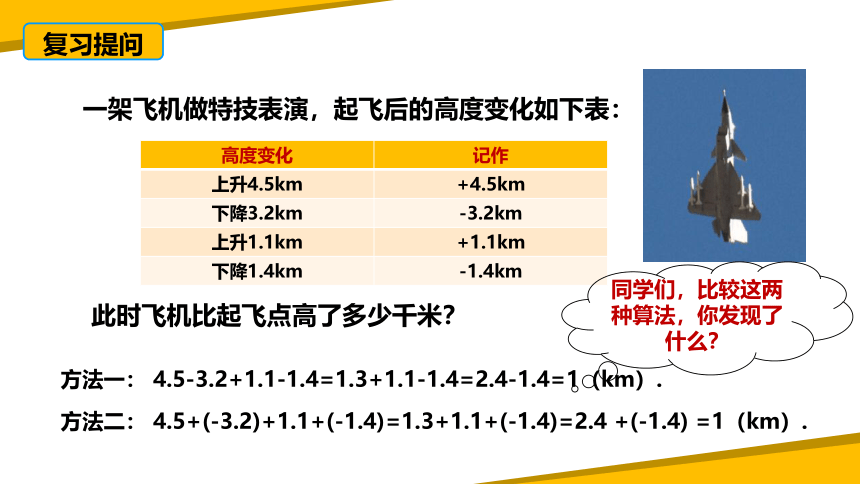
一架飞机做特技表演,起飞后的高度变化如下表:
此时飞机比起飞点高了多少千米?
高度变化 记作
上升4.5km +4.5km
下降3.2km -3.2km
上升1.1km +1.1km
下降1.4km -1.4km
方法一: 4.5-3.2+1.1-1.4=1.3+1.1-1.4=2.4-1.4=1(km).
方法二: 4.5+(-3.2)+1.1+(-1.4)=1.3+1.1+(-1.4)=2.4 +(-1.4) =1(km).
同学们,比较这两种算法,你发现了什么?
探究新知
省略了加号和括号
把4.5-3.2+1.1-1.4看作为4.5,-3.2,1.1,-1.4的和,
也叫“代数和”.
4.5+(-3.2)+1.1+(-1.4)
4.5-3.2+1.1-1.4
探究新知
有理数的加减混合运算可以统一成加法运算。
省略括号和前面的加号
注意:有理数的加法运算可以写成省略括号及前面加号的形式.
探究新知
(-20)+(+3)+(+5)+(-7)
这个算式中有加法,也有减法. 可以根据有理数减法法则,把它改写为
分析:
使问题转化为几个有理数的加法.
例1:计算 (-20)+(+3)-(-5)-(+7).
探究新知
解:
这里使用了哪些运算律?
有理数加法的交换律、结合律
要点归纳:引入相反数后,加减混合运算可以统一为加法运算:
方法1:(把加减混合运算统一成加法运算)
探究新知
算式 是 , , , 这四个数的和.
为书写简单,省略算式中的括号和加号写为 .
我们可以读作 的和,
或读作 加 加 减 .
- 20 3 5 - 7
-20+3+5 - 7
负20、 正3、正5、负7
负20 3 5 7
探究新知
例1:计算 (-20)+(+3)-(-5)-(+7).
解:
方法2:(省略括号和前面的加号)
建立模型
例题2:计算
(把加减混合运算统一成加法运算)
(加法交换律)
注意:在有理数加减混合运算过程中,交换加数位置时,要连同加数前面的符号一起交换.
方法一:减法变加法
探究新知
(加法交换律)
例题2:计算
(省略括号和前面的加号)
方法二:去括号法
典例解析
有理数加减混合运算的步骤:
1. 将减法转化为加法运算;
2. 省略加号和括号;
3. 运用加法交换律和结合律,将同号两数相加;
4. 按有理数加法法则计算.
随堂练习
计算:
拓展应用
数轴上两点之间的距离
在数轴上,点A、B分别表示数a,b ,利用有理数减法分别计算
下列情况下点A、B之间的距离:
a=2,b=6;a=0,b=6;a=2,b=-6;a=-2,b=-6.
你能否发现A,B之间的距离与数a,b之间的关系吗?
拓展应用
数轴上两点之间的距离
0
B
A
在数轴上,点A、B分别表示数a,b ,利用有理数减法法则探究:点A、B之间的距离与a,b的关系.
结论:
用数来刻画直线上两点之间的距离.
数形结合思想
中考链接
课堂小结
步骤
方法一:减法转化成加法
方法二:省略括号法
有理数加减法混合运算
核心素养
数形结合:同一数轴上两点间距离公式
转化思想:
运算能力:
减法
加法
转化
法则
有理数的加法法则
有理数的减法法则
运算律
当堂测试
当堂测试
分层作业
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 七年级上册
2023-2024学年度上学期人教版精品课件
第一章有理数
1.3.2有理数的减法(第二课时)
有理数加减混合运算
学习目标
1. 理解有理数加减法混合运算统一转化为有理数加法运算的依据——有理数减法法则.
2. 掌握有理数的加减混合运算及其运算顺序,熟练运用有理数加法、减法运算法则进行加减混合运算,培养运算能力和转化思想.
3.理解有理数减法运算可以表示数轴上两点之间距离,体会数形结合思想的应用.
复习提问
一架飞机做特技表演,起飞后的高度变化如下表:
此时飞机比起飞点高了多少千米?
高度变化 记作
上升4.5km +4.5km
下降3.2km -3.2km
上升1.1km +1.1km
下降1.4km -1.4km
方法一: 4.5-3.2+1.1-1.4=1.3+1.1-1.4=2.4-1.4=1(km).
方法二: 4.5+(-3.2)+1.1+(-1.4)=1.3+1.1+(-1.4)=2.4 +(-1.4) =1(km).
同学们,比较这两种算法,你发现了什么?
探究新知
省略了加号和括号
把4.5-3.2+1.1-1.4看作为4.5,-3.2,1.1,-1.4的和,
也叫“代数和”.
4.5+(-3.2)+1.1+(-1.4)
4.5-3.2+1.1-1.4
探究新知
有理数的加减混合运算可以统一成加法运算。
省略括号和前面的加号
注意:有理数的加法运算可以写成省略括号及前面加号的形式.
探究新知
(-20)+(+3)+(+5)+(-7)
这个算式中有加法,也有减法. 可以根据有理数减法法则,把它改写为
分析:
使问题转化为几个有理数的加法.
例1:计算 (-20)+(+3)-(-5)-(+7).
探究新知
解:
这里使用了哪些运算律?
有理数加法的交换律、结合律
要点归纳:引入相反数后,加减混合运算可以统一为加法运算:
方法1:(把加减混合运算统一成加法运算)
探究新知
算式 是 , , , 这四个数的和.
为书写简单,省略算式中的括号和加号写为 .
我们可以读作 的和,
或读作 加 加 减 .
- 20 3 5 - 7
-20+3+5 - 7
负20、 正3、正5、负7
负20 3 5 7
探究新知
例1:计算 (-20)+(+3)-(-5)-(+7).
解:
方法2:(省略括号和前面的加号)
建立模型
例题2:计算
(把加减混合运算统一成加法运算)
(加法交换律)
注意:在有理数加减混合运算过程中,交换加数位置时,要连同加数前面的符号一起交换.
方法一:减法变加法
探究新知
(加法交换律)
例题2:计算
(省略括号和前面的加号)
方法二:去括号法
典例解析
有理数加减混合运算的步骤:
1. 将减法转化为加法运算;
2. 省略加号和括号;
3. 运用加法交换律和结合律,将同号两数相加;
4. 按有理数加法法则计算.
随堂练习
计算:
拓展应用
数轴上两点之间的距离
在数轴上,点A、B分别表示数a,b ,利用有理数减法分别计算
下列情况下点A、B之间的距离:
a=2,b=6;a=0,b=6;a=2,b=-6;a=-2,b=-6.
你能否发现A,B之间的距离与数a,b之间的关系吗?
拓展应用
数轴上两点之间的距离
0
B
A
在数轴上,点A、B分别表示数a,b ,利用有理数减法法则探究:点A、B之间的距离与a,b的关系.
结论:
用数来刻画直线上两点之间的距离.
数形结合思想
中考链接
课堂小结
步骤
方法一:减法转化成加法
方法二:省略括号法
有理数加减法混合运算
核心素养
数形结合:同一数轴上两点间距离公式
转化思想:
运算能力:
减法
加法
转化
法则
有理数的加法法则
有理数的减法法则
运算律
当堂测试
当堂测试
分层作业
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
