第11章三角形 同步练习题 2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 第11章三角形 同步练习题 2023—2024学年人教版数学八年级上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 281.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 00:00:00 | ||
图片预览



文档简介
2023-2024学年人教版八年级数学上册《第11章三角形》同步练习题(附答案)
一、单选题
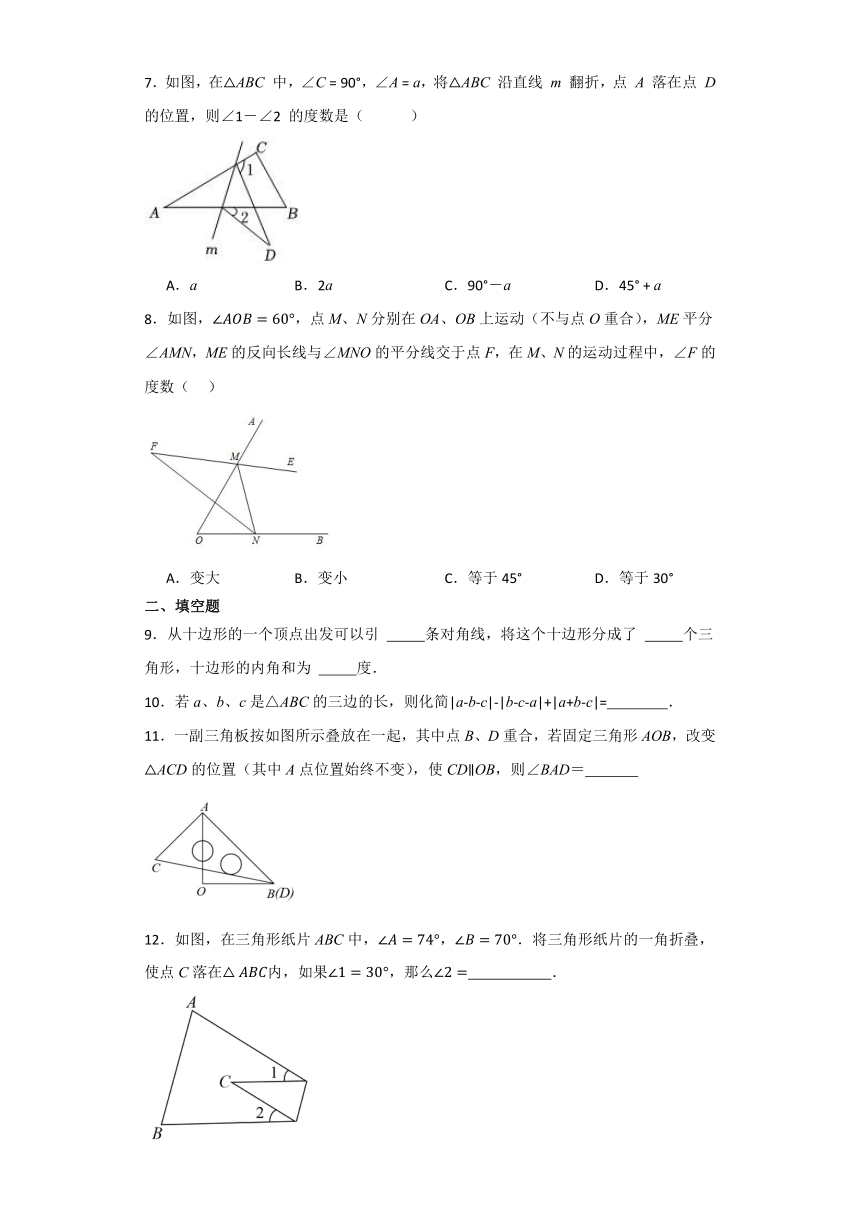
1.已知三角形的两边长分别为和,则该三角形的第三边的长度可能是( )
A. B. C. D.
2.下列说法不正确的是( )
A.三角形的三条高线交于一点 B.直角三角形有三条高
C.三角形的三条角平分线交于一点 D.三角形的三条中线交于一点
3.在下列图形中,正确画出△ABC的AC边上的高的图形是( )
A. B.
C. D.
4.如图,中,D、E、F分别为BC、AD、BE的中点,且,则阴影部分面积为 .
A.8 B.6 C.4 D.2
5.已知 AD 是△ABC 的一条高,∠BAD=70°,∠CAD=20°,则∠BAC 的度数为( )
A.50° B.60° C.90° D.50°或 90°
6.如图,正五边形ABCDE,对角线AC、BD交于点P,那么∠APD=( )
A.96° B.100° C.108° D.115°
7.如图,在△ABC 中,∠C = 90°,∠A = a,将△ABC 沿直线 m 翻折,点 A 落在点 D 的位置,则∠1-∠2 的度数是( )
A.a B.2a C.90°-a D.45° + a
8.如图,,点M、N分别在OA、OB上运动(不与点O重合),ME平分∠AMN,ME的反向长线与∠MNO的平分线交于点F,在M、N的运动过程中,∠F的度数( )
A.变大 B.变小 C.等于45° D.等于30°
二、填空题
9.从十边形的一个顶点出发可以引 条对角线,将这个十边形分成了 个三角形,十边形的内角和为 度.
10.若a、b、c是△ABC的三边的长,则化简|a-b-c|-|b-c-a|+|a+b-c|= .
11.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变△ACD的位置(其中A点位置始终不变),使CDOB,则∠BAD=
12.如图,在三角形纸片ABC中,.将三角形纸片的一角折叠,使点C落在内,如果,那么 .
13.在△ABC中,高BD和CE所在直线相交于点O,若△ABC不是直角三角形,且∠A=50°,则∠BOC=
14.如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,以每秒2cm的速度沿A→C→E运动.若设点P运动的时间是t秒,那么当t= 时,△APE的面积等于8.
15.如图,一轮船由B处向C处航行,在B处测得C处在B处的北偏东75°方向上,在海岛上的观察所A测得B在A的南偏西30°方向上,C在A的南偏东25°方向.若轮船行驶到C处,那么从C处看A,B两处的视角∠ACB= .
16.如图,∠A=120°,且∠1=∠2=∠3和∠4=∠5=∠6,则∠BDE= .
三、解答题
17.已知一个三角形的三边长分别为,,5,求整数a的值.
18.如图,在中,,平分,为(不与点,重合)上一点,于点.若,,求的度数.
19.如图,已知,分别是的高和中线,,,,.试求:
(1)的长;
(2)的面积;
(3)和的周长差.
20.如图,在中,平分,点为线段上的一个动点,交的延长线于点.
(1)若,,求的度数;
(2)若,且,求的度数.
21.在中,平分,点P为直线上一动点,于点O.
(1)如图①,当,,点P与点C重合时,_______.
(2)如图②,当点P在的延长线上时,求证:;
22.小明在学习过程中,对教材中的一个有趣问题做如下探究:
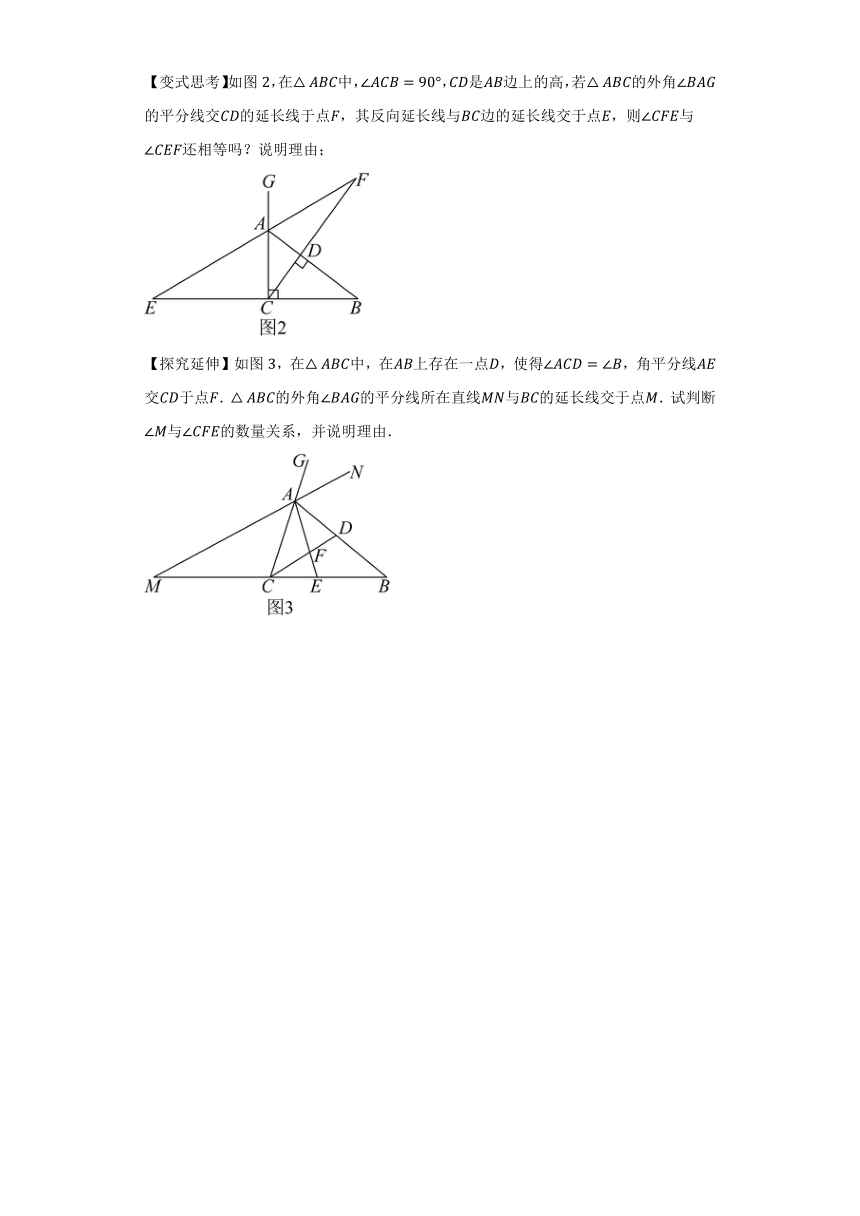
【习题回顾】已知:如图,在中,,是角平分线,是高,、相交于点.求证:;
【变式思考】如图,在中,,是边上的高,若的外角的平分线交的延长线于点,其反向延长线与边的延长线交于点,则与还相等吗?说明理由;
【探究延伸】如图,在中,在上存在一点,使得,角平分线交于点.的外角的平分线所在直线与的延长线交于点.试判断与的数量关系,并说明理由.
参考答案
1.解:设第三边的长为x cm,根据三角形的三边关系,
得5-3<x<5+3,即2<x<8.
故选:B.
2.解:A、三角形的三条高线所在的直线交于一点,错误;
B、直角三角形有三条高,正确;
C、三角形的三条角平分线交于一点,正确;
D、三角形的三条中线交于一点,正确;
故选A.
3.解:△ABC的AC边上的高的就是通过顶点B作的AC所在直线的垂线段.根据定义正确的只有C.
故选C.
4.解:∵S△ABC=16cm2,AD是△ABC的中线,∴S△ABD=8cm2.
∵BE是△ABD的中线,∴S△BED=4cm2.
∵DF是△BDE的中线,∴S△EFD=2cm2.
故选D.
5.解:当 AD 在三角形的内部时,∠BAC=∠BAD+∠CAD=90°; 当 AD 在三角形的外部时,∠BAC=∠BAD﹣∠CAD=50°.
故选D.
6.解:∵五边形ABCDE为正五边形,
∴AB=BC=CD,∠ABC=∠BCD=108°,
∴∠BAC=∠BCA=∠CBD=∠BDC==36°,
∴∠APD=∠BPC=180°﹣∠CBD﹣∠BCA=180°﹣36°﹣36°=108°.
故选:C.
7.解:如图,
∵∠1=∠A+∠AEF,又∠AEF=∠2+∠D,
∴∠1=∠A+∠2+∠D.
由折叠得∠A=∠D=a,
∴∠1=∠A+∠2+∠D=2a+∠2,
∴∠1-∠2=2a.
故选:B.
8.解:∵ME平分,NF平分,
∴,,
∵,
∴,
∵,
∴,
又∵,
∴,
故选:D.
9.解:从n边形的一个顶点出发可以引(n﹣3)条对角线,这些对角线将这个多边形分成(n﹣2)个三角形,
∴从十边形的一个顶点出发可以画出7条对角线,这些对角线将十边形分割成8个三角形,
十边形的内角和为:(10﹣2)×180°=1440°,
故答案为:7;8;1440.
10.解:∵a,b,c是△ABC的三边,
∴a<b+c,b<c+a,c<a+b,
∴a b c<0,b c a<0,c+a b>0,
∴|a-b-c|-|b-c-a|+|a+b-c|==.
故答案为:
11.解:设∠BAD=α,
∵CDOB,
∴∠AEC=∠B=45°,
∵∠D=30°,
∴α=∠BAD=45°-30°=15°,
∴当α=15°时,CDOB,
∴∠BAD=15°,
当CD在点A的上方时,
DC边与OB边平行时,
∴∠CEA=∠B=45°,
∴∠DAE=∠CEA-∠D=45°-30°=15°,
∴α=∠BAD=180°-15°=165°,
∠BAD=135°+30°=165°,
故答案为:15°或165°.
12.解:如图延长AE、BF交于点,连接C.
在△AB中,∠AB=180° 74° 70°=36°,
∵∠ECF=∠AB=36°,∠1=∠EC+∠EC,∠2=∠FC+∠FC,
∴∠1+∠2=∠EC+∠EC+∠FC+∠FC=2∠AB=72°,
∵∠1=30°,
∴∠2=42°,
故答案为:42°.
13.解:分两种情况:
①如图1,△ABC是锐角三角形时,
∵BD、CE是高,
∴∠ADO=∠AEO=90°,
∴∠DOE=360° ∠A ∠ADO ∠AEO=360° 50° 90° 90°=130°,
∴∠BOC=∠DOE=130°;
②如图2,△ABC是钝角三角形时,
∵BD、CE是高,
∴∠ADO=∠AEO=90°,
∴∠A+∠ACE=90°,∠BOC+∠DCO=90°,
∵∠ACE=∠DCO,
∴∠BOC=∠A=50°,
综上所述,∠BOC为130°或50°.
故答案为:130°或50°.
14.解:∵BC=8cm,点E是BC的中点,
∴CE=BC=4cm,
当点P在线段AC上,如图1所示,AP=2t,
∵∠C=90°,
∴S△APE=AP CE=×2t×4= 4t=8,
解得:t=2;
当点P在线段CE上,如图2所示,AC=6cm,PE=10-2t,
∴S△APE=PE AC=×(10-2t)×6=8,
解得:t=.
故答案为∶ 2或.
15.解:如图,由题意得:∠DBC=75°,∠BAE=30°,∠EAC=25°,BDAE,
∴∠ABD=∠BAE=30°,∠BAC=∠BAE+∠EAC=55°,
∴∠ABC=∠DBC ∠ABD=75° 30°=45°,
∴∠ACB=180° ∠ABC ∠BAC=180° 45° 55°=80°,
故答案为:80°.
16.解:在中,,
,,
,
、分别是、的角平分线,
平分,
而,
.
故答案为:.
17.解:依题意得,
解得:,
a为整数,
,
即整数a的值为3.
18.解:,,
,
,
是的平分线,
,
∴.
19.(1)解:∵,是边上的高,
∴ ,
∴,
即的长度为;
(2)解:如图,∵是直角三角形,,,,
∴,
又∵是边的中线,
∴,
∴,即,
∴.
∴的面积是;
(3)解:∵是边的中线,
∴,
∴的周长﹣的周长 ,
即和的周长的差是.
20.(1)解:,,.
.
平分.
.
.
又.
.
.
;
(2)平分,
,
,
,
设,
,
,
,
,
,
,
,
,
.
21.(1)解:(1)∵,,
∴,
∵平分,
∴,
∵,
∴,
∴;
故答案为:10°
(2)连接并延长.
∵,,
∴,
∵,
∴
∴,
∴.
∵平分,
∴.
∵,
∴
∴
∴
∴
22.解:[习题回顾]:证明:,是高,
,,
,
是角平分线,
,
,
;
[变式思考]
证明:为的角平分线,
,
为边上的高,
,
,
,
又,
;
[探究延伸]
,
证明:、、三点共线,、为角平分线,
,,
又,
,
,
,
,,,
,
.
一、单选题
1.已知三角形的两边长分别为和,则该三角形的第三边的长度可能是( )
A. B. C. D.
2.下列说法不正确的是( )
A.三角形的三条高线交于一点 B.直角三角形有三条高
C.三角形的三条角平分线交于一点 D.三角形的三条中线交于一点
3.在下列图形中,正确画出△ABC的AC边上的高的图形是( )
A. B.
C. D.
4.如图,中,D、E、F分别为BC、AD、BE的中点,且,则阴影部分面积为 .
A.8 B.6 C.4 D.2
5.已知 AD 是△ABC 的一条高,∠BAD=70°,∠CAD=20°,则∠BAC 的度数为( )
A.50° B.60° C.90° D.50°或 90°
6.如图,正五边形ABCDE,对角线AC、BD交于点P,那么∠APD=( )
A.96° B.100° C.108° D.115°
7.如图,在△ABC 中,∠C = 90°,∠A = a,将△ABC 沿直线 m 翻折,点 A 落在点 D 的位置,则∠1-∠2 的度数是( )
A.a B.2a C.90°-a D.45° + a
8.如图,,点M、N分别在OA、OB上运动(不与点O重合),ME平分∠AMN,ME的反向长线与∠MNO的平分线交于点F,在M、N的运动过程中,∠F的度数( )
A.变大 B.变小 C.等于45° D.等于30°
二、填空题
9.从十边形的一个顶点出发可以引 条对角线,将这个十边形分成了 个三角形,十边形的内角和为 度.
10.若a、b、c是△ABC的三边的长,则化简|a-b-c|-|b-c-a|+|a+b-c|= .
11.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变△ACD的位置(其中A点位置始终不变),使CDOB,则∠BAD=
12.如图,在三角形纸片ABC中,.将三角形纸片的一角折叠,使点C落在内,如果,那么 .
13.在△ABC中,高BD和CE所在直线相交于点O,若△ABC不是直角三角形,且∠A=50°,则∠BOC=
14.如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,以每秒2cm的速度沿A→C→E运动.若设点P运动的时间是t秒,那么当t= 时,△APE的面积等于8.
15.如图,一轮船由B处向C处航行,在B处测得C处在B处的北偏东75°方向上,在海岛上的观察所A测得B在A的南偏西30°方向上,C在A的南偏东25°方向.若轮船行驶到C处,那么从C处看A,B两处的视角∠ACB= .
16.如图,∠A=120°,且∠1=∠2=∠3和∠4=∠5=∠6,则∠BDE= .
三、解答题
17.已知一个三角形的三边长分别为,,5,求整数a的值.
18.如图,在中,,平分,为(不与点,重合)上一点,于点.若,,求的度数.
19.如图,已知,分别是的高和中线,,,,.试求:
(1)的长;
(2)的面积;
(3)和的周长差.
20.如图,在中,平分,点为线段上的一个动点,交的延长线于点.
(1)若,,求的度数;
(2)若,且,求的度数.
21.在中,平分,点P为直线上一动点,于点O.
(1)如图①,当,,点P与点C重合时,_______.
(2)如图②,当点P在的延长线上时,求证:;
22.小明在学习过程中,对教材中的一个有趣问题做如下探究:
【习题回顾】已知:如图,在中,,是角平分线,是高,、相交于点.求证:;
【变式思考】如图,在中,,是边上的高,若的外角的平分线交的延长线于点,其反向延长线与边的延长线交于点,则与还相等吗?说明理由;
【探究延伸】如图,在中,在上存在一点,使得,角平分线交于点.的外角的平分线所在直线与的延长线交于点.试判断与的数量关系,并说明理由.
参考答案
1.解:设第三边的长为x cm,根据三角形的三边关系,
得5-3<x<5+3,即2<x<8.
故选:B.
2.解:A、三角形的三条高线所在的直线交于一点,错误;
B、直角三角形有三条高,正确;
C、三角形的三条角平分线交于一点,正确;
D、三角形的三条中线交于一点,正确;
故选A.
3.解:△ABC的AC边上的高的就是通过顶点B作的AC所在直线的垂线段.根据定义正确的只有C.
故选C.
4.解:∵S△ABC=16cm2,AD是△ABC的中线,∴S△ABD=8cm2.
∵BE是△ABD的中线,∴S△BED=4cm2.
∵DF是△BDE的中线,∴S△EFD=2cm2.
故选D.
5.解:当 AD 在三角形的内部时,∠BAC=∠BAD+∠CAD=90°; 当 AD 在三角形的外部时,∠BAC=∠BAD﹣∠CAD=50°.
故选D.
6.解:∵五边形ABCDE为正五边形,
∴AB=BC=CD,∠ABC=∠BCD=108°,
∴∠BAC=∠BCA=∠CBD=∠BDC==36°,
∴∠APD=∠BPC=180°﹣∠CBD﹣∠BCA=180°﹣36°﹣36°=108°.
故选:C.
7.解:如图,
∵∠1=∠A+∠AEF,又∠AEF=∠2+∠D,
∴∠1=∠A+∠2+∠D.
由折叠得∠A=∠D=a,
∴∠1=∠A+∠2+∠D=2a+∠2,
∴∠1-∠2=2a.
故选:B.
8.解:∵ME平分,NF平分,
∴,,
∵,
∴,
∵,
∴,
又∵,
∴,
故选:D.
9.解:从n边形的一个顶点出发可以引(n﹣3)条对角线,这些对角线将这个多边形分成(n﹣2)个三角形,
∴从十边形的一个顶点出发可以画出7条对角线,这些对角线将十边形分割成8个三角形,
十边形的内角和为:(10﹣2)×180°=1440°,
故答案为:7;8;1440.
10.解:∵a,b,c是△ABC的三边,
∴a<b+c,b<c+a,c<a+b,
∴a b c<0,b c a<0,c+a b>0,
∴|a-b-c|-|b-c-a|+|a+b-c|==.
故答案为:
11.解:设∠BAD=α,
∵CDOB,
∴∠AEC=∠B=45°,
∵∠D=30°,
∴α=∠BAD=45°-30°=15°,
∴当α=15°时,CDOB,
∴∠BAD=15°,
当CD在点A的上方时,
DC边与OB边平行时,
∴∠CEA=∠B=45°,
∴∠DAE=∠CEA-∠D=45°-30°=15°,
∴α=∠BAD=180°-15°=165°,
∠BAD=135°+30°=165°,
故答案为:15°或165°.
12.解:如图延长AE、BF交于点,连接C.
在△AB中,∠AB=180° 74° 70°=36°,
∵∠ECF=∠AB=36°,∠1=∠EC+∠EC,∠2=∠FC+∠FC,
∴∠1+∠2=∠EC+∠EC+∠FC+∠FC=2∠AB=72°,
∵∠1=30°,
∴∠2=42°,
故答案为:42°.
13.解:分两种情况:
①如图1,△ABC是锐角三角形时,
∵BD、CE是高,
∴∠ADO=∠AEO=90°,
∴∠DOE=360° ∠A ∠ADO ∠AEO=360° 50° 90° 90°=130°,
∴∠BOC=∠DOE=130°;
②如图2,△ABC是钝角三角形时,
∵BD、CE是高,
∴∠ADO=∠AEO=90°,
∴∠A+∠ACE=90°,∠BOC+∠DCO=90°,
∵∠ACE=∠DCO,
∴∠BOC=∠A=50°,
综上所述,∠BOC为130°或50°.
故答案为:130°或50°.
14.解:∵BC=8cm,点E是BC的中点,
∴CE=BC=4cm,
当点P在线段AC上,如图1所示,AP=2t,
∵∠C=90°,
∴S△APE=AP CE=×2t×4= 4t=8,
解得:t=2;
当点P在线段CE上,如图2所示,AC=6cm,PE=10-2t,
∴S△APE=PE AC=×(10-2t)×6=8,
解得:t=.
故答案为∶ 2或.
15.解:如图,由题意得:∠DBC=75°,∠BAE=30°,∠EAC=25°,BDAE,
∴∠ABD=∠BAE=30°,∠BAC=∠BAE+∠EAC=55°,
∴∠ABC=∠DBC ∠ABD=75° 30°=45°,
∴∠ACB=180° ∠ABC ∠BAC=180° 45° 55°=80°,
故答案为:80°.
16.解:在中,,
,,
,
、分别是、的角平分线,
平分,
而,
.
故答案为:.
17.解:依题意得,
解得:,
a为整数,
,
即整数a的值为3.
18.解:,,
,
,
是的平分线,
,
∴.
19.(1)解:∵,是边上的高,
∴ ,
∴,
即的长度为;
(2)解:如图,∵是直角三角形,,,,
∴,
又∵是边的中线,
∴,
∴,即,
∴.
∴的面积是;
(3)解:∵是边的中线,
∴,
∴的周长﹣的周长 ,
即和的周长的差是.
20.(1)解:,,.
.
平分.
.
.
又.
.
.
;
(2)平分,
,
,
,
设,
,
,
,
,
,
,
,
,
.
21.(1)解:(1)∵,,
∴,
∵平分,
∴,
∵,
∴,
∴;
故答案为:10°
(2)连接并延长.
∵,,
∴,
∵,
∴
∴,
∴.
∵平分,
∴.
∵,
∴
∴
∴
∴
22.解:[习题回顾]:证明:,是高,
,,
,
是角平分线,
,
,
;
[变式思考]
证明:为的角平分线,
,
为边上的高,
,
,
,
又,
;
[探究延伸]
,
证明:、、三点共线,、为角平分线,
,,
又,
,
,
,
,,,
,
.
