2023—2024学年人教版数学八年级上册11.3多边形及其内角和 同步练习题(含解析)
文档属性
| 名称 | 2023—2024学年人教版数学八年级上册11.3多边形及其内角和 同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 455.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 15:48:12 | ||
图片预览




文档简介
2023-2024学年人教版八年级数学上册《11.3多边形及其内角和》同步练习题(附答案)
一、单选题
1.若一个多边形的每个内角均是120°,则这个多边形的边数为( )
A.9 B.8 C.7 D.6
2.一个多边形的内角和是,那么这个多边形的对角线的条数是( )
A.2 B.3 C.4 D.5
3.已知一个多边形的内角和与外角和的和为1980°,这个多边形的边数为( )
A.9 B.10 C.11 D.12
4.将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540° C.720° D.730°
5.某中学新科技馆铺设地面,已有正方形地砖,现打算购买另一种正多边形地砖(边长与正方形的相等),与正方形地砖作平面镶嵌,则该学校可以购买的地砖形状是( )
A.正五边形 B.正六边形 C.正八边形 D.正十二边形
6.如图所示,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2的度数为( )
A.135° B.240° C.270° D.300°
7.在计算一个多边形的内角和时,由于粗心少算了1个内角,其和等于1180°,则少算的这个角的度数是( )
A.60 B.70 C.80 D.90
8.如图,( ).
A.180° B.270° C.360° D.540°
二、填空题
9.从某个多边形的一个顶点可以引出3条对角线,则这个多边形内角和的度数为 .
10.一个正多边形的每一个内角比每一个外角的5倍还小60°,则这个正多边形的内角和是 .
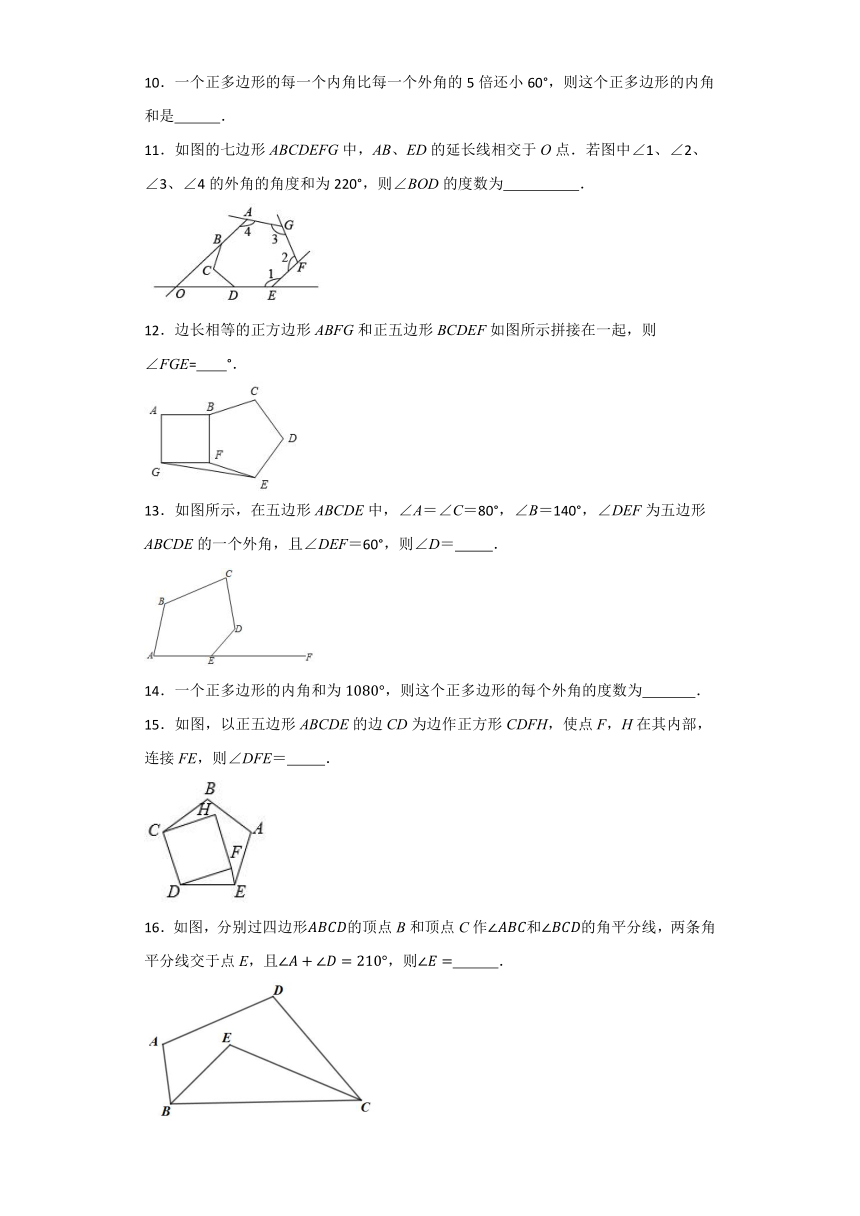
11.如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为 .
12.边长相等的正方边形ABFG和正五边形BCDEF如图所示拼接在一起,则∠FGE= °.
13.如图所示,在五边形ABCDE中,∠A=∠C=80°,∠B=140°,∠DEF为五边形ABCDE的一个外角,且∠DEF=60°,则∠D= .
14.一个正多边形的内角和为,则这个正多边形的每个外角的度数为 .
15.如图,以正五边形ABCDE的边CD为边作正方形CDFH,使点F,H在其内部,连接FE,则∠DFE= .
16.如图,分别过四边形的顶点B和顶点C作和的角平分线,两条角平分线交于点E,且,则 .
三、解答题
17.已知一个正多边形的内角和是,求这个多边形每个外角的度数.
18.在“平面图形的镶嵌”学习中,主要研究了一种或两种正多边形的镶嵌问题,请运用所学知识完成下列问题.
(1)填写表中空格.
正多边形的边数 6 8
正多边形每个内角的度数
(2)根据题意,如果仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)假设在镶嵌的平面图形的一个顶点周围有个正四边形,个正八边形,求和的值,请写出过程.
19.如图,六边形中,,,
(1)求证:.
(2)若,,求.
20.(1)如图1,在四边形中,延长、交于点E,延长、交于点F.当时,我们就称四边形是“完美四边形”.已知在完美四边形中,.
①若,则______°;
②若,则的取值范围是______.
(2)在五边形中,延长任意不相邻的两边(如图2),在相交得到的角中,如果有四个角相等,我们就称这个五边形是“完美五边形”.
如图3,在五边形中,,,该五边形是否为“完美五边形”?请说明你的理由.
21.【感知】如图1所示,在四边形中,分别是边的延长线,我们把称为四边形的外角,若,则___________;
【探究】如图2所示,在四边形中,分别是边的延长线,我们把称为四边形的外角,试探究与之间的数量关系,并说明理由;
【应用】如图3所示,分别是四边形的外角的平分线,若,则的度数为___________.
22.阅读:基本图形通常是指能够反映一个或几个定理,或者能够反映图形基本规律的几何图形.这些图形以基本概念、基本事实、定理、常用的数学结论和基本规律为基础,图形简单又具有代表性.在几何问题中,熟练把握和灵活构造基本图形,能更好地帮助我们解决问题.
我们将图1①所示的图形称为“8字形”.在这个“8字形”中,存在结论.
我们将图1②所示的凹四边形称为“飞镖形”.在这个“飞镖形”中,存在结论.
(1)直接利用上述基本图形中的任意一种,解决问题:
如图2,、分别平分、,说明:.
(2)将图2看作基本图形,直接利用(1)中的结论解决下列问题:
①如图3,直线平分的外角,平分的外角,若,,求的度数.
②在图4中,平分的外角,平分的外角,猜想与、的关系(直接写出结果,无需说明理由).
③在图5中,平分,平分的外角,猜想与、的关系(直接写出结果,无需说明理由).
参考答案
1.解:设所求n边形边数为n,
∵多边形的每个内角均是120°,
∴120n=(n﹣2) 180°,
解得:n=6,
故选:D.
2.解:设所求多边形边数为,
则,
解得,
∴这个多边形的对角线的条数.
故选:D.
3.解:该多边形的外角和为360°,
故内角和为1980°-360°=1620°,
故(n-2) 180°=1620°,
解得n=11.
故选:C.
4.解:①将长方形沿对角线剪开,得到两个三角形,两个多边形的内角和:180°+180°=360°;
②将长方形从一顶点剪向对边,得到一个三角形和一个四边形,两个多边形的内角和为:180°+360°=540°;
③将长方形沿一组对边剪开,得到两个四边形,两个多边形的内角和为:180°+540°=720°,
④将长方形沿一组邻边剪开,得到一个三角形和一个五边形,其内角和为:180°+540°=720°,
故选D.
5.解:A、正五边形每个内角是108°,108°与90°无论怎样也不能组成360°的角,不能密铺,不符合题意;
B、正六边形每个内角是120°,120°与90°无论怎样也不能组成360°的角,不能密铺,不符合题意;
C、正八边形每个内角是135°,135°×2+90°=360°,能密铺,符合题意.
D、正十二边形每个内角是150°,150°与90°无论怎样也不能组成360°的角,不能密铺,不符合题意;
故选:C.
6.解答:
解:∵∠5=90°,
∴∠3+∠4=180° 90°=90°,
∵∠3+∠4+∠1+∠2=360°,
∴∠1+∠2=360° 90°=270°,
故选:C.
7.解:设多边形的边数是.
依题意有,
解得:,
则多边形的边数;
多边形的内角和是;
则未计算的内角的大小为.
故选:C.
8.解:如图,连接,
则,,
,
,
.
故选:D.
9.解:由从某个多边形的一个顶点可以引出3条对角线,可得:
,
∴,
∴这个多边形的内角和为:;
故答案为720°.
10.解:设这个正多边形的外角为x,则内角为5x﹣60°,
由题意得:x+5x﹣60=180,
解得:x=40,
360°÷40°=9.
(9﹣2)×180°=1260°
故答案为:1260°.
11.解:∵∠1、∠2、∠3、∠4的外角的角度和为220°,
∴∠1+∠2+∠3+∠4+220°=4×180°,
∴∠1+∠2+∠3+∠4=500°,
∵五边形OAGFE内角和=(5-2)×180°=540°,
∴∠1+∠2+∠3+∠4+∠BOD=540°,
∴∠BOD=540°-500°=40°,
故答案为:40°.
12.解:∵四边形ABFG是正方形,
∴,
又∵五边形BCDEF是正五边形,
∴正五边形的内角和为,
∴,
∴,
∵,
∴,
∴,
即,
∴;
故答案是9.
13.解:∵∠DEF=60°,
∴∠AED=120°,
∵∠A=∠C=80°,∠B=140°,
∴∠D=180°×(5﹣2)﹣80°﹣80°﹣140°﹣120°=120°,
故答案为:120°.
14.解:设它是n边形,则
(n 2) 180°=1080°,
解得n=8.
360°÷8=45°,
故答案为.
15.解:由正多边形的内角和公式可得:
正五边形ABCDE的内角和为,
∴,
∵四边形CDFH是以CD为边的正方形,
∴,,
∴为等腰三角形,
∴,
故答案为:81°.
16.解:∵,
∴∠ABC+∠BCD=360° ∠A ∠D=150°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=(∠ABC+∠DCB)=75°,
∴∠BEC=180°-75°=105°.
故答案是:105°.
17.解:设正多边形的边数为n,
∵正多边形的内角和为.
∴,
解得:,
∴正多边形的每个外角为:.
18.(1)解:∵正边形的内角为,
∴正五边形的内角为,正六边形的内角为:,正八边形的内角为,
故答案为:;
(2)解:∵仅用一种正多边形镶嵌,
∴,,,,,
∴仅用一种正多边形镶嵌,正三角形,正四边形,正六边形能镶嵌成平面图形;
(3)解:∵有个正四边形,个正八边形,
∴且为正整数,
∴,
∴当时,,满足题意;
当时,,不满足题意;
当时,,不满足题意;
当时,,不满足题意;
∴,,
即的值为,的值为.
19.(1)解:如图,连接,,
∵,,
∴,,
∴,
即;
(2)∵,
∴,
,
∴,
∴,
∵,
∴.
20.解:(1)①∵,,
∴,
,
∴;
故答案为:;
②∵,,
∴,
,
∴,
∵,
∴.
故答案为:.
(2)五边形不是“完美五边形”;理由如下:
延长、交于点F,延长、交于点G,延长、交于点H,延长、交于点K,如图所示:
∵,
∴延长五边形任意不相邻的两边,只能得出4个角,
∴假设五边形为“完美五边形”,
∴,
∴,
∵,,
∴,
∴在中,
在中,
∴,这与矛盾,
∴、、、不可能相等,假设不成立,
∴五边形不是“完美五边形”.
21.解:(感知)四边形的内角和为:,,
,
,,
.
故答案为:.
(探究),理由如下:
,
.
,
.
.
(应用)四边形的内角和为:,,
,
,,
.
.
分别是四边形的外角的平分线,
,,
,
.
故答案为:.
22.(1)解:∵分别平分,
∴,
∴,
由题干的结论得:,∠,
∴,
∴,
∴,即;
(2)解:①如图所示,分作的角平分线交于H,
由(1)的结论可知,
∵分别平分,
∴,
∵
∴,
∴,
同理可得,
由题干的结论可得,
∴;
②如图所示,分作的角平分线交于H,
由(1)的结论可知,,
同理可得,,
∴;
③由题干的结论可得,
∵平分,平分的外角,
∴,
∵,
∴,
由题干的结论可知,
∴,
∴
.
一、单选题
1.若一个多边形的每个内角均是120°,则这个多边形的边数为( )
A.9 B.8 C.7 D.6
2.一个多边形的内角和是,那么这个多边形的对角线的条数是( )
A.2 B.3 C.4 D.5
3.已知一个多边形的内角和与外角和的和为1980°,这个多边形的边数为( )
A.9 B.10 C.11 D.12
4.将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540° C.720° D.730°
5.某中学新科技馆铺设地面,已有正方形地砖,现打算购买另一种正多边形地砖(边长与正方形的相等),与正方形地砖作平面镶嵌,则该学校可以购买的地砖形状是( )
A.正五边形 B.正六边形 C.正八边形 D.正十二边形
6.如图所示,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2的度数为( )
A.135° B.240° C.270° D.300°
7.在计算一个多边形的内角和时,由于粗心少算了1个内角,其和等于1180°,则少算的这个角的度数是( )
A.60 B.70 C.80 D.90
8.如图,( ).
A.180° B.270° C.360° D.540°
二、填空题
9.从某个多边形的一个顶点可以引出3条对角线,则这个多边形内角和的度数为 .
10.一个正多边形的每一个内角比每一个外角的5倍还小60°,则这个正多边形的内角和是 .
11.如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为 .
12.边长相等的正方边形ABFG和正五边形BCDEF如图所示拼接在一起,则∠FGE= °.
13.如图所示,在五边形ABCDE中,∠A=∠C=80°,∠B=140°,∠DEF为五边形ABCDE的一个外角,且∠DEF=60°,则∠D= .
14.一个正多边形的内角和为,则这个正多边形的每个外角的度数为 .
15.如图,以正五边形ABCDE的边CD为边作正方形CDFH,使点F,H在其内部,连接FE,则∠DFE= .
16.如图,分别过四边形的顶点B和顶点C作和的角平分线,两条角平分线交于点E,且,则 .
三、解答题
17.已知一个正多边形的内角和是,求这个多边形每个外角的度数.
18.在“平面图形的镶嵌”学习中,主要研究了一种或两种正多边形的镶嵌问题,请运用所学知识完成下列问题.
(1)填写表中空格.
正多边形的边数 6 8
正多边形每个内角的度数
(2)根据题意,如果仅用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)假设在镶嵌的平面图形的一个顶点周围有个正四边形,个正八边形,求和的值,请写出过程.
19.如图,六边形中,,,
(1)求证:.
(2)若,,求.
20.(1)如图1,在四边形中,延长、交于点E,延长、交于点F.当时,我们就称四边形是“完美四边形”.已知在完美四边形中,.
①若,则______°;
②若,则的取值范围是______.
(2)在五边形中,延长任意不相邻的两边(如图2),在相交得到的角中,如果有四个角相等,我们就称这个五边形是“完美五边形”.
如图3,在五边形中,,,该五边形是否为“完美五边形”?请说明你的理由.
21.【感知】如图1所示,在四边形中,分别是边的延长线,我们把称为四边形的外角,若,则___________;
【探究】如图2所示,在四边形中,分别是边的延长线,我们把称为四边形的外角,试探究与之间的数量关系,并说明理由;
【应用】如图3所示,分别是四边形的外角的平分线,若,则的度数为___________.
22.阅读:基本图形通常是指能够反映一个或几个定理,或者能够反映图形基本规律的几何图形.这些图形以基本概念、基本事实、定理、常用的数学结论和基本规律为基础,图形简单又具有代表性.在几何问题中,熟练把握和灵活构造基本图形,能更好地帮助我们解决问题.
我们将图1①所示的图形称为“8字形”.在这个“8字形”中,存在结论.
我们将图1②所示的凹四边形称为“飞镖形”.在这个“飞镖形”中,存在结论.
(1)直接利用上述基本图形中的任意一种,解决问题:
如图2,、分别平分、,说明:.
(2)将图2看作基本图形,直接利用(1)中的结论解决下列问题:
①如图3,直线平分的外角,平分的外角,若,,求的度数.
②在图4中,平分的外角,平分的外角,猜想与、的关系(直接写出结果,无需说明理由).
③在图5中,平分,平分的外角,猜想与、的关系(直接写出结果,无需说明理由).
参考答案
1.解:设所求n边形边数为n,
∵多边形的每个内角均是120°,
∴120n=(n﹣2) 180°,
解得:n=6,
故选:D.
2.解:设所求多边形边数为,
则,
解得,
∴这个多边形的对角线的条数.
故选:D.
3.解:该多边形的外角和为360°,
故内角和为1980°-360°=1620°,
故(n-2) 180°=1620°,
解得n=11.
故选:C.
4.解:①将长方形沿对角线剪开,得到两个三角形,两个多边形的内角和:180°+180°=360°;
②将长方形从一顶点剪向对边,得到一个三角形和一个四边形,两个多边形的内角和为:180°+360°=540°;
③将长方形沿一组对边剪开,得到两个四边形,两个多边形的内角和为:180°+540°=720°,
④将长方形沿一组邻边剪开,得到一个三角形和一个五边形,其内角和为:180°+540°=720°,
故选D.
5.解:A、正五边形每个内角是108°,108°与90°无论怎样也不能组成360°的角,不能密铺,不符合题意;
B、正六边形每个内角是120°,120°与90°无论怎样也不能组成360°的角,不能密铺,不符合题意;
C、正八边形每个内角是135°,135°×2+90°=360°,能密铺,符合题意.
D、正十二边形每个内角是150°,150°与90°无论怎样也不能组成360°的角,不能密铺,不符合题意;
故选:C.
6.解答:
解:∵∠5=90°,
∴∠3+∠4=180° 90°=90°,
∵∠3+∠4+∠1+∠2=360°,
∴∠1+∠2=360° 90°=270°,
故选:C.
7.解:设多边形的边数是.
依题意有,
解得:,
则多边形的边数;
多边形的内角和是;
则未计算的内角的大小为.
故选:C.
8.解:如图,连接,
则,,
,
,
.
故选:D.
9.解:由从某个多边形的一个顶点可以引出3条对角线,可得:
,
∴,
∴这个多边形的内角和为:;
故答案为720°.
10.解:设这个正多边形的外角为x,则内角为5x﹣60°,
由题意得:x+5x﹣60=180,
解得:x=40,
360°÷40°=9.
(9﹣2)×180°=1260°
故答案为:1260°.
11.解:∵∠1、∠2、∠3、∠4的外角的角度和为220°,
∴∠1+∠2+∠3+∠4+220°=4×180°,
∴∠1+∠2+∠3+∠4=500°,
∵五边形OAGFE内角和=(5-2)×180°=540°,
∴∠1+∠2+∠3+∠4+∠BOD=540°,
∴∠BOD=540°-500°=40°,
故答案为:40°.
12.解:∵四边形ABFG是正方形,
∴,
又∵五边形BCDEF是正五边形,
∴正五边形的内角和为,
∴,
∴,
∵,
∴,
∴,
即,
∴;
故答案是9.
13.解:∵∠DEF=60°,
∴∠AED=120°,
∵∠A=∠C=80°,∠B=140°,
∴∠D=180°×(5﹣2)﹣80°﹣80°﹣140°﹣120°=120°,
故答案为:120°.
14.解:设它是n边形,则
(n 2) 180°=1080°,
解得n=8.
360°÷8=45°,
故答案为.
15.解:由正多边形的内角和公式可得:
正五边形ABCDE的内角和为,
∴,
∵四边形CDFH是以CD为边的正方形,
∴,,
∴为等腰三角形,
∴,
故答案为:81°.
16.解:∵,
∴∠ABC+∠BCD=360° ∠A ∠D=150°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=(∠ABC+∠DCB)=75°,
∴∠BEC=180°-75°=105°.
故答案是:105°.
17.解:设正多边形的边数为n,
∵正多边形的内角和为.
∴,
解得:,
∴正多边形的每个外角为:.
18.(1)解:∵正边形的内角为,
∴正五边形的内角为,正六边形的内角为:,正八边形的内角为,
故答案为:;
(2)解:∵仅用一种正多边形镶嵌,
∴,,,,,
∴仅用一种正多边形镶嵌,正三角形,正四边形,正六边形能镶嵌成平面图形;
(3)解:∵有个正四边形,个正八边形,
∴且为正整数,
∴,
∴当时,,满足题意;
当时,,不满足题意;
当时,,不满足题意;
当时,,不满足题意;
∴,,
即的值为,的值为.
19.(1)解:如图,连接,,
∵,,
∴,,
∴,
即;
(2)∵,
∴,
,
∴,
∴,
∵,
∴.
20.解:(1)①∵,,
∴,
,
∴;
故答案为:;
②∵,,
∴,
,
∴,
∵,
∴.
故答案为:.
(2)五边形不是“完美五边形”;理由如下:
延长、交于点F,延长、交于点G,延长、交于点H,延长、交于点K,如图所示:
∵,
∴延长五边形任意不相邻的两边,只能得出4个角,
∴假设五边形为“完美五边形”,
∴,
∴,
∵,,
∴,
∴在中,
在中,
∴,这与矛盾,
∴、、、不可能相等,假设不成立,
∴五边形不是“完美五边形”.
21.解:(感知)四边形的内角和为:,,
,
,,
.
故答案为:.
(探究),理由如下:
,
.
,
.
.
(应用)四边形的内角和为:,,
,
,,
.
.
分别是四边形的外角的平分线,
,,
,
.
故答案为:.
22.(1)解:∵分别平分,
∴,
∴,
由题干的结论得:,∠,
∴,
∴,
∴,即;
(2)解:①如图所示,分作的角平分线交于H,
由(1)的结论可知,
∵分别平分,
∴,
∵
∴,
∴,
同理可得,
由题干的结论可得,
∴;
②如图所示,分作的角平分线交于H,
由(1)的结论可知,,
同理可得,,
∴;
③由题干的结论可得,
∵平分,平分的外角,
∴,
∵,
∴,
由题干的结论可知,
∴,
∴
.
