2023—2024学年人教版数学八年级上册11.2与三角形有关的角 同步练习题 (含解析)
文档属性
| 名称 | 2023—2024学年人教版数学八年级上册11.2与三角形有关的角 同步练习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 509.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 15:50:19 | ||
图片预览

文档简介
2023-2024学年人教版八年级数学上册《11.2与三角形有关的角》同步练习题(附答案)
一、单选题
1.如图所示,在△ABC中,,,AD是△ABC的角平分线,则∠CAD的度数为( )
A. B. C. D.
2.如果将一副三角板按如图的方式叠放,则的度数为( ).
A.105° B.120° C.75° D.60°
3.如图,一副三角板放在直线上,,,,点,和点在直线上,,则的度数是( )
A. B. C. D.
4.如图,有一个角为30°的直角三角板放置在一个长方形直尺上,若∠1=15°,则∠2为( )
A.110° B.135° C.120° D.145°
5.△ABC中,∠C=50°,∠B=30°,AE平分∠BAC,点F为E上一点,FD⊥DC于点D,则∠EFD=( )
A.5° B.10° C.12° D.20°
6.如图,在△ABC中,,,BP平分∠ABC,CP平分∠ACB,则∠BPC的度数是( )
A. B. C. D.
7.如图,∠BDC=100°,∠C=35°,∠A=28°,则∠B的度数是( )
A.43° B.33° C.47° D.37°
8.如图,将沿着平行于的直线折叠,点落在点处,若,则的度数是( )
A.108° B.104° C.96° D.92°
二、填空题
9.在中,若,,则______
10.Rt△ABC中,,∠ABC和∠CAB的平分线交于点O,则∠BOA=___.
11.如图,是一个风筝的模型,则图中______.
12.如图,中,,,点为边上一点,将沿直线折叠后,点落到点处,,则的度数为______.
13.如图,,BD、BE三等分,CD、CE三等分.那么______.
14.如图,在△ABC中,D,E分别是边AB和BC上的点,若∠B=35°,∠C=56°.∠F=47°,则∠ADF的度数为_____.
15.如图,在中,的内角和外角的角平分线交于点P,已知,则的度数为____________.
16.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,∠ACB=85°,则C处在B处的_____ 度方向.
三、解答题
17.如图所示,已知点A在线段的上方,连接.
(1)过点A作的垂线段,垂足为E;
(2)在(1)的基础上,在所在直线的上方,过点E作;
(3)在(2)的基础上,若,请直接写出的度数.
18.如图,在中,是高,是角平分线,交于点F,,求的度数.
19.已知:如图,是上一点,是上的一点,、相交于点,,,.求:
(1)的度数;
(2)的度数.
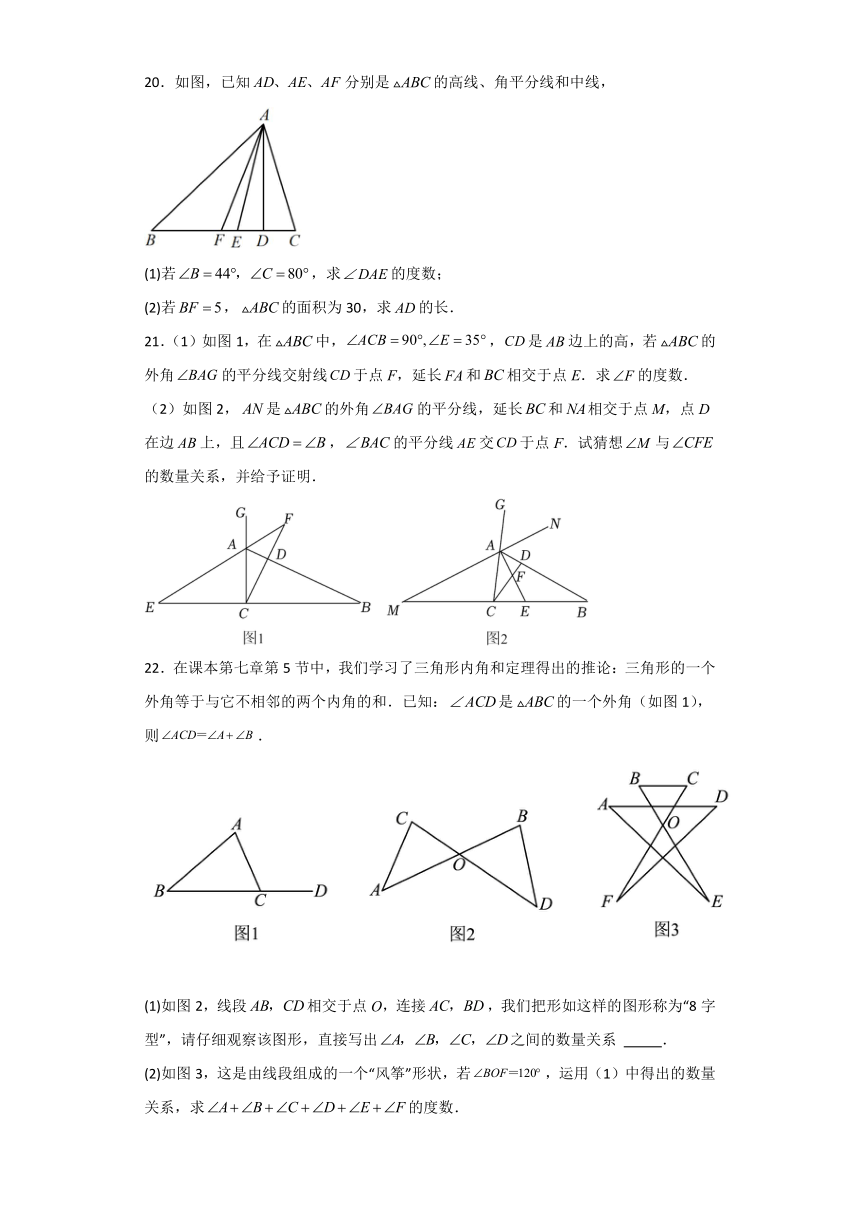
20.如图,已知分别是的高线、角平分线和中线,
(1)若,求的度数;
(2)若,的面积为30,求的长.
21.(1)如图1,在中,,是边上的高,若的外角的平分线交射线于点F,延长和相交于点E.求的度数.
(2)如图2,是的外角的平分线,延长和相交于点M,点D在边上,且,的平分线交于点F.试猜想与的数量关系,并给予证明.
22.在课本第七章第5节中,我们学习了三角形内角和定理得出的推论:三角形的一个外角等于与它不相邻的两个内角的和.已知:是的一个外角(如图1),则.
(1)如图2,线段相交于点O,连接,我们把形如这样的图形称为“8字型”,请仔细观察该图形,直接写出之间的数量关系 .
(2)如图3,这是由线段组成的一个“风筝”形状,若,运用(1)中得出的数量关系,求的度数.
参考答案
1.解:∵,,
∴,
∵AD是△ABC的角平分线,
∴,
故选:D.
2.解:如图,根据三角板的性质可得,
根据三角形外角的性质可得,
故选A
3.解:∵,
∴.
在Rt△DEF中,,
∴,
∴.
故选:B.
4.解:如图,
由题意得:,,
根据三角形内角和得出:,
,
,
为对顶角,
,
故选:B.
5.解:∵∠C=50°,∠B=30°,
∴∠BAC=180°﹣∠C﹣∠A=180°﹣50°﹣30°=100°,
∵AE是∠BAC的平分线,
∴∠BAE=50°,
∴∠FED=50°+30°=80°,
又∵DF⊥BC,
∴∠FED+∠EFD=90°,
∴∠EFD=90°﹣80°=10°,
故选:B.
6.解:∠ABC=50°,∠ACB=80°,
BP平分∠ABC,CP平分∠ACB,
∴∠PBC=25°,∠PCB=40°,
∴∠BPC=180°-25°-40°=115°.
故选:C.
7.解:延长BD交AC于点E,
∵∠BDC=∠C+∠BEC,∠BEC=∠A+∠B,
∴∠BCD=∠A+∠B+∠C,
∵∠BDC=100°,∠A=28°,∠C=35°,
∴∠B=100°-28°-35°=37°,
故选:D.
8.解:∵,
∴∠ADE=∠B=44°,
∵△ABC沿着平行于BC的直线折叠,点A落到点A′,
∴∠A′DE=∠ADE=44°,
∴∠A′DB=180°﹣44°﹣44°=92°.
故选:D.
9.解:∵
∴
故答案为:
10.解:如图,在Rt△ABC中,∠CAB+∠ABC=90°,
∵AO、BO分别是∠CAB与∠ABC的角平分线,
∴∠1=∠CAB,∠2=∠ABC,
∴∠1+∠2=(∠CAB+∠ABC)=×90°=45°,
在△AOB中,∠BOA=180°-(∠1+∠2)=180°-45°=135°.
故答案为:135°.
11.解:延长BC,交AD于点E,如图.
可知∠AEB=∠ECD+∠3,∠4=180°+∠ECD,∠1+∠2+∠AEB=180°,
所以∠1+∠2+∠3+∠ECD=180°.
因为∠ECD=∠4-180°,
所以∠1+∠2+∠3+∠4=360°.
故答案为:360°.
12.解:∵中,,,
∴,
∵,
∴,
由折叠性质可知.
故答案为:40°.
13.解:∵ BD、BE三等分∠ABC
∴∠DBC=∠ABC
又∵CD、CE三等分∠ACB
∴∠DCB=∠ACB
∴∠DBC+∠DCB=(∠ABC+∠ACB)=×(180°-∠A)
∴∠D=180°-× (180°-∠A)=60°+∠A
∵∠A=48°
∴∠D=60°+×48°=92°
故答案为:92°.
14.解:∵∠DAF是△ABC的外角,∠B=35°,∠C=56°.
∴∠DAF=∠B+∠C=91°.
∵∠F=47°,
∴∠ADF=180°-∠F-∠DAF=42°,
故答案为:42°.
15.解:如下图,
AP为∠CAB的角平分线,BP为外角∠CBD的平分线,两角平分线交于点P, ∠CAM=∠BAP=∠BAC,∠PBC=∠PBD=∠CBD,
∠CBD=∠C+∠CAB,
∠PBC=∠PBD=(∠C+2∠PAB) =∠C+∠PAB,
∠PBD=∠PAB+∠P,
∠P=∠C,
,
,
16.解:处在处的南偏西方向,处在处的南偏东方向,
,
,
,
处在处的北偏东,
故答案为80.
17.(1)解:如图,即为所求;
(2)如图,即为所求;
(3)∵,
∴,
∵,
∴,
∵,
∴.
18.解:∵是高线,
∴,
∵,
∴,
∵是角平分线,
∴,
在中,.
19.(1)解:在中,
,,
;
(2)解:在中,.
20.(1)解:∵,
∴,
∴,
∵,
∴,
∴;
(2)解:∵是的中线,
∴,
∴,
∵的面积为30,
∴,即,
∴.
21.解:(1)∵,
∴,
∵为的角平分线,
∴,
∵是边上的高,
∴,
∴;
(2),证明如下:
∵C、A、G三点共线 ,为角平分线,
∴,
∴,
∴,
∵,
∴,
∴.
22.解:(1)∵是的外角,
∴,
∴;
故答案为:;
(2)连接,如图,
由(1)的结论可得:,
,
∵,
∴
,
即,
∴.
一、单选题
1.如图所示,在△ABC中,,,AD是△ABC的角平分线,则∠CAD的度数为( )
A. B. C. D.
2.如果将一副三角板按如图的方式叠放,则的度数为( ).
A.105° B.120° C.75° D.60°
3.如图,一副三角板放在直线上,,,,点,和点在直线上,,则的度数是( )
A. B. C. D.
4.如图,有一个角为30°的直角三角板放置在一个长方形直尺上,若∠1=15°,则∠2为( )
A.110° B.135° C.120° D.145°
5.△ABC中,∠C=50°,∠B=30°,AE平分∠BAC,点F为E上一点,FD⊥DC于点D,则∠EFD=( )
A.5° B.10° C.12° D.20°
6.如图,在△ABC中,,,BP平分∠ABC,CP平分∠ACB,则∠BPC的度数是( )
A. B. C. D.
7.如图,∠BDC=100°,∠C=35°,∠A=28°,则∠B的度数是( )
A.43° B.33° C.47° D.37°
8.如图,将沿着平行于的直线折叠,点落在点处,若,则的度数是( )
A.108° B.104° C.96° D.92°
二、填空题
9.在中,若,,则______
10.Rt△ABC中,,∠ABC和∠CAB的平分线交于点O,则∠BOA=___.
11.如图,是一个风筝的模型,则图中______.
12.如图,中,,,点为边上一点,将沿直线折叠后,点落到点处,,则的度数为______.
13.如图,,BD、BE三等分,CD、CE三等分.那么______.
14.如图,在△ABC中,D,E分别是边AB和BC上的点,若∠B=35°,∠C=56°.∠F=47°,则∠ADF的度数为_____.
15.如图,在中,的内角和外角的角平分线交于点P,已知,则的度数为____________.
16.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,∠ACB=85°,则C处在B处的_____ 度方向.
三、解答题
17.如图所示,已知点A在线段的上方,连接.
(1)过点A作的垂线段,垂足为E;
(2)在(1)的基础上,在所在直线的上方,过点E作;
(3)在(2)的基础上,若,请直接写出的度数.
18.如图,在中,是高,是角平分线,交于点F,,求的度数.
19.已知:如图,是上一点,是上的一点,、相交于点,,,.求:
(1)的度数;
(2)的度数.
20.如图,已知分别是的高线、角平分线和中线,
(1)若,求的度数;
(2)若,的面积为30,求的长.
21.(1)如图1,在中,,是边上的高,若的外角的平分线交射线于点F,延长和相交于点E.求的度数.
(2)如图2,是的外角的平分线,延长和相交于点M,点D在边上,且,的平分线交于点F.试猜想与的数量关系,并给予证明.
22.在课本第七章第5节中,我们学习了三角形内角和定理得出的推论:三角形的一个外角等于与它不相邻的两个内角的和.已知:是的一个外角(如图1),则.
(1)如图2,线段相交于点O,连接,我们把形如这样的图形称为“8字型”,请仔细观察该图形,直接写出之间的数量关系 .
(2)如图3,这是由线段组成的一个“风筝”形状,若,运用(1)中得出的数量关系,求的度数.
参考答案
1.解:∵,,
∴,
∵AD是△ABC的角平分线,
∴,
故选:D.
2.解:如图,根据三角板的性质可得,
根据三角形外角的性质可得,
故选A
3.解:∵,
∴.
在Rt△DEF中,,
∴,
∴.
故选:B.
4.解:如图,
由题意得:,,
根据三角形内角和得出:,
,
,
为对顶角,
,
故选:B.
5.解:∵∠C=50°,∠B=30°,
∴∠BAC=180°﹣∠C﹣∠A=180°﹣50°﹣30°=100°,
∵AE是∠BAC的平分线,
∴∠BAE=50°,
∴∠FED=50°+30°=80°,
又∵DF⊥BC,
∴∠FED+∠EFD=90°,
∴∠EFD=90°﹣80°=10°,
故选:B.
6.解:∠ABC=50°,∠ACB=80°,
BP平分∠ABC,CP平分∠ACB,
∴∠PBC=25°,∠PCB=40°,
∴∠BPC=180°-25°-40°=115°.
故选:C.
7.解:延长BD交AC于点E,
∵∠BDC=∠C+∠BEC,∠BEC=∠A+∠B,
∴∠BCD=∠A+∠B+∠C,
∵∠BDC=100°,∠A=28°,∠C=35°,
∴∠B=100°-28°-35°=37°,
故选:D.
8.解:∵,
∴∠ADE=∠B=44°,
∵△ABC沿着平行于BC的直线折叠,点A落到点A′,
∴∠A′DE=∠ADE=44°,
∴∠A′DB=180°﹣44°﹣44°=92°.
故选:D.
9.解:∵
∴
故答案为:
10.解:如图,在Rt△ABC中,∠CAB+∠ABC=90°,
∵AO、BO分别是∠CAB与∠ABC的角平分线,
∴∠1=∠CAB,∠2=∠ABC,
∴∠1+∠2=(∠CAB+∠ABC)=×90°=45°,
在△AOB中,∠BOA=180°-(∠1+∠2)=180°-45°=135°.
故答案为:135°.
11.解:延长BC,交AD于点E,如图.
可知∠AEB=∠ECD+∠3,∠4=180°+∠ECD,∠1+∠2+∠AEB=180°,
所以∠1+∠2+∠3+∠ECD=180°.
因为∠ECD=∠4-180°,
所以∠1+∠2+∠3+∠4=360°.
故答案为:360°.
12.解:∵中,,,
∴,
∵,
∴,
由折叠性质可知.
故答案为:40°.
13.解:∵ BD、BE三等分∠ABC
∴∠DBC=∠ABC
又∵CD、CE三等分∠ACB
∴∠DCB=∠ACB
∴∠DBC+∠DCB=(∠ABC+∠ACB)=×(180°-∠A)
∴∠D=180°-× (180°-∠A)=60°+∠A
∵∠A=48°
∴∠D=60°+×48°=92°
故答案为:92°.
14.解:∵∠DAF是△ABC的外角,∠B=35°,∠C=56°.
∴∠DAF=∠B+∠C=91°.
∵∠F=47°,
∴∠ADF=180°-∠F-∠DAF=42°,
故答案为:42°.
15.解:如下图,
AP为∠CAB的角平分线,BP为外角∠CBD的平分线,两角平分线交于点P, ∠CAM=∠BAP=∠BAC,∠PBC=∠PBD=∠CBD,
∠CBD=∠C+∠CAB,
∠PBC=∠PBD=(∠C+2∠PAB) =∠C+∠PAB,
∠PBD=∠PAB+∠P,
∠P=∠C,
,
,
16.解:处在处的南偏西方向,处在处的南偏东方向,
,
,
,
处在处的北偏东,
故答案为80.
17.(1)解:如图,即为所求;
(2)如图,即为所求;
(3)∵,
∴,
∵,
∴,
∵,
∴.
18.解:∵是高线,
∴,
∵,
∴,
∵是角平分线,
∴,
在中,.
19.(1)解:在中,
,,
;
(2)解:在中,.
20.(1)解:∵,
∴,
∴,
∵,
∴,
∴;
(2)解:∵是的中线,
∴,
∴,
∵的面积为30,
∴,即,
∴.
21.解:(1)∵,
∴,
∵为的角平分线,
∴,
∵是边上的高,
∴,
∴;
(2),证明如下:
∵C、A、G三点共线 ,为角平分线,
∴,
∴,
∴,
∵,
∴,
∴.
22.解:(1)∵是的外角,
∴,
∴;
故答案为:;
(2)连接,如图,
由(1)的结论可得:,
,
∵,
∴
,
即,
∴.
