12.1全等三角形 同步练习 2023 —2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 12.1全等三角形 同步练习 2023 —2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 166.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 16:06:12 | ||
图片预览

文档简介
12.1全等三角形
一、选择题
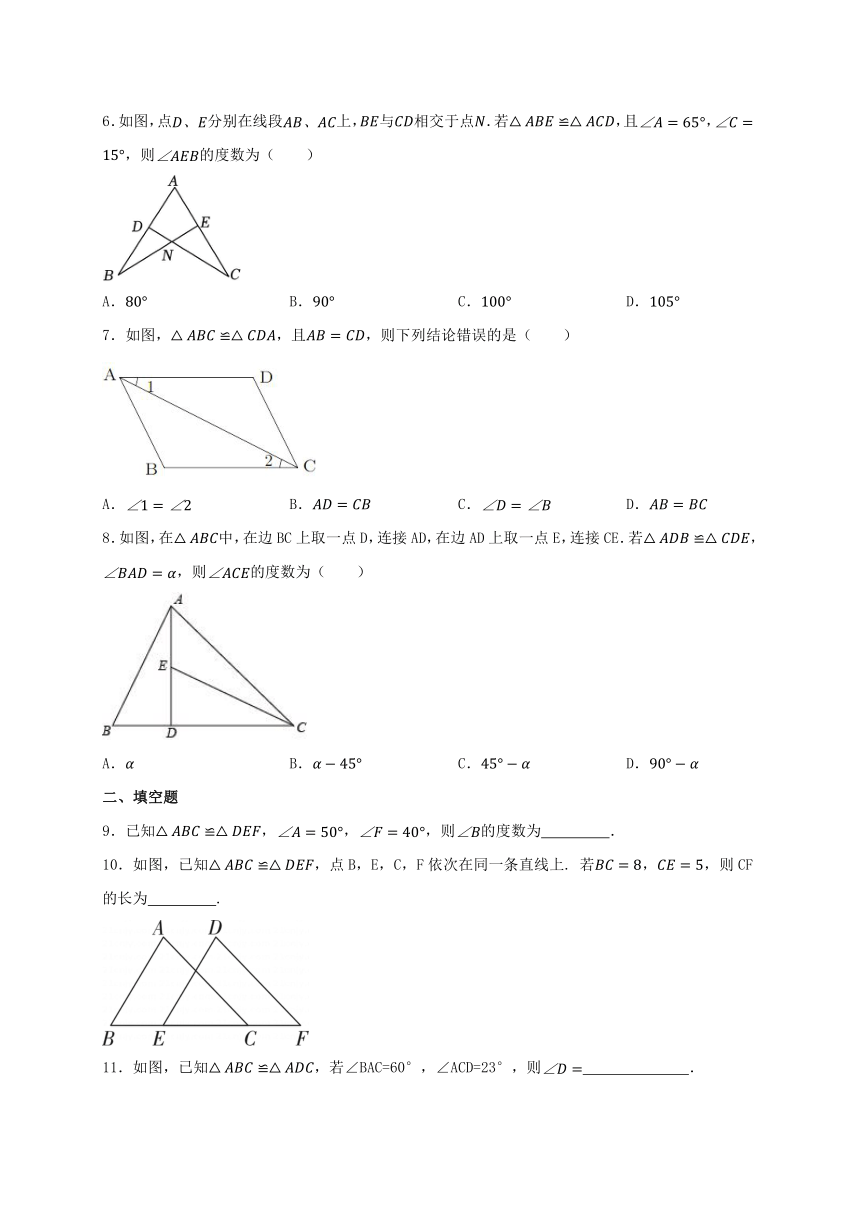
1.下列各项中,两个图形属于全等图形的是( )
A. B.
C. D.
2.下列说法正确的是( )
A.形状相同的两个三角形全等 B.面积相等的两个三角形全等
C.所有的等腰三角形都全等 D.完全重合的两个三角形全等
3.如图,点,,,在同一条直线上,,若,,则的度数为( )
A.50° B.60° C.65° D.120°
4.如图所示的两个三角形全等,则的度数是( )
A. B. C. D.
5.如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=5,DE=2,则CE等于( )
A.2.5 B.3 C.3.5 D.4
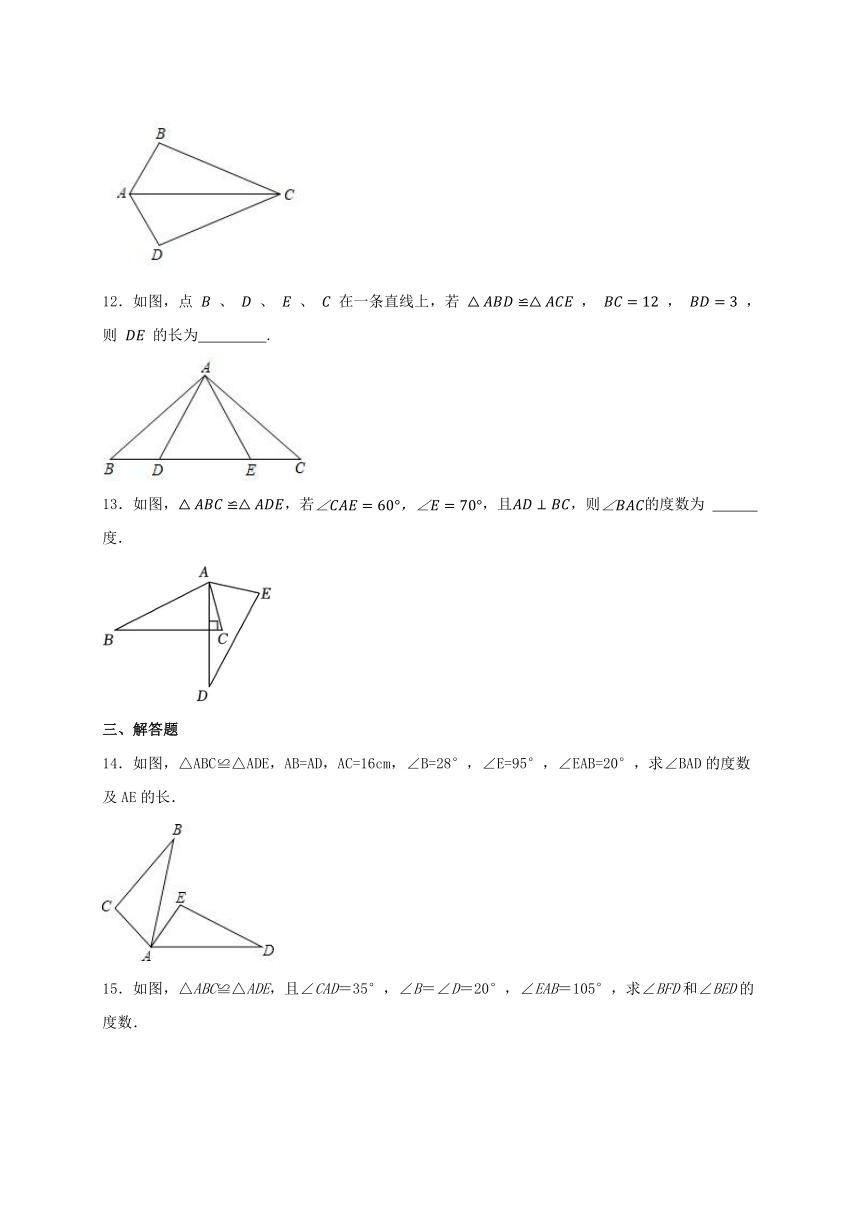
6.如图,点分别在线段上,与相交于点.若,且,,则的度数为( )
A. B. C. D.
7.如图,,且,则下列结论错误的是( )
A. B. C. D.
8.如图,在中,在边BC上取一点D,连接AD,在边AD上取一点E,连接CE.若,,则的度数为( )
A. B. C. D.
二、填空题
9.已知,,,则的度数为 .
10.如图,已知,点B,E,C,F依次在同一条直线上. 若,,则CF的长为 .
11.如图,已知,若∠BAC=60°,∠ACD=23°,则 .
12.如图,点 、 、 、 在一条直线上,若 , , ,则 的长为 .
13.如图,,若,且,则的度数为 度.
三、解答题
14.如图,△ABC≌△ADE,AB=AD,AC=16cm,∠B=28°,∠E=95°,∠EAB=20°,求∠BAD的度数及AE的长.
15.如图,△ABC≌△ADE,且∠CAD=35°,∠B=∠D=20°,∠EAB=105°,求∠BFD和∠BED的度数.
16.如图,已知Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B,C,D三点共线.试说明∠ACE=90°.
17.已知:如图,点E在线段BC上,且△ABC≌△AED.
求证:
(1)∠B=∠AEB;
(2)AE平分∠BED.
18.如图,已知,且点B,C,D在同一条直线上,延长交于点F.
(1)求证:;
(2)已知,,求的长度.
参考答案
1.C
2.D
3.B
4.C
5.B
6.C
7.D
8.C
9.
10.3
11.97°/97度
12.6
13.80
14.解:
∵△ABC≌△ADE,
∴∠D=∠B=28°,AE=AC=16cm,
∵∠E=95°,
∴∠EAD=180°﹣28°﹣95°=57°,
∵∠EAB=20°,
∴∠BAD=∠BAE+∠EAD=20°+57°=77°
15.解:∵ △ABC≌△ADE,
∴∠DAE=∠BAC,
∴∠DAE+∠BAC+∠CAD=105°,
∴2∠BAC=105°-∠CAD=70°,
∴∠BAC=35°,
∴∠BAF=∠BAC+∠CAD=35°+35°=70°,
∴∠BFD=∠B+∠BAF=20°+70°=90°,
∴∠BED=∠BFD-∠D=90°-20°=70°.
16.证明:∵Rt△ABC≌Rt△CDE,
∴∠BCA=∠CED,
∵△DCE是直角三角形,
∴∠CED+∠ECD=90°,
∴∠BCA+∠ECD=90°,
∴∠ACE=180°-90°=90°.
17.(1)证明:∵△ABC≌△AED,
∴AB=AE,
∴∠B=∠AEB;
(2)证明:∵△ABC≌△AED,
∴∠B=∠AED,
又∠B=∠AEB,
∴∠AED=∠AEB,
∴AE平分∠BED.
18.(1)证明:∵,
∴,.
∵点B,C,D在同一条直线上,
∴,
∴.
∵,
∴,
∴,即;
(2)解:∵,
∴,,
∴
∴,
∴.
一、选择题
1.下列各项中,两个图形属于全等图形的是( )
A. B.
C. D.
2.下列说法正确的是( )
A.形状相同的两个三角形全等 B.面积相等的两个三角形全等
C.所有的等腰三角形都全等 D.完全重合的两个三角形全等
3.如图,点,,,在同一条直线上,,若,,则的度数为( )
A.50° B.60° C.65° D.120°
4.如图所示的两个三角形全等,则的度数是( )
A. B. C. D.
5.如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=5,DE=2,则CE等于( )
A.2.5 B.3 C.3.5 D.4
6.如图,点分别在线段上,与相交于点.若,且,,则的度数为( )
A. B. C. D.
7.如图,,且,则下列结论错误的是( )
A. B. C. D.
8.如图,在中,在边BC上取一点D,连接AD,在边AD上取一点E,连接CE.若,,则的度数为( )
A. B. C. D.
二、填空题
9.已知,,,则的度数为 .
10.如图,已知,点B,E,C,F依次在同一条直线上. 若,,则CF的长为 .
11.如图,已知,若∠BAC=60°,∠ACD=23°,则 .
12.如图,点 、 、 、 在一条直线上,若 , , ,则 的长为 .
13.如图,,若,且,则的度数为 度.
三、解答题
14.如图,△ABC≌△ADE,AB=AD,AC=16cm,∠B=28°,∠E=95°,∠EAB=20°,求∠BAD的度数及AE的长.
15.如图,△ABC≌△ADE,且∠CAD=35°,∠B=∠D=20°,∠EAB=105°,求∠BFD和∠BED的度数.
16.如图,已知Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B,C,D三点共线.试说明∠ACE=90°.
17.已知:如图,点E在线段BC上,且△ABC≌△AED.
求证:
(1)∠B=∠AEB;
(2)AE平分∠BED.
18.如图,已知,且点B,C,D在同一条直线上,延长交于点F.
(1)求证:;
(2)已知,,求的长度.
参考答案
1.C
2.D
3.B
4.C
5.B
6.C
7.D
8.C
9.
10.3
11.97°/97度
12.6
13.80
14.解:
∵△ABC≌△ADE,
∴∠D=∠B=28°,AE=AC=16cm,
∵∠E=95°,
∴∠EAD=180°﹣28°﹣95°=57°,
∵∠EAB=20°,
∴∠BAD=∠BAE+∠EAD=20°+57°=77°
15.解:∵ △ABC≌△ADE,
∴∠DAE=∠BAC,
∴∠DAE+∠BAC+∠CAD=105°,
∴2∠BAC=105°-∠CAD=70°,
∴∠BAC=35°,
∴∠BAF=∠BAC+∠CAD=35°+35°=70°,
∴∠BFD=∠B+∠BAF=20°+70°=90°,
∴∠BED=∠BFD-∠D=90°-20°=70°.
16.证明:∵Rt△ABC≌Rt△CDE,
∴∠BCA=∠CED,
∵△DCE是直角三角形,
∴∠CED+∠ECD=90°,
∴∠BCA+∠ECD=90°,
∴∠ACE=180°-90°=90°.
17.(1)证明:∵△ABC≌△AED,
∴AB=AE,
∴∠B=∠AEB;
(2)证明:∵△ABC≌△AED,
∴∠B=∠AED,
又∠B=∠AEB,
∴∠AED=∠AEB,
∴AE平分∠BED.
18.(1)证明:∵,
∴,.
∵点B,C,D在同一条直线上,
∴,
∴.
∵,
∴,
∴,即;
(2)解:∵,
∴,,
∴
∴,
∴.
