11.2与三角形有关的角 同步练习 2023 —2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 11.2与三角形有关的角 同步练习 2023 —2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 153.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-27 16:07:42 | ||
图片预览

文档简介
11.2与三角形有关的角
一、选择题
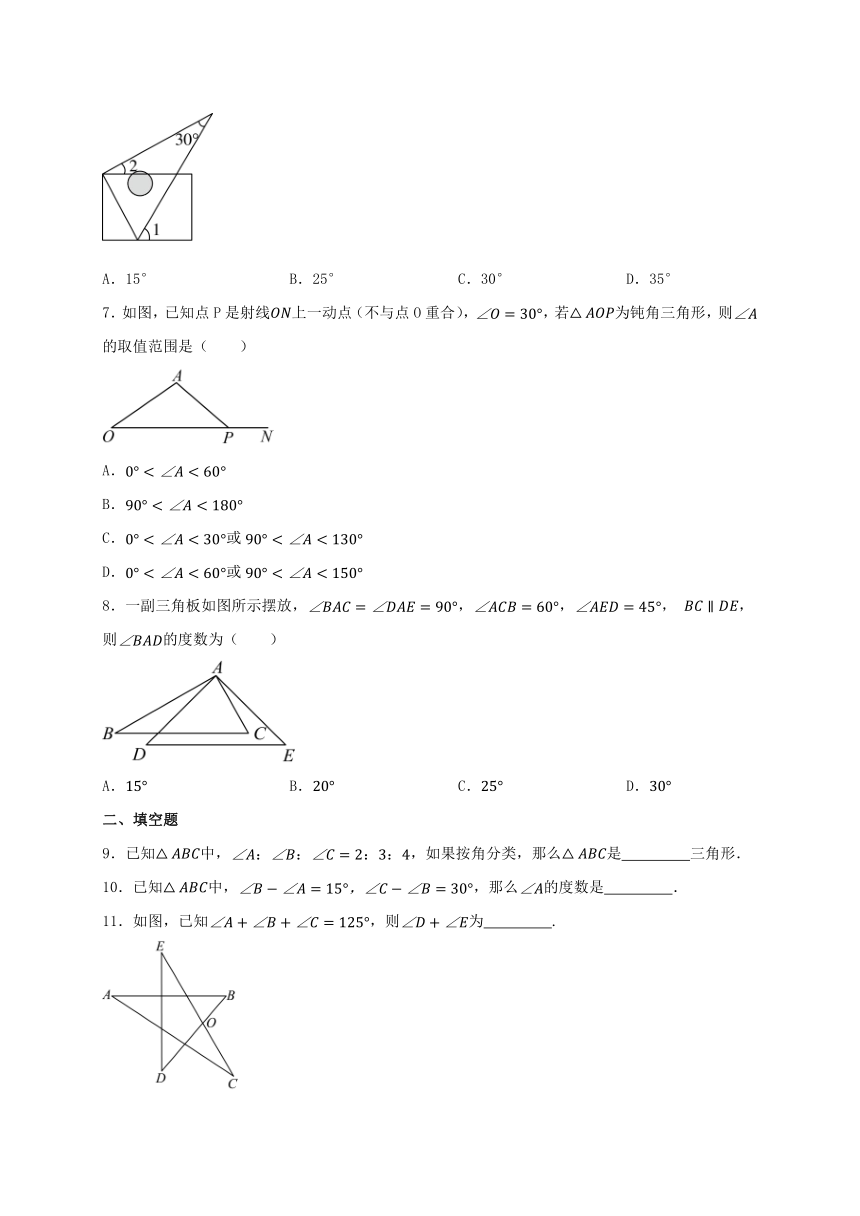
1.如果一个三角形的两个内角分别为和,则这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
2.已知中,,则的角度可能是( )
A. B. C. D.
3.若将一副三角板按如图的方式放置,若,则的度数为( )
A. B. C. D.
4.如图,,含的直角三角板的直角顶点在直线上,若,则的度数为( )
A. B. C. D.
5.如图,一副三角尺按如图所示的方式放置,若,则的度数为( ).
A. B. C. D.
6.如图,将含有30°角的直角三角尺的直角顶点与一张长方形纸片的顶点重合,其中一个锐角顶点在一边上.若,则的度数是( )
A.15° B.25° C.30° D.35°
7.如图,已知点P是射线上一动点(不与点O重合),,若为钝角三角形,则的取值范围是( )
A.
B.
C.或
D.或
8.一副三角板如图所示摆放,,,, ,则的度数为( )
A. B. C. D.
二、填空题
9.已知中,,如果按角分类,那么是 三角形.
10.已知中,,那么的度数是 .
11.如图,已知,则为 .
12.如图,,CE平分,CE与AB交于点F.若,则 .
13.如图,已知,,,那么的度数是 .
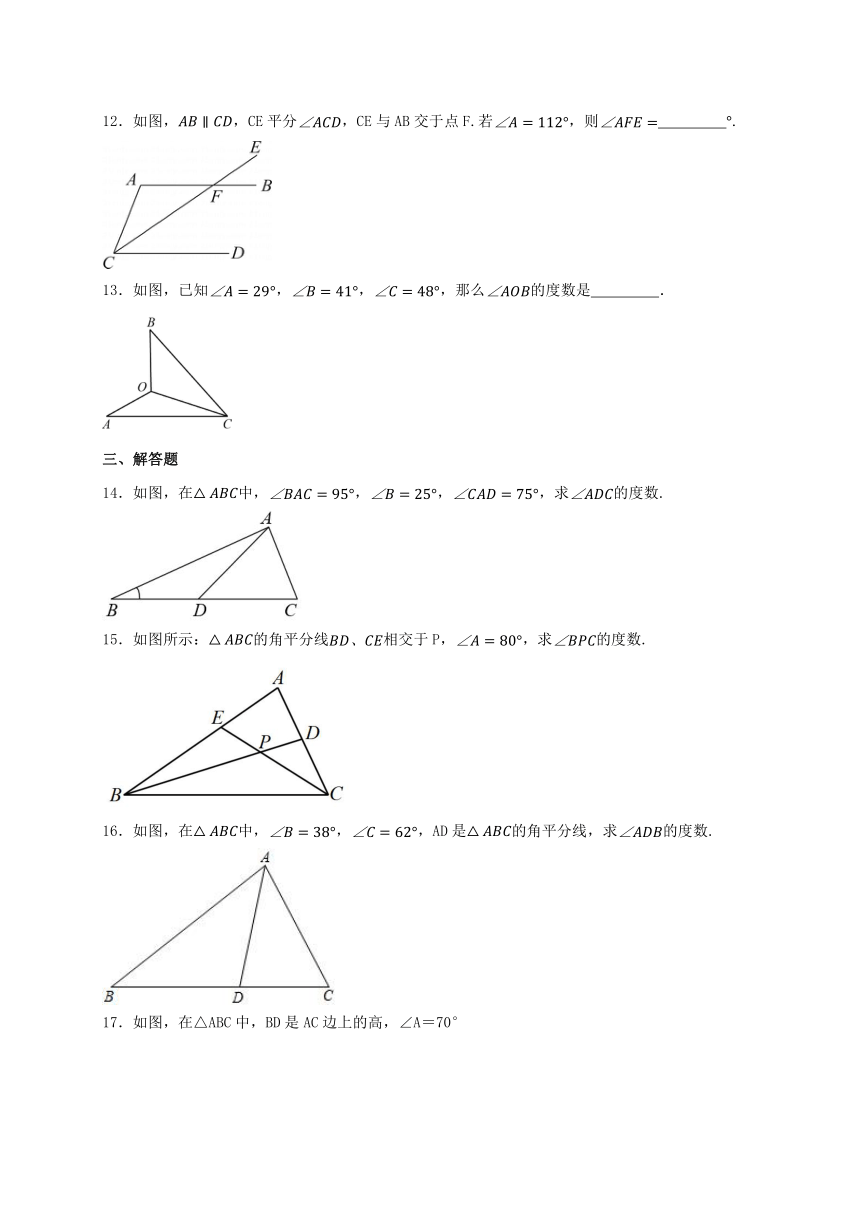
三、解答题
14.如图,在中,,,,求的度数.
15.如图所示:的角平分线相交于P,,求的度数.
16.如图,在中,,,AD是的角平分线,求的度数.
17.如图,在△ABC中,BD是AC边上的高,∠A=70°
(1)求∠ABD;
(2)CE平分∠ACB交BD于点E,∠BEC=118°,求∠ABC.
18.如图,在△ABC中,∠A=30°,点D为△ABC的边AB上一点,过点D作DE⊥AB交AC于点G,过点E作EF∥AC交BC的延长线于点F.
(1)求的度数;
(2)若,求的度数.
参考答案
1.C
2.A
3.B
4.C
5.C
6.B
7.D
8.A
9.锐角
10.
11.
12.146
13.
14.解:∵,,
∴,
∵,
∴.
∴.
15.解:∵的角平分线相交于P,
∴,,
∴,
∵,
∴,
∴,
∴.
16.解:在中,(三角形内角和定理).
∵,(已知),
∴(等式的性质).
∵AD平分(已知),
∴(角平分线的定义).
在中,(三角形内角和定理).
∵(已知),(已证),
∴(等式的性质).
17.(1)解:在中,
是边上的高,
,
,
;
(2)解:在中,
,且,,
,
平分,
,
,
.
18.(1)解:∵DE⊥AB,
∴∠ADE=90°,
∵∠A=30°,
∴∠EGC=∠AGD=180°-90°-30°=60°,
∵,
∴∠E+∠EGC=180°,
∴∠E=180°-∠EGC=180°-60°=120°;
(2)解:∵,
∴∠F+∠ACF=180°,
∵∠F=110°,
∴∠ACF=180°-∠F=180°-110°=70°,
∵∠A=30°,∠A+∠B=∠ACF,
∴∠B=∠ACF-∠A=70°-30°=40°.
一、选择题
1.如果一个三角形的两个内角分别为和,则这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
2.已知中,,则的角度可能是( )
A. B. C. D.
3.若将一副三角板按如图的方式放置,若,则的度数为( )
A. B. C. D.
4.如图,,含的直角三角板的直角顶点在直线上,若,则的度数为( )
A. B. C. D.
5.如图,一副三角尺按如图所示的方式放置,若,则的度数为( ).
A. B. C. D.
6.如图,将含有30°角的直角三角尺的直角顶点与一张长方形纸片的顶点重合,其中一个锐角顶点在一边上.若,则的度数是( )
A.15° B.25° C.30° D.35°
7.如图,已知点P是射线上一动点(不与点O重合),,若为钝角三角形,则的取值范围是( )
A.
B.
C.或
D.或
8.一副三角板如图所示摆放,,,, ,则的度数为( )
A. B. C. D.
二、填空题
9.已知中,,如果按角分类,那么是 三角形.
10.已知中,,那么的度数是 .
11.如图,已知,则为 .
12.如图,,CE平分,CE与AB交于点F.若,则 .
13.如图,已知,,,那么的度数是 .
三、解答题
14.如图,在中,,,,求的度数.
15.如图所示:的角平分线相交于P,,求的度数.
16.如图,在中,,,AD是的角平分线,求的度数.
17.如图,在△ABC中,BD是AC边上的高,∠A=70°
(1)求∠ABD;
(2)CE平分∠ACB交BD于点E,∠BEC=118°,求∠ABC.
18.如图,在△ABC中,∠A=30°,点D为△ABC的边AB上一点,过点D作DE⊥AB交AC于点G,过点E作EF∥AC交BC的延长线于点F.
(1)求的度数;
(2)若,求的度数.
参考答案
1.C
2.A
3.B
4.C
5.C
6.B
7.D
8.A
9.锐角
10.
11.
12.146
13.
14.解:∵,,
∴,
∵,
∴.
∴.
15.解:∵的角平分线相交于P,
∴,,
∴,
∵,
∴,
∴,
∴.
16.解:在中,(三角形内角和定理).
∵,(已知),
∴(等式的性质).
∵AD平分(已知),
∴(角平分线的定义).
在中,(三角形内角和定理).
∵(已知),(已证),
∴(等式的性质).
17.(1)解:在中,
是边上的高,
,
,
;
(2)解:在中,
,且,,
,
平分,
,
,
.
18.(1)解:∵DE⊥AB,
∴∠ADE=90°,
∵∠A=30°,
∴∠EGC=∠AGD=180°-90°-30°=60°,
∵,
∴∠E+∠EGC=180°,
∴∠E=180°-∠EGC=180°-60°=120°;
(2)解:∵,
∴∠F+∠ACF=180°,
∵∠F=110°,
∴∠ACF=180°-∠F=180°-110°=70°,
∵∠A=30°,∠A+∠B=∠ACF,
∴∠B=∠ACF-∠A=70°-30°=40°.
