14.3.1等腰三角形(广东省湛江市霞山区)
文档属性
| 名称 | 14.3.1等腰三角形(广东省湛江市霞山区) |

|
|
| 格式 | rar | ||
| 文件大小 | 188.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-29 00:00:00 | ||
图片预览




文档简介
课件34张PPT。湛江第二十中学 沈海尉14.3.1等腰三角形 对于等腰三角形,你们已经了解了哪些方面的知识?问题 :你知道什么样的三角形是等腰三角形吗?
底边底角底角顶角等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两边相等的三角形叫等腰三角形!
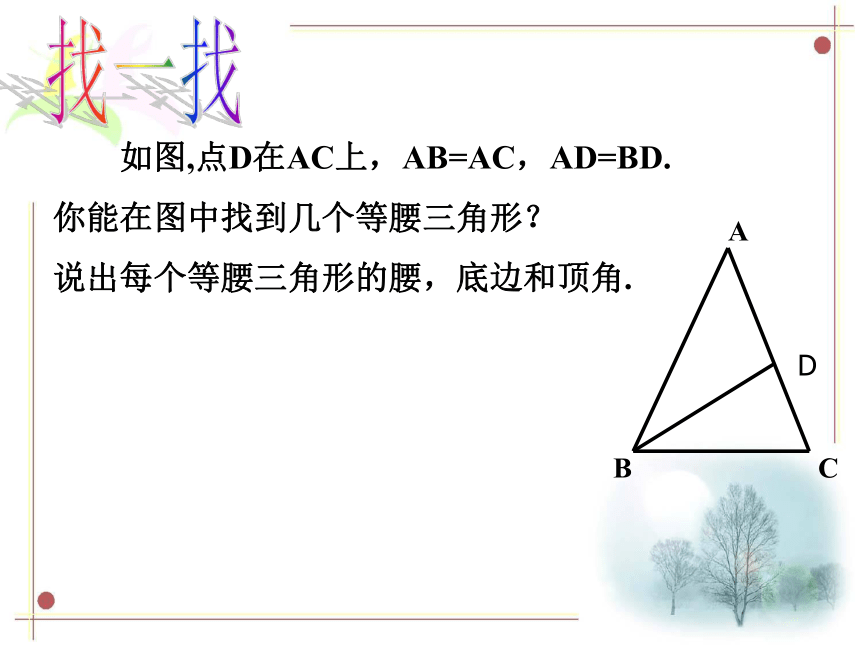
如图,点D在AC上,AB=AC,AD=BD.
你能在图中找到几个等腰三角形?
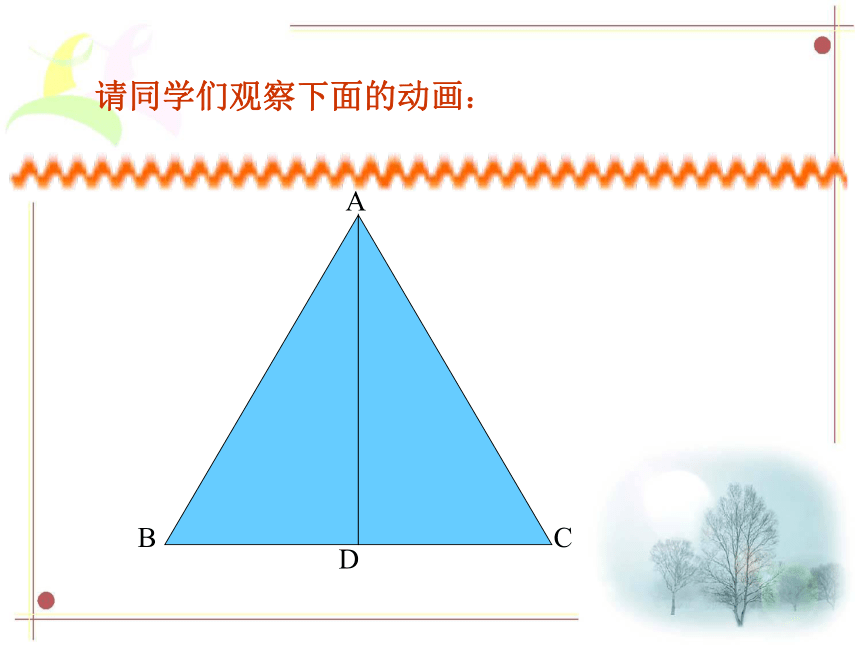
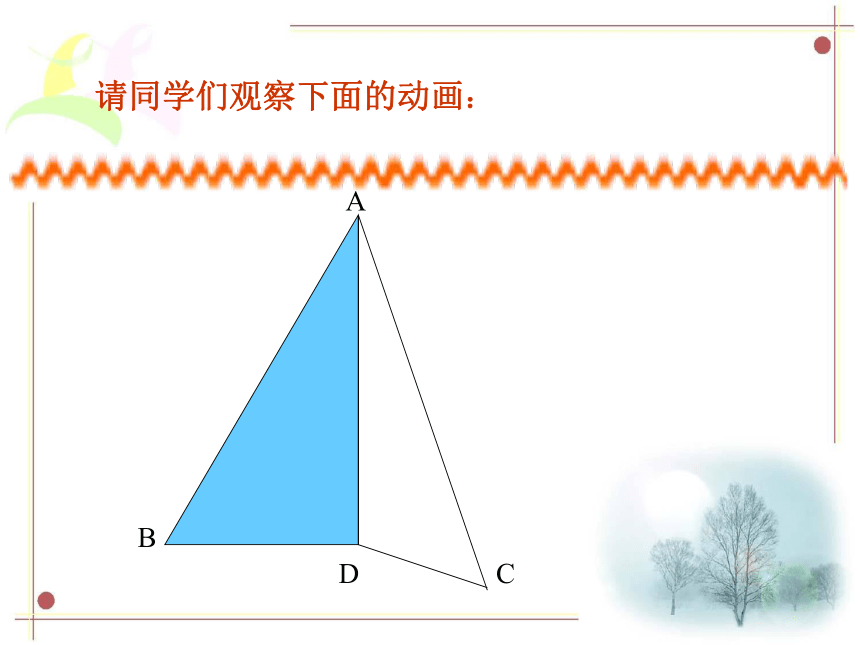
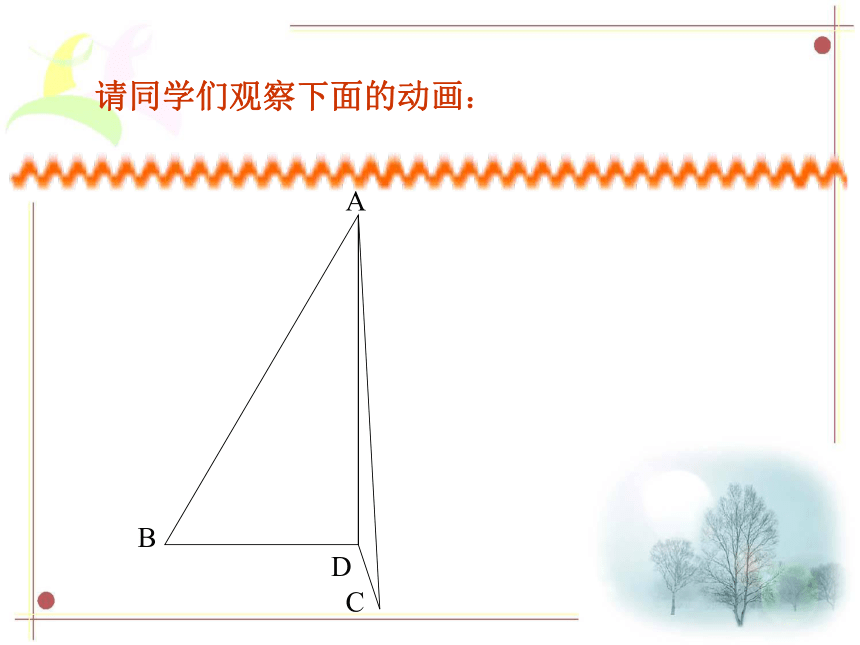
说出每个等腰三角形的腰,底边和顶角.ABCD找一找请同学们观察下面的动画:ACDB请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:请同学们观察下面的动画:C请同学们观察下面的动画:C请同学们观察下面的动画:c请同学们观察下面的动画:c请同学们观察下面的动画:C
能发现什么问题?请同学们观察下面的动画:C请大家尽可能多地写出结论!DBA结论:1、等腰三角形是轴对称图形2、∠ B =∠ C3、BD = CD ,AD 为底边上的中线4、∠ADB = ∠ADC = 90°,AD为底边上的高5、∠BAD = ∠CAD ,AD为顶角平分线等腰三角形的性质:
2.等腰三角形顶角的平分线,底边上的
中线,底边上的高互相重合(三线合一).你能利用已有的公理和定理证明这些结论吗?1 .等腰三角形的两个底角相等 (简写“等边对等角”)在△ABD和 △ACD中
AB=AC (已知)
∠1=∠2(辅助线作法)
AD=AD(公共边) ∴△ABD≌△ACD(SAS) ∴ ∠B=∠C(全等三角形的对应角相等) BD=CD=90 ° 证明:作顶角的平分线AD∠ADB=∠ADC已知: △ABC中 AB=AC试说明 ∠B=∠C的理由等腰三角形的两个底角相等已知:?ABC中 , AB=AC.
求证: ? B=?C.
证明一:作顶角的平分线A D.证明二:作底边的中线AD证明三:作底边的高AD等腰三角形的性质1: 等腰三角形的两个底角相等
(简写成“等边对等角”)注意:
在 三角形中,等边对等角。用符号语言表示为: 在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )已知等边对等角在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 等腰三角形“三线合一”的性质用符号语言表示为:12B DCD12ADBCADBCB DCD 等腰三角形性质的应用: ∠B=∠C∠B=∠C,
BD=CD,∠B=∠C,AD⊥BCAD⊥BC∠1=∠2∠B=∠C,BD=CD,∠1=∠2例1.如图,在△ ABC中, AB = AC
∠ A = 50°
求∠ B , ∠ C的度数解 在△ ABC中∵ AB = AC∴ ∠ B= ∠C∵ ∠A+∠B+∠C=180°,∠A=50° ∴ ∠B=∠C=1/2(180°- ∠A)
= 1/2 (180°- 50°)=65°(等腰三角形的两个底角相等)变式练习1:已知:在△ABC中,AB = AC,
∠A = 50°, 求∠B 和 ∠C的度数。BA变式练习2:已知:等腰三角形的一个内角为 50 °, 求另两个角的度数.例2、已知:在△ABC中,AB = AC,
且BD = BC = AD, 求∠ A的度数。ABCD变式练习:已知等腰三角形的顶角与底角
的比为 4 :1, 求各个内角的度数.练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××作业填空:在△ABC中
(1) ∵ AB=AC ,
∴∠__=∠__
D(2) ∵ AB=AC ,AD是角平分线,
∴ ⊥ , = __.(3) ∵ AB=AC,AD是中线,
∴ ⊥ ,∠_=∠_.(4) ∵ AB=AC,AD 是高,
∴ __ = __,
∠__=∠__. 75°, 30°70°,40°或55°,55°35°,35°文字叙述几何语言等腰三角形的两底角相等(简称等边对等角)∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一)∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD课堂小结思考题已知:如图,AB=AE, ∠B=∠E,BC=ED.
求证: ∠C=∠D再见!授课人:沈海尉2006年11月22日
底边底角底角顶角等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两边相等的三角形叫等腰三角形!
如图,点D在AC上,AB=AC,AD=BD.
你能在图中找到几个等腰三角形?
说出每个等腰三角形的腰,底边和顶角.ABCD找一找请同学们观察下面的动画:ACDB请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:ACBD请同学们观察下面的动画:请同学们观察下面的动画:C请同学们观察下面的动画:C请同学们观察下面的动画:c请同学们观察下面的动画:c请同学们观察下面的动画:C
能发现什么问题?请同学们观察下面的动画:C请大家尽可能多地写出结论!DBA结论:1、等腰三角形是轴对称图形2、∠ B =∠ C3、BD = CD ,AD 为底边上的中线4、∠ADB = ∠ADC = 90°,AD为底边上的高5、∠BAD = ∠CAD ,AD为顶角平分线等腰三角形的性质:
2.等腰三角形顶角的平分线,底边上的
中线,底边上的高互相重合(三线合一).你能利用已有的公理和定理证明这些结论吗?1 .等腰三角形的两个底角相等 (简写“等边对等角”)在△ABD和 △ACD中
AB=AC (已知)
∠1=∠2(辅助线作法)
AD=AD(公共边) ∴△ABD≌△ACD(SAS) ∴ ∠B=∠C(全等三角形的对应角相等) BD=CD=90 ° 证明:作顶角的平分线AD∠ADB=∠ADC已知: △ABC中 AB=AC试说明 ∠B=∠C的理由等腰三角形的两个底角相等已知:?ABC中 , AB=AC.
求证: ? B=?C.
证明一:作顶角的平分线A D.证明二:作底边的中线AD证明三:作底边的高AD等腰三角形的性质1: 等腰三角形的两个底角相等
(简写成“等边对等角”)注意:
在 三角形中,等边对等角。用符号语言表示为: 在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )已知等边对等角在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 等腰三角形“三线合一”的性质用符号语言表示为:12B DCD12ADBCADBCB DCD 等腰三角形性质的应用: ∠B=∠C∠B=∠C,
BD=CD,∠B=∠C,AD⊥BCAD⊥BC∠1=∠2∠B=∠C,BD=CD,∠1=∠2例1.如图,在△ ABC中, AB = AC
∠ A = 50°
求∠ B , ∠ C的度数解 在△ ABC中∵ AB = AC∴ ∠ B= ∠C∵ ∠A+∠B+∠C=180°,∠A=50° ∴ ∠B=∠C=1/2(180°- ∠A)
= 1/2 (180°- 50°)=65°(等腰三角形的两个底角相等)变式练习1:已知:在△ABC中,AB = AC,
∠A = 50°, 求∠B 和 ∠C的度数。BA变式练习2:已知:等腰三角形的一个内角为 50 °, 求另两个角的度数.例2、已知:在△ABC中,AB = AC,
且BD = BC = AD, 求∠ A的度数。ABCD变式练习:已知等腰三角形的顶角与底角
的比为 4 :1, 求各个内角的度数.练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××作业填空:在△ABC中
(1) ∵ AB=AC ,
∴∠__=∠__
D(2) ∵ AB=AC ,AD是角平分线,
∴ ⊥ , = __.(3) ∵ AB=AC,AD是中线,
∴ ⊥ ,∠_=∠_.(4) ∵ AB=AC,AD 是高,
∴ __ = __,
∠__=∠__. 75°, 30°70°,40°或55°,55°35°,35°文字叙述几何语言等腰三角形的两底角相等(简称等边对等角)∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一)∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD课堂小结思考题已知:如图,AB=AE, ∠B=∠E,BC=ED.
求证: ∠C=∠D再见!授课人:沈海尉2006年11月22日
