点和圆,直线和圆的基础练习(无答案)(浙江省台州市玉环县)
文档属性
| 名称 | 点和圆,直线和圆的基础练习(无答案)(浙江省台州市玉环县) |
|
|
| 格式 | rar | ||
| 文件大小 | 52.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-29 00:00:00 | ||
图片预览

文档简介
第二十四章圆的基本性质练习
班级_____________ 学号__________ 姓名_________ 成绩评定________
1、 看准了再选
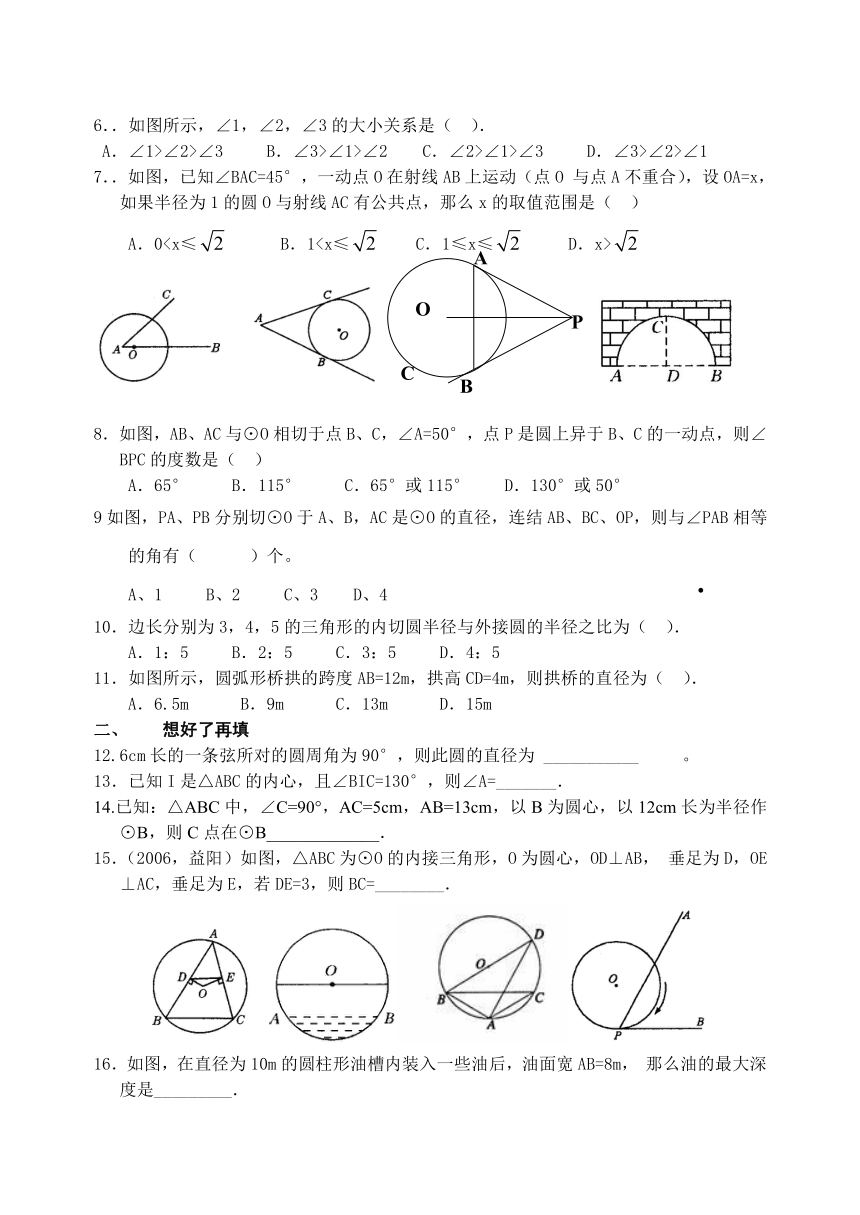
1..如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是( )
A.110° B.70° C.55° D.125°
2.如图,⊙O的直径CD过弦EF的中点G且EF⊥CD,若∠EOD=40°,则∠DCF等于( )
A.80° B. 50° C.40° D. 20°
( http: / / www.czsx. )
3.直线a上有一点到圆心O的距离等于⊙O的半径,则直线a与⊙O的位置关系是( )
A、相离 B、相切 C、相切或相交 D、相交
4.在⊙O中,弦AB垂直并且平分一条半径,则劣弧AB的度数等于( )
A.30° B.120° C.150° D.60°
5.如图,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B,C则BC=( ).
A.3 B.3 C. D.
6..如图所示,∠1,∠2,∠3的大小关系是( ).
A.∠1>∠2>∠3 B.∠3>∠1>∠2 C.∠2>∠1>∠3 D.∠3>∠2>∠1
7..如图,已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的圆O与射线AC有公共点,那么x的取值范围是( )
A.0
( http: / / ) ( http: / / www.czsx. )
8.如图,AB、AC与⊙O相切于点B、C,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是( )
A.65° B.115° C.65°或115° D.130°或50°
9如图,PA、PB分别切⊙O于A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角有( )个。
A、1 B、2 C、3 D、4
10.边长分别为3,4,5的三角形的内切圆半径与外接圆的半径之比为( ).
A.1:5 B.2:5 C.3:5 D.4:5
11.如图所示,圆弧形桥拱的跨度AB=12m,拱高CD=4m,则拱桥的直径为( ).
A.6.5m B.9m C.13m D.15m
2、 想好了再填
12.6cm长的一条弦所对的圆周角为90°,则此圆的直径为 ___________ 。
13.已知I是△ABC的内心,且∠BIC=130°,则∠A=_______.
14.已知:△ABC中,∠C=90°,AC=5cm,AB=13cm,以B为圆心,以12cm长为半径作⊙B,则C点在⊙B_____________.
15.(2006,益阳)如图,△ABC为⊙O的内接三角形,O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=________.
( http: / / www.czsx. ) ( http: / / )
16.如图,在直径为10m的圆柱形油槽内装入一些油后,油面宽AB=8m,那么油的最大深度是_________.
17.(2007山东枣庄)如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为 ⊙O的直径,AD=6,则BC= 。
18.如图所示,∠APB=60°,半径为a的⊙O切PB于P点,若将⊙O在PB上向右滚动,则当滚动到⊙O与PA也相切时,圆心O移动的水平距离是_________.
19.如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,已知AB=8,大圆半径为5,则小圆半径为_______.
20.如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径,则∠A+∠B+∠C=________.
21.若Rt△ABC的内切圆半径为1,斜边长是6,则此三角形的周长为________.
22.如图,PA、PB、DE分别切⊙O于A、B、C,若⊙O的半径为6cm,PO=10cm,则△PDE的周长为___________
23.(2007重庆市)已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=450。给出以下五个结论:①∠EBC=22.50,;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC。其中正确结论的序号是 。
三.想好了再规范的写画
24.如图所示,线段AD过圆心O交⊙O于D,C两点,∠EOD=78°,AE交⊙O于B, 且AB=OC,求∠A的度数.
( http: / / www.czsx. )
25.如图AB是⊙O的直径,AC是弦,OD⊥AB于O,交AC于D,OD=2,∠A=30°,求CD。
26.如图,已知在Rt△ABC中,AC=12,BC=9,D是AB上一点,以O为圆心,BD为直径的⊙O切AC于E,求AD的长。
27.如图所示,AB是⊙O的直径,AB=AC,D,E在⊙O上,说明BD=DE
28.如图,AB是⊙O的直径,CO⊥AB于O,连CB交⊙O于D,过D作⊙O的切线EF交CO于E,求证:CE=DE
29.如图,AD是△ABC的外接圆的⊙O的直径,AD=10㎝,∠DAC=∠ABC,求AC的长。
30.如图所示,某地有一座圆弧形的拱桥,桥下的水平宽度为7.2m,拱顶高出水面2.4m,现有一艘宽为3m,船舱顶部为长方形,并高出水面2m的货船要经过这里,此货船能顺利通过这座拱桥吗?用你所学的数学知识说明理由.
( http: / / www.czsx. )
31.如图所示,AB,AC是⊙O的弦,AD⊥BC于D,交⊙O于F,AE与⊙O的直径,试问两弦BE与CF的大小有何关系,说明理由.
( http: / / www.czsx. )
A
P
B
C
O
A
B
D
C
O
E
P
·
B
A
C
D
O
C
E
A
D
O
B
C
E
D
F
B
O
A
B
O
D
C
班级_____________ 学号__________ 姓名_________ 成绩评定________
1、 看准了再选
1..如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是( )
A.110° B.70° C.55° D.125°
2.如图,⊙O的直径CD过弦EF的中点G且EF⊥CD,若∠EOD=40°,则∠DCF等于( )
A.80° B. 50° C.40° D. 20°
( http: / / www.czsx. )
3.直线a上有一点到圆心O的距离等于⊙O的半径,则直线a与⊙O的位置关系是( )
A、相离 B、相切 C、相切或相交 D、相交
4.在⊙O中,弦AB垂直并且平分一条半径,则劣弧AB的度数等于( )
A.30° B.120° C.150° D.60°
5.如图,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B,C则BC=( ).
A.3 B.3 C. D.
6..如图所示,∠1,∠2,∠3的大小关系是( ).
A.∠1>∠2>∠3 B.∠3>∠1>∠2 C.∠2>∠1>∠3 D.∠3>∠2>∠1
7..如图,已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的圆O与射线AC有公共点,那么x的取值范围是( )
A.0
( http: / / ) ( http: / / www.czsx. )
8.如图,AB、AC与⊙O相切于点B、C,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是( )
A.65° B.115° C.65°或115° D.130°或50°
9如图,PA、PB分别切⊙O于A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角有( )个。
A、1 B、2 C、3 D、4
10.边长分别为3,4,5的三角形的内切圆半径与外接圆的半径之比为( ).
A.1:5 B.2:5 C.3:5 D.4:5
11.如图所示,圆弧形桥拱的跨度AB=12m,拱高CD=4m,则拱桥的直径为( ).
A.6.5m B.9m C.13m D.15m
2、 想好了再填
12.6cm长的一条弦所对的圆周角为90°,则此圆的直径为 ___________ 。
13.已知I是△ABC的内心,且∠BIC=130°,则∠A=_______.
14.已知:△ABC中,∠C=90°,AC=5cm,AB=13cm,以B为圆心,以12cm长为半径作⊙B,则C点在⊙B_____________.
15.(2006,益阳)如图,△ABC为⊙O的内接三角形,O为圆心,OD⊥AB,垂足为D,OE⊥AC,垂足为E,若DE=3,则BC=________.
( http: / / www.czsx. ) ( http: / / )
16.如图,在直径为10m的圆柱形油槽内装入一些油后,油面宽AB=8m,那么油的最大深度是_________.
17.(2007山东枣庄)如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为 ⊙O的直径,AD=6,则BC= 。
18.如图所示,∠APB=60°,半径为a的⊙O切PB于P点,若将⊙O在PB上向右滚动,则当滚动到⊙O与PA也相切时,圆心O移动的水平距离是_________.
19.如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,已知AB=8,大圆半径为5,则小圆半径为_______.
20.如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径,则∠A+∠B+∠C=________.
21.若Rt△ABC的内切圆半径为1,斜边长是6,则此三角形的周长为________.
22.如图,PA、PB、DE分别切⊙O于A、B、C,若⊙O的半径为6cm,PO=10cm,则△PDE的周长为___________
23.(2007重庆市)已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=450。给出以下五个结论:①∠EBC=22.50,;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC。其中正确结论的序号是 。
三.想好了再规范的写画
24.如图所示,线段AD过圆心O交⊙O于D,C两点,∠EOD=78°,AE交⊙O于B, 且AB=OC,求∠A的度数.
( http: / / www.czsx. )
25.如图AB是⊙O的直径,AC是弦,OD⊥AB于O,交AC于D,OD=2,∠A=30°,求CD。
26.如图,已知在Rt△ABC中,AC=12,BC=9,D是AB上一点,以O为圆心,BD为直径的⊙O切AC于E,求AD的长。
27.如图所示,AB是⊙O的直径,AB=AC,D,E在⊙O上,说明BD=DE
28.如图,AB是⊙O的直径,CO⊥AB于O,连CB交⊙O于D,过D作⊙O的切线EF交CO于E,求证:CE=DE
29.如图,AD是△ABC的外接圆的⊙O的直径,AD=10㎝,∠DAC=∠ABC,求AC的长。
30.如图所示,某地有一座圆弧形的拱桥,桥下的水平宽度为7.2m,拱顶高出水面2.4m,现有一艘宽为3m,船舱顶部为长方形,并高出水面2m的货船要经过这里,此货船能顺利通过这座拱桥吗?用你所学的数学知识说明理由.
( http: / / www.czsx. )
31.如图所示,AB,AC是⊙O的弦,AD⊥BC于D,交⊙O于F,AE与⊙O的直径,试问两弦BE与CF的大小有何关系,说明理由.
( http: / / www.czsx. )
A
P
B
C
O
A
B
D
C
O
E
P
·
B
A
C
D
O
C
E
A
D
O
B
C
E
D
F
B
O
A
B
O
D
C
同课章节目录
