4.4 实验:用双缝干涉测量光的波长 同步练(含答案) 高中物理人教版(2019)选择性 必修 第一册
文档属性
| 名称 | 4.4 实验:用双缝干涉测量光的波长 同步练(含答案) 高中物理人教版(2019)选择性 必修 第一册 | 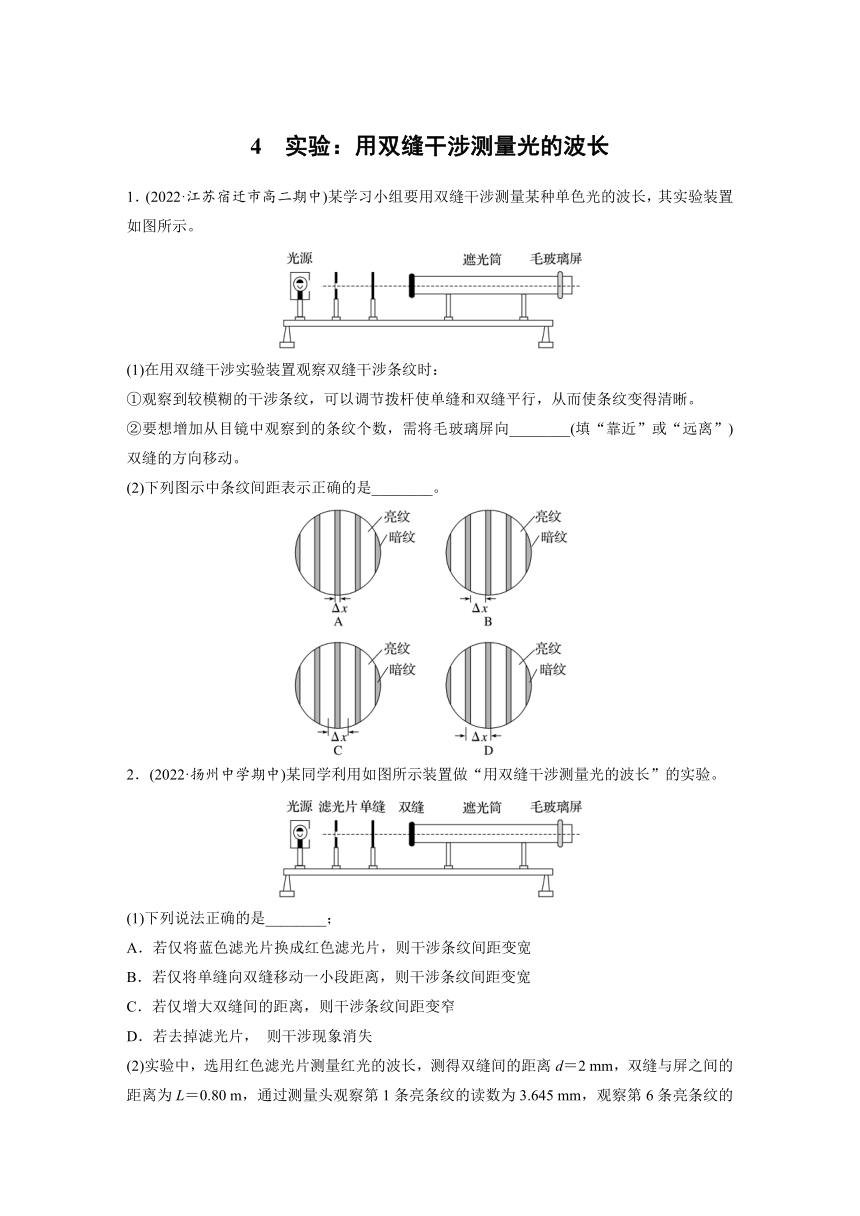 | |
| 格式 | docx | ||
| 文件大小 | 346.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-27 13:46:14 | ||
图片预览



文档简介
4 实验:用双缝干涉测量光的波长
1.(2022·江苏宿迁市高二期中)某学习小组要用双缝干涉测量某种单色光的波长,其实验装置如图所示。
(1)在用双缝干涉实验装置观察双缝干涉条纹时:
①观察到较模糊的干涉条纹,可以调节拨杆使单缝和双缝平行,从而使条纹变得清晰。
②要想增加从目镜中观察到的条纹个数,需将毛玻璃屏向________(填“靠近”或“远离”)双缝的方向移动。
(2)下列图示中条纹间距表示正确的是________。
2.(2022·扬州中学期中)某同学利用如图所示装置做“用双缝干涉测量光的波长”的实验。
(1)下列说法正确的是________;
A.若仅将蓝色滤光片换成红色滤光片,则干涉条纹间距变宽
B.若仅将单缝向双缝移动一小段距离,则干涉条纹间距变宽
C.若仅增大双缝间的距离,则干涉条纹间距变窄
D.若去掉滤光片, 则干涉现象消失
(2)实验中,选用红色滤光片测量红光的波长,测得双缝间的距离d=2 mm,双缝与屏之间的距离为L=0.80 m,通过测量头观察第1条亮条纹的读数为3.645 mm,观察第6条亮条纹的读数为4.945 mm。由此求得红光的波长为________ m(计算结果保留三位有效数字)。
3.在“用双缝干涉测量光的波长”的实验中,将所用器材按要求安装在如图所示的光具座上,然后接通电源使光源正常工作。
(1)某同学调节完实验装置并观察了实验现象后,总结出以下几点,你认为正确的是________。
A.干涉条纹与双缝垂直
B.干涉条纹的疏密程度与单缝宽度有关
C.干涉条纹的疏密程度与光的波长有关
(2)若双缝的间距为d,屏与双缝间的距离为l,测得第2条亮条纹中心与第6条亮条纹中心之间的距离为x,则该单色光的波长λ=________。
4.(2022·江苏泰州市高二期末)如图甲所示是利用双缝干涉测量光的波长的实验装置。
(1)图甲中,单缝和双缝的空间关系应该为相互________(选填“垂直”或“平行”)放置。
(2)测量时,分划板中心刻线对齐某一条亮条纹的中心时游标卡尺的示数如图乙所示,则读数为________ cm。
(3)双缝干涉实验装置的截面图如图丙。单缝S到S1、S2的距离相等,O点为S1、S2连线中垂线与光屏的交点。光源发出的光在真空中的波长为λ,经单缝S后,在经S1出射后垂直穿过玻璃片传播到O点,经S2出射后直接传播到O点。现在已知玻璃片的厚度为d,玻璃对该光的折射率为1.5,真空中的光速为c,不计光在玻璃片内、外的反射。下列判断正确的是________。
A.若玻璃片的厚度d=15λ,则O点处为亮条纹
B.若单缝S略微向左移动(经S1出射后仍可垂直穿过玻璃片),则原O点位置处的条纹位置不变
C.若单缝S略微向下移动(经S出射后仍可垂直穿过玻璃片),则原O点位置处的条纹也略微向下移动
D.若用该波长的光完成实验,O点处为亮条纹,保持其他条件不变的情况下,用另一种波长的光实验,O点处也一定为亮条纹
5.(2023·浙江杭州市长征中学期中)用普通小灯泡作为光源完成“用双缝干涉测量光的波长”实验,首先将实验仪器按图甲所示的方式安装在光具座上。
(1)下列做法,有助于减小实验误差的是______;
A.将单缝拆下
B.将单缝与双缝的位置互换
C.增大单缝与双缝间的距离
D.一次测出多条亮条纹间的距离,再算出相邻亮条纹的间距
(2)某同学选用红色滤光片进行测量,使测量头分划板中心刻线与某一亮条纹A的中心对齐,此时测量头上的游标卡尺如图乙所示(图乙为50分度游标卡尺),其读数x1=________ mm。然后转动手轮,使分划板中心刻线与另一亮条纹B的中心对齐,此时游标卡尺的读数为x2(x2>x1),已知亮条纹A、B间还有4条亮条纹,则相邻亮条纹的间距为________(用x1和x2表示);
(3)若相邻亮条纹的间距记为Δx,双缝间距、屏与双缝间的距离分别记为d和l,则测量得到的单色光波长λ=________(用Δx、d和l表示)。
6.洛埃德在1834年提出了一种更简单的观察干涉的装置。如图所示,单色光从单缝S射出,一部分入射到平面镜后反射到光屏上,另一部分直接投射到屏上,在屏上两光束交叠区域里将出现干涉条纹。单缝S通过平面镜成的像是S′。
(1)通过洛埃德镜在屏上可以观察到明暗相间的干涉条纹,这和双缝干涉实验得到的干涉条纹一致。如果S被视为其中的一个缝,________相当于另一个“缝”;
(2)实验中已知单缝S到平面镜的垂直距离h=0.15 mm,单缝到光屏的距离D=1.2 m,观测到第3个亮条纹中心到第12个亮条纹中心的间距为22.78 mm,则该单色光的波长λ=________ m(结果保留3位有效数字);
(3)下列能够增大光屏上相邻两条亮纹之间的距离的操作是________;
A.将平面镜稍向上移动一些
B.将平面镜稍向右移动一些
C.将光源由红色光改为绿色光
(4)实验表明,光从光疏介质射向光密介质界面发生反射,在入射角接近90°时,反射光与入射光相比,相位有π的变化,称为“半波损失”。如果把光屏移动到和平面镜接触,接触点P处是________。(选填“亮条纹”或“暗条纹”)
4 实验:用双缝干涉测量光的波长
1.(1)②靠近 (2)C
解析 (1)②若增加从目镜中观察到的条纹个数,则条纹间距应减小,根据Δx=λ可知需将毛玻璃屏向靠近双缝的方向移动。
(2)条纹间距指的是相邻两条亮条纹的中心线间的距离或者相邻两条暗条纹的中心线间的距离,故选C。
2.(1)AC (2)6.50×10-7
解析 (1)相邻两亮条纹间距Δx=λ,蓝光波长小于红光波长,将蓝色滤光片换成红色滤光片,则干涉条纹间距变宽,故A正确;条纹间距与单缝和双缝间的距离无关,故B错误;双缝间距变大,条纹间距变小,故C正确;光源发出的光如果不是单色光,去掉滤光片,仍能发生干涉现象,是复色光的干涉,故D错误。
(2)条纹间距Δx==0.26 mm
双缝与屏之间的距离为L=0.80 m,双缝间的距离d=2 mm,
由Δx=λ得λ=,
代入数据得λ=6.50×10-7 m。
3.(1)C (2)
解析 (1)实验中所得到的干涉条纹与双缝平行,故A错误;由Δx=λ可知,干涉条件的疏密程度与双缝间的距离、双缝到屏的距离以及光的波长有关,故C正确,B错误。
(2)由题意可知,相邻亮条纹间的距离为Δx=,又Δx=λ,解得λ=。
4.(1)平行 (2)1.05 (3)B
解析 (1)只有保证单缝和双缝互相平行,才能在屏上出现明暗相间的条纹。
(2)游标尺为10分度,主尺读数为10 mm,游标尺上第5条刻度线与主尺上的刻度线对齐,故读数为10 mm+5×0.1 mm=10.5 mm=1.05 cm。
(3)光在玻璃中传播时对应的路程为l′=c·=nd,S1、S2到O点的路程差为Δl=l′-d=nd-d=λ,
可知,S1、S2到O点的路程差为半波长的奇数倍,故O点处为暗条纹,故A错误;
单缝向左移动,改变了单缝到双缝的距离,不会影响光经过双缝后的传播情况,故屏上的条纹分布情况不变,故B正确;
若单缝S略微向下移动,则主光轴逆时针倾斜,则原O点位置处的条纹略微向上移动,故C错误;
O点处为亮条纹或暗条纹,与玻璃片的厚度,光的波长都有关系,所以用该波长的光完成实验,O点处为亮条纹,保持其他条件不变的情况下,用另一种波长的光实验,O点处可能为亮条纹,也可能为暗条纹,故D错误。
5.(1)D (2)10.36 (3)Δx
解析 (1)将单缝拆下或将单缝与双缝的位置互换,则无法获得干涉图样,实验无法完成,故A、B错误;增大单缝与双缝间的距离,对实验结果没有影响,故C错误;一次测出多条亮条纹间的距离,再算出相邻亮条纹的间距,这样有助于减小实验误差,故D正确。
(2)由题图乙知,50分度游标卡尺的读数为x1=(10+18×0.02) mm=10.36 mm;已知亮条纹A、B间还有4条亮条纹,则相邻亮条纹的间距为Δx=。
(3)由干涉条纹的间距公式Δx=λ知,测量得到的单色光波长λ=Δx。
6.(1)S′ (2)6.33×10-7 (3)A (4)暗条纹
解析 (1)通过洛埃德镜在屏上可以观察到明暗相间的干涉条纹,这和双缝干涉实验得到的干涉条纹一致。如果S被视为其中的一个缝,S′相当于另一个“缝”。
(2)第3个亮条纹中心到第12个亮条纹中心的间距为22.78 mm,
则相邻亮条纹间距为Δx= m≈2.53×10-3 m
等效双缝间的距离为d=2h=0.30 mm=3.0×10-4 m
根据双缝干涉条纹间距公式有Δx=λ
则有λ== m≈6.33×10-7 m。
(3)根据Δx=λ可知,仅增大D,仅减小d,仅增大波长λ,能够增大光屏上相邻两条亮条纹之间的距离,所以A正确,B、C错误。
(4)如果把光屏移动到和平面镜接触,在入射角接近90°时,反射光与入射光相比,相位有π的变化,即“半波损失”,故直接射到光屏上的光和经平面镜反射的光相位差为π,所以接触点P处是暗条纹。
1.(2022·江苏宿迁市高二期中)某学习小组要用双缝干涉测量某种单色光的波长,其实验装置如图所示。
(1)在用双缝干涉实验装置观察双缝干涉条纹时:
①观察到较模糊的干涉条纹,可以调节拨杆使单缝和双缝平行,从而使条纹变得清晰。
②要想增加从目镜中观察到的条纹个数,需将毛玻璃屏向________(填“靠近”或“远离”)双缝的方向移动。
(2)下列图示中条纹间距表示正确的是________。
2.(2022·扬州中学期中)某同学利用如图所示装置做“用双缝干涉测量光的波长”的实验。
(1)下列说法正确的是________;
A.若仅将蓝色滤光片换成红色滤光片,则干涉条纹间距变宽
B.若仅将单缝向双缝移动一小段距离,则干涉条纹间距变宽
C.若仅增大双缝间的距离,则干涉条纹间距变窄
D.若去掉滤光片, 则干涉现象消失
(2)实验中,选用红色滤光片测量红光的波长,测得双缝间的距离d=2 mm,双缝与屏之间的距离为L=0.80 m,通过测量头观察第1条亮条纹的读数为3.645 mm,观察第6条亮条纹的读数为4.945 mm。由此求得红光的波长为________ m(计算结果保留三位有效数字)。
3.在“用双缝干涉测量光的波长”的实验中,将所用器材按要求安装在如图所示的光具座上,然后接通电源使光源正常工作。
(1)某同学调节完实验装置并观察了实验现象后,总结出以下几点,你认为正确的是________。
A.干涉条纹与双缝垂直
B.干涉条纹的疏密程度与单缝宽度有关
C.干涉条纹的疏密程度与光的波长有关
(2)若双缝的间距为d,屏与双缝间的距离为l,测得第2条亮条纹中心与第6条亮条纹中心之间的距离为x,则该单色光的波长λ=________。
4.(2022·江苏泰州市高二期末)如图甲所示是利用双缝干涉测量光的波长的实验装置。
(1)图甲中,单缝和双缝的空间关系应该为相互________(选填“垂直”或“平行”)放置。
(2)测量时,分划板中心刻线对齐某一条亮条纹的中心时游标卡尺的示数如图乙所示,则读数为________ cm。
(3)双缝干涉实验装置的截面图如图丙。单缝S到S1、S2的距离相等,O点为S1、S2连线中垂线与光屏的交点。光源发出的光在真空中的波长为λ,经单缝S后,在经S1出射后垂直穿过玻璃片传播到O点,经S2出射后直接传播到O点。现在已知玻璃片的厚度为d,玻璃对该光的折射率为1.5,真空中的光速为c,不计光在玻璃片内、外的反射。下列判断正确的是________。
A.若玻璃片的厚度d=15λ,则O点处为亮条纹
B.若单缝S略微向左移动(经S1出射后仍可垂直穿过玻璃片),则原O点位置处的条纹位置不变
C.若单缝S略微向下移动(经S出射后仍可垂直穿过玻璃片),则原O点位置处的条纹也略微向下移动
D.若用该波长的光完成实验,O点处为亮条纹,保持其他条件不变的情况下,用另一种波长的光实验,O点处也一定为亮条纹
5.(2023·浙江杭州市长征中学期中)用普通小灯泡作为光源完成“用双缝干涉测量光的波长”实验,首先将实验仪器按图甲所示的方式安装在光具座上。
(1)下列做法,有助于减小实验误差的是______;
A.将单缝拆下
B.将单缝与双缝的位置互换
C.增大单缝与双缝间的距离
D.一次测出多条亮条纹间的距离,再算出相邻亮条纹的间距
(2)某同学选用红色滤光片进行测量,使测量头分划板中心刻线与某一亮条纹A的中心对齐,此时测量头上的游标卡尺如图乙所示(图乙为50分度游标卡尺),其读数x1=________ mm。然后转动手轮,使分划板中心刻线与另一亮条纹B的中心对齐,此时游标卡尺的读数为x2(x2>x1),已知亮条纹A、B间还有4条亮条纹,则相邻亮条纹的间距为________(用x1和x2表示);
(3)若相邻亮条纹的间距记为Δx,双缝间距、屏与双缝间的距离分别记为d和l,则测量得到的单色光波长λ=________(用Δx、d和l表示)。
6.洛埃德在1834年提出了一种更简单的观察干涉的装置。如图所示,单色光从单缝S射出,一部分入射到平面镜后反射到光屏上,另一部分直接投射到屏上,在屏上两光束交叠区域里将出现干涉条纹。单缝S通过平面镜成的像是S′。
(1)通过洛埃德镜在屏上可以观察到明暗相间的干涉条纹,这和双缝干涉实验得到的干涉条纹一致。如果S被视为其中的一个缝,________相当于另一个“缝”;
(2)实验中已知单缝S到平面镜的垂直距离h=0.15 mm,单缝到光屏的距离D=1.2 m,观测到第3个亮条纹中心到第12个亮条纹中心的间距为22.78 mm,则该单色光的波长λ=________ m(结果保留3位有效数字);
(3)下列能够增大光屏上相邻两条亮纹之间的距离的操作是________;
A.将平面镜稍向上移动一些
B.将平面镜稍向右移动一些
C.将光源由红色光改为绿色光
(4)实验表明,光从光疏介质射向光密介质界面发生反射,在入射角接近90°时,反射光与入射光相比,相位有π的变化,称为“半波损失”。如果把光屏移动到和平面镜接触,接触点P处是________。(选填“亮条纹”或“暗条纹”)
4 实验:用双缝干涉测量光的波长
1.(1)②靠近 (2)C
解析 (1)②若增加从目镜中观察到的条纹个数,则条纹间距应减小,根据Δx=λ可知需将毛玻璃屏向靠近双缝的方向移动。
(2)条纹间距指的是相邻两条亮条纹的中心线间的距离或者相邻两条暗条纹的中心线间的距离,故选C。
2.(1)AC (2)6.50×10-7
解析 (1)相邻两亮条纹间距Δx=λ,蓝光波长小于红光波长,将蓝色滤光片换成红色滤光片,则干涉条纹间距变宽,故A正确;条纹间距与单缝和双缝间的距离无关,故B错误;双缝间距变大,条纹间距变小,故C正确;光源发出的光如果不是单色光,去掉滤光片,仍能发生干涉现象,是复色光的干涉,故D错误。
(2)条纹间距Δx==0.26 mm
双缝与屏之间的距离为L=0.80 m,双缝间的距离d=2 mm,
由Δx=λ得λ=,
代入数据得λ=6.50×10-7 m。
3.(1)C (2)
解析 (1)实验中所得到的干涉条纹与双缝平行,故A错误;由Δx=λ可知,干涉条件的疏密程度与双缝间的距离、双缝到屏的距离以及光的波长有关,故C正确,B错误。
(2)由题意可知,相邻亮条纹间的距离为Δx=,又Δx=λ,解得λ=。
4.(1)平行 (2)1.05 (3)B
解析 (1)只有保证单缝和双缝互相平行,才能在屏上出现明暗相间的条纹。
(2)游标尺为10分度,主尺读数为10 mm,游标尺上第5条刻度线与主尺上的刻度线对齐,故读数为10 mm+5×0.1 mm=10.5 mm=1.05 cm。
(3)光在玻璃中传播时对应的路程为l′=c·=nd,S1、S2到O点的路程差为Δl=l′-d=nd-d=λ,
可知,S1、S2到O点的路程差为半波长的奇数倍,故O点处为暗条纹,故A错误;
单缝向左移动,改变了单缝到双缝的距离,不会影响光经过双缝后的传播情况,故屏上的条纹分布情况不变,故B正确;
若单缝S略微向下移动,则主光轴逆时针倾斜,则原O点位置处的条纹略微向上移动,故C错误;
O点处为亮条纹或暗条纹,与玻璃片的厚度,光的波长都有关系,所以用该波长的光完成实验,O点处为亮条纹,保持其他条件不变的情况下,用另一种波长的光实验,O点处可能为亮条纹,也可能为暗条纹,故D错误。
5.(1)D (2)10.36 (3)Δx
解析 (1)将单缝拆下或将单缝与双缝的位置互换,则无法获得干涉图样,实验无法完成,故A、B错误;增大单缝与双缝间的距离,对实验结果没有影响,故C错误;一次测出多条亮条纹间的距离,再算出相邻亮条纹的间距,这样有助于减小实验误差,故D正确。
(2)由题图乙知,50分度游标卡尺的读数为x1=(10+18×0.02) mm=10.36 mm;已知亮条纹A、B间还有4条亮条纹,则相邻亮条纹的间距为Δx=。
(3)由干涉条纹的间距公式Δx=λ知,测量得到的单色光波长λ=Δx。
6.(1)S′ (2)6.33×10-7 (3)A (4)暗条纹
解析 (1)通过洛埃德镜在屏上可以观察到明暗相间的干涉条纹,这和双缝干涉实验得到的干涉条纹一致。如果S被视为其中的一个缝,S′相当于另一个“缝”。
(2)第3个亮条纹中心到第12个亮条纹中心的间距为22.78 mm,
则相邻亮条纹间距为Δx= m≈2.53×10-3 m
等效双缝间的距离为d=2h=0.30 mm=3.0×10-4 m
根据双缝干涉条纹间距公式有Δx=λ
则有λ== m≈6.33×10-7 m。
(3)根据Δx=λ可知,仅增大D,仅减小d,仅增大波长λ,能够增大光屏上相邻两条亮条纹之间的距离,所以A正确,B、C错误。
(4)如果把光屏移动到和平面镜接触,在入射角接近90°时,反射光与入射光相比,相位有π的变化,即“半波损失”,故直接射到光屏上的光和经平面镜反射的光相位差为π,所以接触点P处是暗条纹。
