勾股定理的应用
图片预览



文档简介
课件16张PPT。
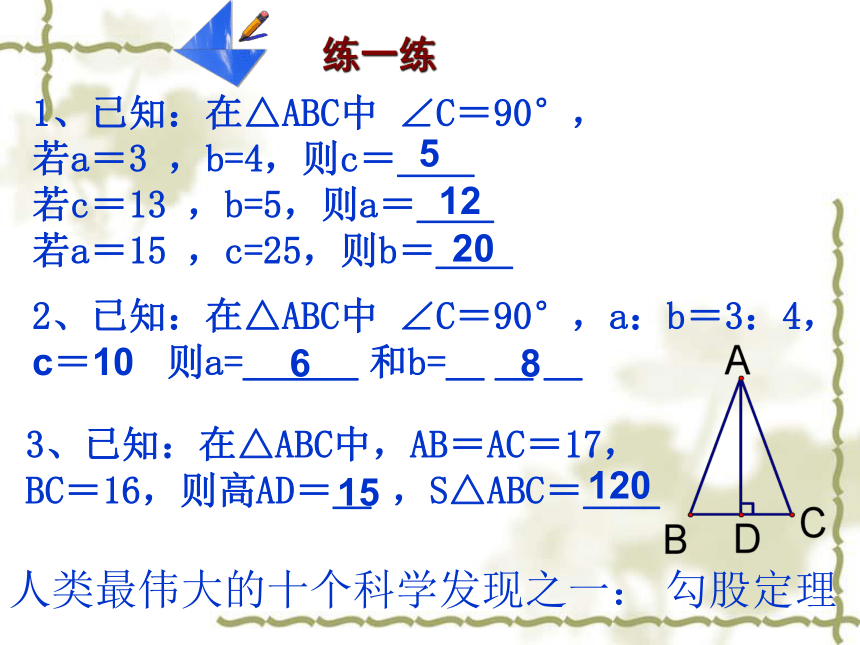
热烈欢迎各位老师莅临指导勾股定理的应用2、已知:在△ABC中 ∠C=90°,a:b=3:4, c=10 则a=___ 和b=_ _ _ 3、已知:在△ABC中,AB=AC=17, BC=16,则高AD=_ ,S△ABC=__人类最伟大的十个科学发现之一:?勾股定理68120151、已知:在△ABC中 ∠C=90°, 若a=3 ,b=4,则c=__ 若c=13 ,b=5,则a=__ 若a=15 ,c=25,则b=__12205
图片赏析美丽的勾股树
把勾股定理送到外星球,与外星人进行数学交流 !
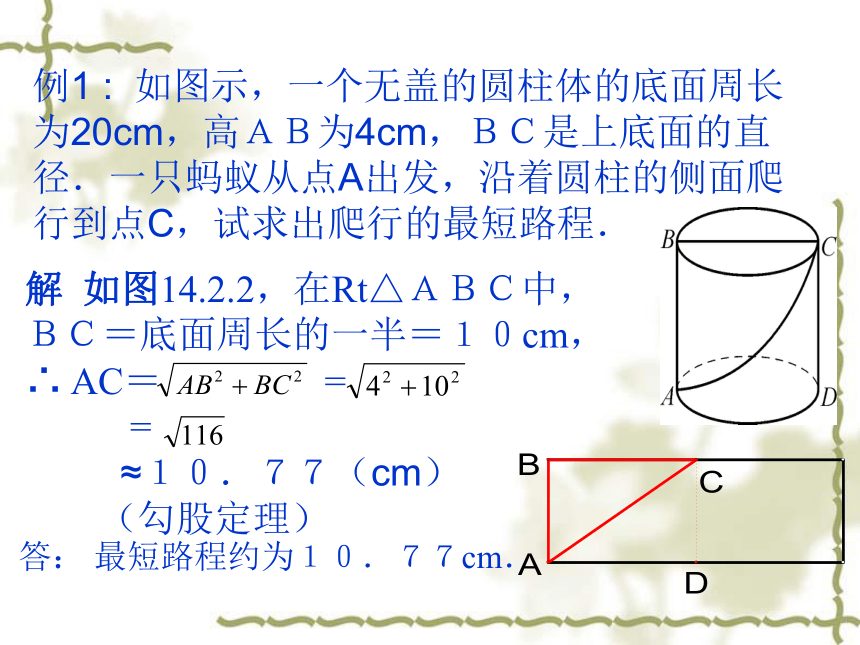
——华罗庚例1 : 如图示,一个无盖的圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. 解 如图14.2.2,在Rt△ABC中,
BC=底面周长的一半=10cm,
∴ AC= =
=
≈10.77(cm)
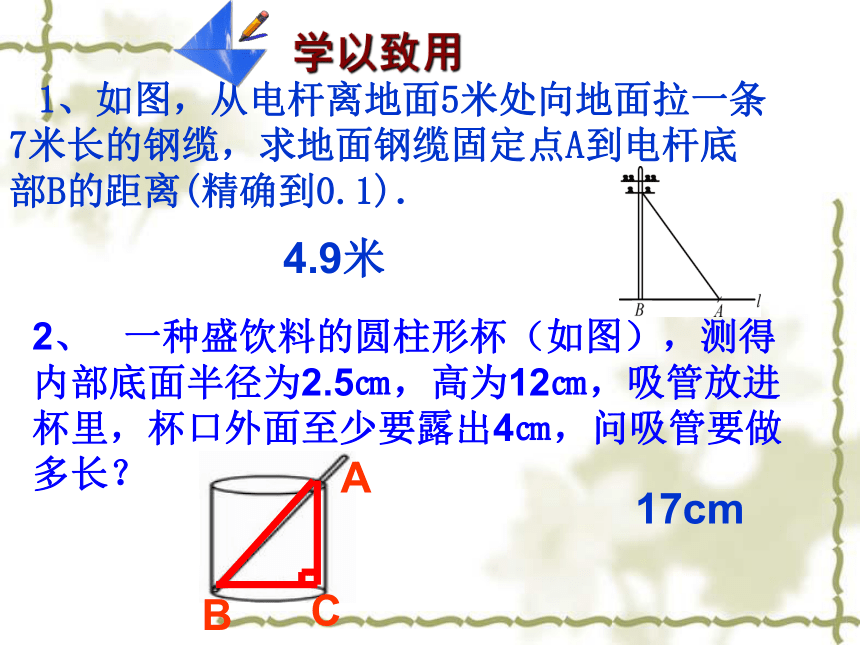
(勾股定理)答: 最短路程约为10.77cm.1、如图,从电杆离地面5米处向地面拉一条7米长的钢缆,求地面钢缆固定点A到电杆底部B的距离(精确到0.1).2、 一种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4㎝,问吸管要做多长? 4.9米17cm 例2、如图是一个正方体盒子,在正方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少?ABBACD注意:1、没有图的要按题意画好图并标上字母;
2、要善于发现、构造直角三角形,正确利用定理解题。拓展提高3、现准备将一块形为直角三角形的绿地扩大,使其仍为直角三角形,两直角边同时扩大到原来的两倍,问斜边扩大到原来的多少倍? 2倍 4、如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 ( )
A.7m B.8m C.9m D.10m8m8m2mD做一做1、如图14.2.4,以直角三角形ABC的三边为边分别向外作正方形,其中一个正方形划分成四个形状与大小都一样的四边形.试将图中5个带色的图形拼入到大正方形中,填满整个大正方形.探索活动这节课,我的收获是--- 小结:直角三角形在实际生活中有更为广泛的应用希望同学们能紧紧抓住直角三角形的性质,学透勾股定理的具体应用,那样就能很轻松的解决现实生活中的许多问题,达到事半功倍的效果。通过这节课的学习,想想勾股定理的应用有那些方面?小结与回顾 1、在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC思考题 演示x+1BCAH15?┓x解:设水池的水深AC为x尺,则这根芦苇长AD=AB=(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得,BC2+AC2=AB2即 52+ x2= (x+1)225+ x2= x2+2 x+1,2 x=24,∴ x=12, x+1=13答:水池的水深12尺,
这根芦苇长13尺。生活中的数学无处不在
希望同学们善于
用数学的视角观察世界
用数学的思维理解世界
发现生活中的数学
惊奇和趣味也许就在我们身边!共勉例2 :一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状(如图示)的某工厂,问这辆卡车能否通过该工厂的厂门?解:在Rt△OCD中,由勾股定理得
CD= =
=0.6CH=0.6+2.3=2.9>2.5
因此高度上有0.4米的余量,
所以卡车能通过厂门
再见!
热烈欢迎各位老师莅临指导勾股定理的应用2、已知:在△ABC中 ∠C=90°,a:b=3:4, c=10 则a=___ 和b=_ _ _ 3、已知:在△ABC中,AB=AC=17, BC=16,则高AD=_ ,S△ABC=__人类最伟大的十个科学发现之一:?勾股定理68120151、已知:在△ABC中 ∠C=90°, 若a=3 ,b=4,则c=__ 若c=13 ,b=5,则a=__ 若a=15 ,c=25,则b=__12205
图片赏析美丽的勾股树
把勾股定理送到外星球,与外星人进行数学交流 !
——华罗庚例1 : 如图示,一个无盖的圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. 解 如图14.2.2,在Rt△ABC中,
BC=底面周长的一半=10cm,
∴ AC= =
=
≈10.77(cm)
(勾股定理)答: 最短路程约为10.77cm.1、如图,从电杆离地面5米处向地面拉一条7米长的钢缆,求地面钢缆固定点A到电杆底部B的距离(精确到0.1).2、 一种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4㎝,问吸管要做多长? 4.9米17cm 例2、如图是一个正方体盒子,在正方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少?ABBACD注意:1、没有图的要按题意画好图并标上字母;
2、要善于发现、构造直角三角形,正确利用定理解题。拓展提高3、现准备将一块形为直角三角形的绿地扩大,使其仍为直角三角形,两直角边同时扩大到原来的两倍,问斜边扩大到原来的多少倍? 2倍 4、如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 ( )
A.7m B.8m C.9m D.10m8m8m2mD做一做1、如图14.2.4,以直角三角形ABC的三边为边分别向外作正方形,其中一个正方形划分成四个形状与大小都一样的四边形.试将图中5个带色的图形拼入到大正方形中,填满整个大正方形.探索活动这节课,我的收获是--- 小结:直角三角形在实际生活中有更为广泛的应用希望同学们能紧紧抓住直角三角形的性质,学透勾股定理的具体应用,那样就能很轻松的解决现实生活中的许多问题,达到事半功倍的效果。通过这节课的学习,想想勾股定理的应用有那些方面?小结与回顾 1、在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC思考题 演示x+1BCAH15?┓x解:设水池的水深AC为x尺,则这根芦苇长AD=AB=(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得,BC2+AC2=AB2即 52+ x2= (x+1)225+ x2= x2+2 x+1,2 x=24,∴ x=12, x+1=13答:水池的水深12尺,
这根芦苇长13尺。生活中的数学无处不在
希望同学们善于
用数学的视角观察世界
用数学的思维理解世界
发现生活中的数学
惊奇和趣味也许就在我们身边!共勉例2 :一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状(如图示)的某工厂,问这辆卡车能否通过该工厂的厂门?解:在Rt△OCD中,由勾股定理得
CD= =
=0.6CH=0.6+2.3=2.9>2.5
因此高度上有0.4米的余量,
所以卡车能通过厂门
再见!
