24.2.2 直线和圆的位置关系(3)学案(无答案)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系(3)学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 68.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 10:43:28 | ||
图片预览


文档简介
24.2.2 直线和圆的位置关系(3)
学习目标:
【知识与技能】
1、掌握切线长的概念及切线长定理
2、掌握三角形的内切圆及内心等概念
3、会作三角形的内切圆
【过程与方法】
1、 利用圆的轴对称性帮助探索切线长的特征
2、 结合求三角形内面积最大的圆的问题,给出了三角形的内切圆和内心的概念
3、 类比思想、数形结合、方程思想的运用
【情感、态度与价值观】
通过操作、实验、发现、证明等数学活动,探索数学结论,激发学生学习数学的兴趣
【重点】
切线长定理
【难点】
内切圆、内心的概念及运用
学习过程:
一、自主学习
(一)复习巩固
1、三角形的外心:
2、角平分线的性质定理:
3、切线的判定定理:
4、切线的性质定理:
(二)自主探究
1、按探究要求,请同学们动手操作,思考24.2—12中, OB是⊙O的一条半径吗?PB是⊙O的切线吗? 利用图形的轴对称性,说明圆中的PA与PB,∠APO与∠BPO有什么关系?
__________________________________________
2、什么叫切线长
注意:切线和切线长是两个不同的概念,切线是 ,不能度量;切线长是 的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
3、切线长定理:
从圆外一点可以引圆的两条 ,它们的切线长 ,这一点和圆心
的连线 两条切线的 .
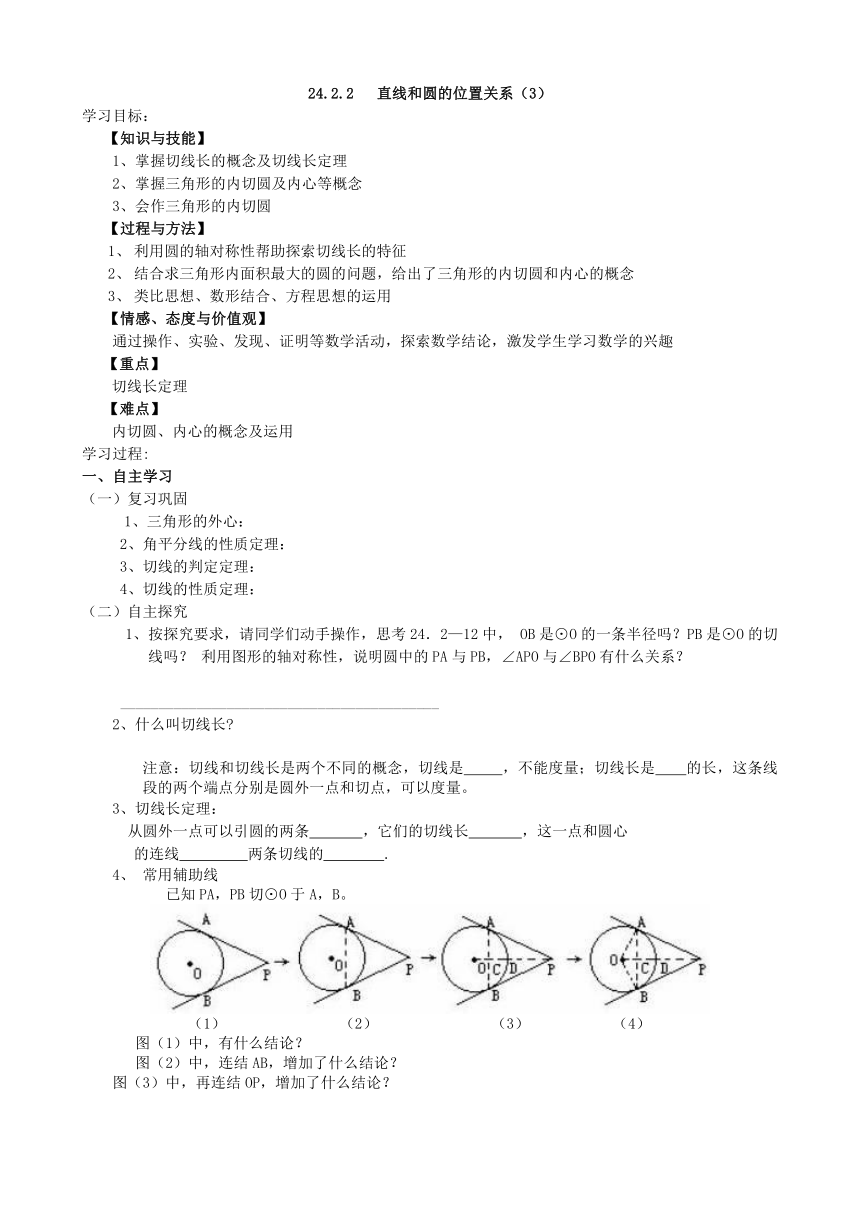
4、 常用辅助线
已知PA,PB切⊙O于A,B。
(1) (2) (3) (4)
图(1)中,有什么结论?
图(2)中,连结AB,增加了什么结论?
图(3)中,再连结OP,增加了什么结论?
图(4)中,再连结OA,OB。又增加了什么结论?
5、 和三角形的各边都相切的圆
与三角形各边都 的圆叫做三角形的内切圆,内切圆的圆心是三角形三条 的交点,叫做三角形的内心。
注意:“接”与“切”是说明三角形顶点和边与圆的关系,顶点都在圆上的叫做“接”,各边都与圆相切的叫做“切”。
(三)、归纳总结:
1、圆的切线长概念
2、切线长定理
3、三角形的内切圆及内心的概念
(四)自我尝试:
1、如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知PA=7cm,则△PCD的周长等于_________.
2、如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AB=2,BC=3,AC=1,且△ABC的面积为6.求内切圆的半径r.(提示:内心为O,连接OA,OB,OC)
3、当 △ABC的内切圆的半径r, △ABC的周长为L,求△ABC的面积
二、教师点拔
1、切线长是一条 长,是经过圆外一点向圆作的 ,这一点与切点间的线段
的长度。而切线是 ,不能度量它的长度。我们不能说两切线相等,而应该说
两 相等。
2、作三角形的内切圆,关键是找圆心的位置和确定圆的半径大小,圆心就是三角形 ,而半径等于这个交点到三角形 的距离,由此可见,任何一个三角形 内切圆,而一个圆有 个外切三角形。
三、课堂检测
1、如图3,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则
∠AOB=_________.
(3) (4)
2、Rt在△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆的半径r=_________.
3、如图4,圆O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是_______.
四、课外训练
1、如图所示,PA、PB是⊙O的两条切线,A、B为切点,
求证:∠ABO=∠APB.
2.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则
∠APB=( )
A.180°-a B.90°-a C.90°+a D.180°-2a
3.如图3,边长为a的正三角形的内切圆半径是_________.
4、如下图所示,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果
∠E=46°,∠DCF=32°,求∠A的度数.
5、如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=2,BF=3,且
△ABC的面积为6.求内切圆的半径r.(提示:内心为O,连接OA,OB,OC)
6、 如图,△ABC中,∠A=α°,O是△ABC的内心。求证:
学习目标:
【知识与技能】
1、掌握切线长的概念及切线长定理
2、掌握三角形的内切圆及内心等概念
3、会作三角形的内切圆
【过程与方法】
1、 利用圆的轴对称性帮助探索切线长的特征
2、 结合求三角形内面积最大的圆的问题,给出了三角形的内切圆和内心的概念
3、 类比思想、数形结合、方程思想的运用
【情感、态度与价值观】
通过操作、实验、发现、证明等数学活动,探索数学结论,激发学生学习数学的兴趣
【重点】
切线长定理
【难点】
内切圆、内心的概念及运用
学习过程:
一、自主学习
(一)复习巩固
1、三角形的外心:
2、角平分线的性质定理:
3、切线的判定定理:
4、切线的性质定理:
(二)自主探究
1、按探究要求,请同学们动手操作,思考24.2—12中, OB是⊙O的一条半径吗?PB是⊙O的切线吗? 利用图形的轴对称性,说明圆中的PA与PB,∠APO与∠BPO有什么关系?
__________________________________________
2、什么叫切线长
注意:切线和切线长是两个不同的概念,切线是 ,不能度量;切线长是 的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
3、切线长定理:
从圆外一点可以引圆的两条 ,它们的切线长 ,这一点和圆心
的连线 两条切线的 .
4、 常用辅助线
已知PA,PB切⊙O于A,B。
(1) (2) (3) (4)
图(1)中,有什么结论?
图(2)中,连结AB,增加了什么结论?
图(3)中,再连结OP,增加了什么结论?
图(4)中,再连结OA,OB。又增加了什么结论?
5、 和三角形的各边都相切的圆
与三角形各边都 的圆叫做三角形的内切圆,内切圆的圆心是三角形三条 的交点,叫做三角形的内心。
注意:“接”与“切”是说明三角形顶点和边与圆的关系,顶点都在圆上的叫做“接”,各边都与圆相切的叫做“切”。
(三)、归纳总结:
1、圆的切线长概念
2、切线长定理
3、三角形的内切圆及内心的概念
(四)自我尝试:
1、如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知PA=7cm,则△PCD的周长等于_________.
2、如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AB=2,BC=3,AC=1,且△ABC的面积为6.求内切圆的半径r.(提示:内心为O,连接OA,OB,OC)
3、当 △ABC的内切圆的半径r, △ABC的周长为L,求△ABC的面积
二、教师点拔
1、切线长是一条 长,是经过圆外一点向圆作的 ,这一点与切点间的线段
的长度。而切线是 ,不能度量它的长度。我们不能说两切线相等,而应该说
两 相等。
2、作三角形的内切圆,关键是找圆心的位置和确定圆的半径大小,圆心就是三角形 ,而半径等于这个交点到三角形 的距离,由此可见,任何一个三角形 内切圆,而一个圆有 个外切三角形。
三、课堂检测
1、如图3,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则
∠AOB=_________.
(3) (4)
2、Rt在△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆的半径r=_________.
3、如图4,圆O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是_______.
四、课外训练
1、如图所示,PA、PB是⊙O的两条切线,A、B为切点,
求证:∠ABO=∠APB.
2.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则
∠APB=( )
A.180°-a B.90°-a C.90°+a D.180°-2a
3.如图3,边长为a的正三角形的内切圆半径是_________.
4、如下图所示,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果
∠E=46°,∠DCF=32°,求∠A的度数.
5、如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=2,BF=3,且
△ABC的面积为6.求内切圆的半径r.(提示:内心为O,连接OA,OB,OC)
6、 如图,△ABC中,∠A=α°,O是△ABC的内心。求证:
同课章节目录
